Question

In Fig. coil $1$ and coil $2$ are wound on a long cylindrical insulator. The ends $A\text{'}$ and $B$ are joined together and current $I$ is passed. Self-inductance of the two coils are $L_1$ and $L_2$, and their mutual inductance is $M$.
a. Show that this combination can be replaced by a single coil of equivalent inductange given by
$L_{eq}=L_1+L_2+2M$.
b. How could the coils be reconnected by yieldings an equivalent inductance of $L_{eq}=L_1+L_2-2M$.

Explanation

When the termial `A`' and `B` are connected, the sence of current in both the coil is same. Let the current be changing at the rate of `dI//dt`. The magnetic fields of both coil `1` and coil `2` point toward left. When the current increases, both fields increases and both the changes in flux contribute emfs in the same direction. Thus, the induced emf in coil `1` is
`E_(1) = - (L_(1) + M) (dI)/(dt)` (i)
Similarly, the magnetic field in coil `2` due to it and field due to coil `1` point toward left. The two induced emfs are again in the same direction.
`E_(2) = - (L_(2) + M) (dI)/(dt)` (ii)
Hence, the total emf across both the coils is
`E = E_(1) + E_(2) = - (L_(1) + L_(2) + 2M)(dI)/(dt)` (iii)
If these coils were replaced by a single coil, then we have
`E = - L_(eq) (dI)/(dt)` (iv)
On comparing Eqs (iii) and (iv), we have
`L_(eq) = L_(1) + L_(2) + 2M`

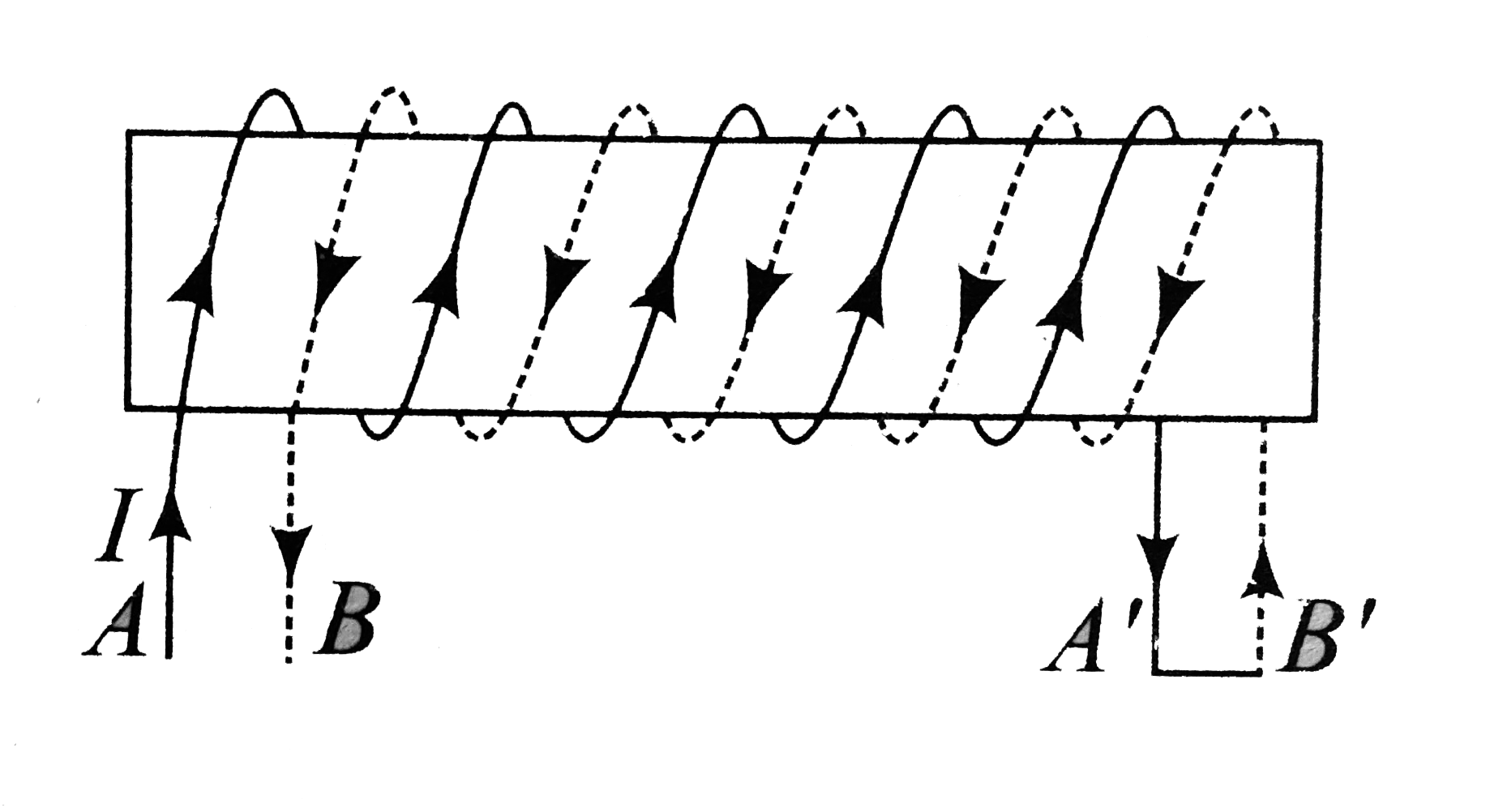
b.When terminals `A'` and `B` are connected, the sense of the flow of current in coil `1` is opposite to that in coil `2`. Then at the site of coil `1` the field produced by coil `2`is opposite to the field produced by coil 1 itself. An increasing current in coil 1 tends to increase the flux in that coil but an increasing current on coil 2 tends to decrease it. The emf across coil 1 is
`E_(1) = - (L_(1) - M) (dI)/(dt)`
Similarly, emf across coil 2 is `E_(2) = - (L_(2) - M) (dI)/(dt)`.
The total emf `E = E_(1) + E_(2) = - (L_(1) + L_(2) - 2 M) (dI)/(dt)`
Thus, `L_(eq) = (L_(1) + L_(2) - 2M)`