Two conducting circular loops of radii R1andR2 are placed in the same plane with their centres coincidingt. Find the mutual inductane between them assuming R2<<R1.
R1R2
R2R1
R21R2
R22R1
The correct Answer is:D
Let a current I1 flows through the outer circular coil of radius R1.
The magnetic field at the centre of the coil is B =μ0I12R1
As the inner coil of radius R2 placed co-axially has small radius (R2<R1) , therefore B1 may be taken constant over its crosssectional area. Hence, flux associated with the inner coil is
ϕ2=B1πR22=μ0I12R1πR22
As M=ϕ2I1=μ0πR222R1∴M∝R22R1
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTSBOOK - MTG GUIDECHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTSEXERCISE - NEET CAFE TOPICWISE PRATICE QUESTIONS (INSTANTANEOUS, AVERAGE AND RMS VALUE OF ALTERNATING CURRENT/ VOLTAGE)
5 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTSBOOK - MTG GUIDECHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTSEXERCISE - NEET CAFE TOPICWISE PRATICE QUESTIONS (AC CIRCUITS CONTAINING RESISTOR, INDUCTOR OR CAPACITOR)
3 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTSBOOK - MTG GUIDECHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTSEXERCISE - NEET CAFE TOPICWISE PRATICE QUESTIONS (LENZ.S LAW)
1 Videos
- DUAL NATURE OF MATTER AND RADIATION BOOK - MTG GUIDECHAPTER - DUAL NATURE OF MATTER AND RADIATION EXERCISE - AIPMT/ NEET MCQs
30 Videos
- ELECTROMAGNETIC WAVESBOOK - MTG GUIDECHAPTER - ELECTROMAGNETIC WAVESEXERCISE - AIPMT/NEET(MCQs)
15 Videos
Similar Questions
Two conducting circular loops of radii R1 and R2 are placed in the same plane with their centres coinciding. If R1 >> R2 the mutual inductance M between them will be directly proportional to
View SolutionTwo concentric circular coil,s one of small radius r1 and the other of large radius r2, such that r1<<r2, are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
View Solution
Knowledge Check
Two concentric co - planar circular loops of radius R and r(<<R) are placed as shown in the figure. The mutual inductance of the system will be
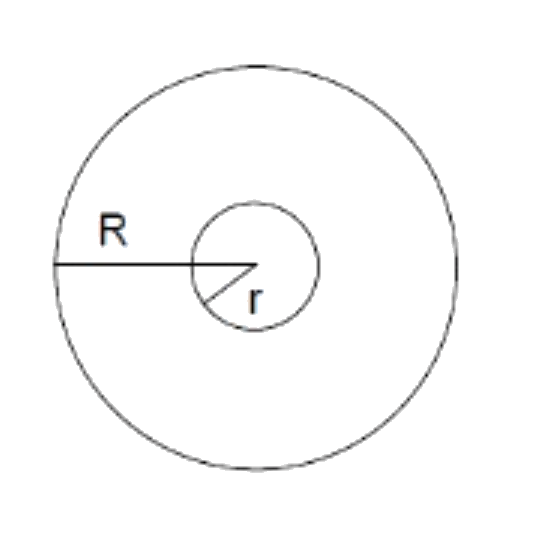 Aπμ0r22RBπμ0r24RCπμ0R24rDπμ0R22r
Aπμ0r22RBπμ0r24RCπμ0R24rDπμ0R22rTwo conducting spheres of radii r1 and r2 are equally charged. The ratio of their potentral is-
Ar21/r22Br22/r21Cr1/r2Dr2/r1Two concentric circular coils, one of small radius r1and the other of large radiusr2 such that r1<<r2 are placed coaxially with centres coinciding. Obtain the mutual inductance of the arrangement.
Aμ0πtr212r2Bμ0πtr222r1Cμ0πtr22r1Dμ0πtr21r2
Two concentric circular coils of radius r and R are placed coaxially with centres coinciding If R>>r then calculate the mutual inductance the coils.
View SolutionTwo coils are placed closed to each other. The mutual inductance between them assuming R2<<R1
View SolutionTwo circular loops of radius r and R (R>>r) are placed coaxially with their centres coinciding. What will be the mutual inductance for the pair? If one of the coils is rotated through 90∘ angle, then what will be the new mutual inductance?
View SolutionTwo circular coils, one of smaller radius r1 and the other of very large radius r2 are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
View SolutionA coil of radius r is placed at the centre of R>>r and coils are in same plane.The coefficient of mutual inductance between the coil is
View Solution
