Two cubes with masses m1 and m2 were interconnected by a weightless spring of stiffness x and placed on a smooth horizontal surface. Then the cubes were drawn closer to each other and released simultaneously. Find the natural oscillation frequency of the system.
In the C.M. frame ( which is rigidly attached with the centre of mass of the two cubres ) the cubes oscillates. We know that the kinetic energy of two body system equals 12μv2rel, where μ is the reduced mass and vrel is the modulus of velocity of any one body particle relative to other . From the conservation of mechanical energy of the oscialltion :
12kx2+12μ{ddt(l0+x)}2= constant
Here l0 is the natural length of the spring.
Differenting the above equation w.r.t. time, we get :
12k2x.x+12μ2.x..x=0[ becomesd(l0+x)dt=.x]
Thus ..x=−kμx(whereμ=m1m2m1+m2)
Hence the natural frequency of oscillation :ω0=√kμwhereμ=m1m2m1+m2
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electric Oscillations
56 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
Two cubes of mass m1 and m2 are interconnected by a weightless spring of stiffness k and placed on a smooth horizontal table. Then the cubes are drawn closer to each other and released. Find the frequency of oscillation.

View SolutionTwo blocks of masses m1andm2 being connected with a light spring of stiffness k are driven with forces F1andF2 on a smooth horizontal plane.
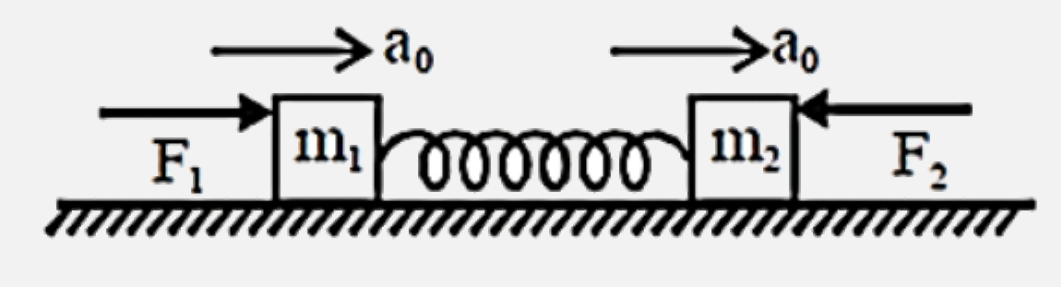
View Solution
Knowledge Check
Two blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
Athe momentum of each particle remains constant separatelyBthe magnitude of momentums of each body are equal to each otherCthe mechanical energy of system remains constantDboth (C) and (B) are correctTwo bars of masses m1 and m2 connected by a weightless spring of stiffness k, rest on a smooth horizontal plane. Bar 2 is shifted by a small distance x0 to the left and released. The veloicyt of the centre of mass of the system when bar 1 breaks off the wall is
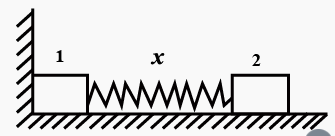 A(a) x0√km2m1+m2B(b) x0m1+m2√km2C(c) x0km1+m2m2D(d) x0√km1(m1+m2)
A(a) x0√km2m1+m2B(b) x0m1+m2√km2C(c) x0km1+m2m2D(d) x0√km1(m1+m2)
Two blocks of masses m1 and m2, connected by a weightless spring of stiffness k rest on a smooth horizontal plane as shown in Fig. Block 2 is shifted a small distance x to the left and then released. Find the velocity of centre of mass of the system after block 1 breaks off the wall.

View SolutionTwo bars of masses m1 and m2 connected by a weightless spring of stiffness ϰ (figure) rest on a smooth horizontal plane.

Bar 2 is shifted a small distance x to the left and then released. Find the velocity of the centre of inertia of the system after bar 1 breaks off the wall.
View SolutionTwo blocks A and B of masses m and 2m respectively are connected together by a light spring of stiffness k and then placed on a smooth horizontal surface. The blocks are pushed towards each other such that spring gets compressed by a length x0 and then released from rest. Find the work done on the block A by the spring, by the time the spring acquires its natural length.
View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View SolutionTwo bolcks A & B are connected by a spring of stiffness 512N/m and placed on a smooth horizontal surface. Initially the spring has its equilibrium length. The indicated velocities are imparted to A & B. Find the maximum extension in the spring?
View SolutionTwo blocks of masses m1 and m2 interconnect with a spring of stiffness K, are kept on as smooth horizontal surface. Find out the ratio of velocity, displacement, kinetic energy and acceleration block with mass m1 of block with mass m2.
View Solution
