Two discs A and B are moving with their flat circular surface on a smooth horizontal surface. Mass, radius and velocity of the two discs are −mA=2M,mB=M,rA=R,=2R,vA=v, and vB=2v. The velocities of the two discs are oppositely directed so that they just cannot avoid collision and stick to each other (see figure)
(a) Find the angular speed of the composite system after collision
(b) Find loss in kinetic energy due to collision
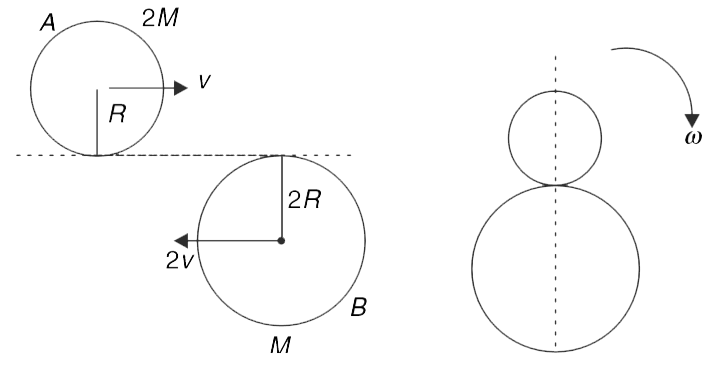
The correct Answer is:(a) ω=2v3R
(b) kEloss=Mv2
Step by step video, text & image solution for Two discs A and B are moving with their flat circular surface on a smooth horizontal surface. Mass, radius and velocity of the two discs are - m_(A) = 2M, m_(B) = M, r_(A) = R, = 2R, v_(A) = v, and v_(B) = 2v. The velocities of the two discs are oppositely directed so that they just cannot avoid collision and stick to each other (see figure) (a) Find the angular speed of the composite system after collision (b) Find loss in kinetic energy due to collision by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
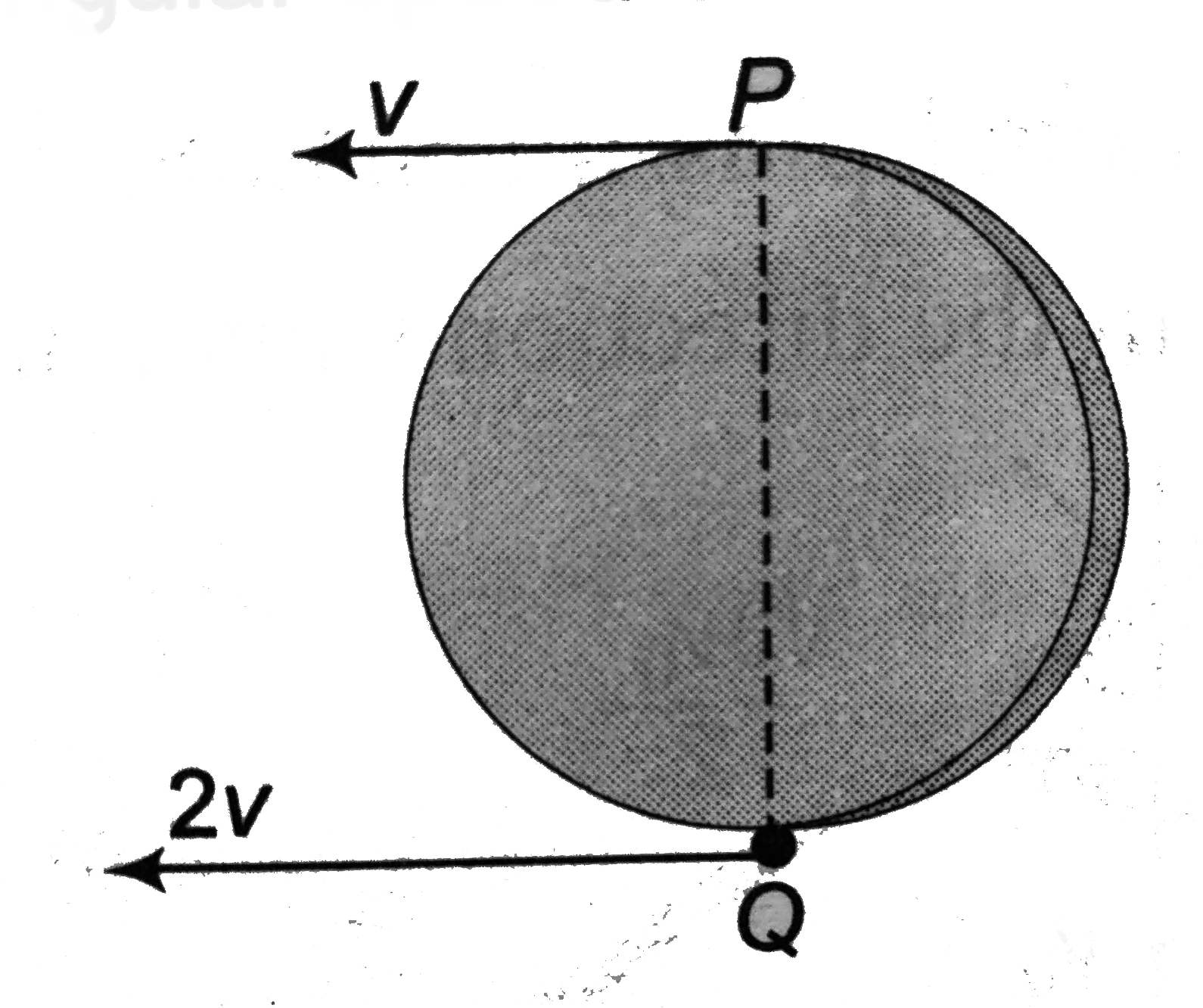
Two point P and Q. diametrically opposite on a disc of radius R have linear velocities v and 2v as shown in figure. Find the angular speed of the disc.View SolutionA uniform circular disc of mass m is set rolling on a smooth horizontal table with a uniform linear velocity v. Find the total K.E. of the disc.
View Solution
Knowledge Check
- Question 1 - Select One
Two particle of masses m and 2m are coliding elastically as given in figure. If V1 and V2 speed of particle just after collision then
_2019_CBT5_E01_051_Q01.png)
AV1=11.16m/s,V2=6.31m/sBV1=10.16m/s,V2=5.31m/sCv1=9.16M/S,v2=6.31M/SDv1=6.31M/S,v2=11.16M/S - Question 2 - Select One
A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0 - Question 3 - Select One
Two masses m, and m, moving with velocities vaandvb in opposite direction collide elastically and after the collision maandmb move with velocities vbandva respectively. Then the ratio mamb is
A(va−vbva+vb)Bva+vbva+vbC1D12
A uniform disc of mass m, radius R is placed on a smooth horizontal surface. If we apply a horizontal force F at P as shown in the figure. If F=4N,m=.1kg,R=1m and r=12m then, find the:
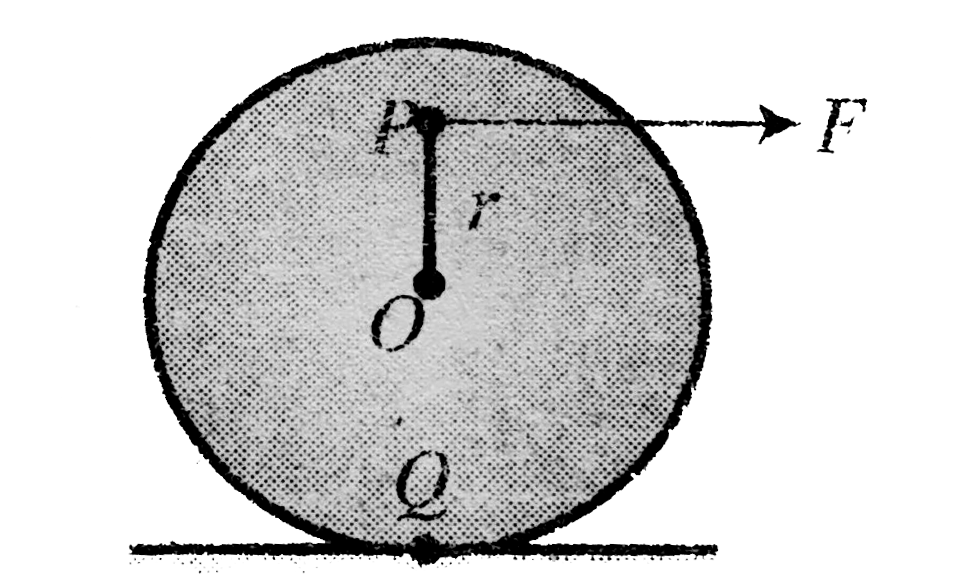
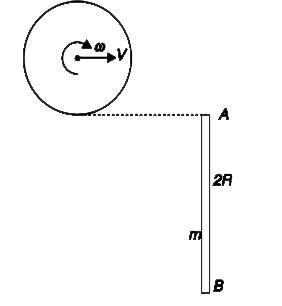
angular acceleration of the disc. (rads−1)View SolutionA disc of mass m and radius R is moving on a smooth horizontal surface with the flat circular face on the surface. It is spinning about its centre with angular peed ω and has a velocity V (see figure). It just manages to hit a stick AB at its end A. The stick was lying free on the surface and stick to the disc. [The combined object becomes like a badminton racket]. Mass and length of the stick are m and 2R respectively.
(a) Calculate the angular speed of the combined object assuming V=Rω
(b) Calculate loss in kinetic energy. Why is energy lost ?
(c) If V=η(Rω), loss in kinetic energy is minimum. Find η. (Assume ω is given]
View SolutionTwo balls of masses m and 2m moving in opposite directions collide head on elastically with velocities v and 2v. Find their velocities after collision.
View SolutionA disc of mass m is moving with constant speed v0 on a smooth horizontal table. Another disc of mass M is placed on the table at rest as shown in the figure. If the collision is elastic, find the velocity of the disc after collision. Both disc lie on the same horizontal plane of the table.
View SolutionA disc of the radius R is confined to roll without slipping at A and B. If the plates have the velocities v and 2v as shown, the angular velocity of the disc is
View Solution