Two fat astronauts each of mass 120 kg are travelling in a closed spaceship moving at a speed of 15 km/s in the outer space far removed from tall other material objects. The total mass of the spaceship and its contents including the astronauts is 660 kg. If the astronauts do slimming exercise and thereby reduce their masses to 90 kg each, with what velocity will spaceship move?
The correct Answer is:A
To solve the problem, we will use the principle of conservation of momentum. The total momentum of a closed system remains constant if no external forces are acting on it.
1. Identify Initial Conditions:
- Mass of each astronaut before slimming: m1=120kg
- Total mass of the two astronauts: 2×m1=240kg
- Mass of the spaceship: ms=660kg−240kg=420kg
- Initial speed of the spaceship: vi=15km/s=15000m/s
2. Calculate Initial Momentum:
- Total initial mass of the system: Mi=ms+2×m1=660kg
- Initial momentum Pi of the system:
Pi=Mi×vi=660kg×15000m/s=9900000kg m/s
3. Identify Final Conditions:
- Mass of each astronaut after slimming: m2=90kg
- Total mass of the two astronauts after slimming: 2×m2=180kg
- Mass of the spaceship remains unchanged: ms=420kg
- Total final mass of the system: Mf=ms+2×m2=420kg+180kg=600kg
4. Apply Conservation of Momentum:
- According to the conservation of momentum:
Pi=Pf
- Therefore, we have:
9900000kg m/s=Mf×vf
- Where vf is the final velocity of the spaceship.
5. Solve for Final Velocity:
- Rearranging the equation gives:
vf=PiMf=9900000kg m/s600kg=16500m/s
- Converting back to km/s:
vf=16.5km/s
Final Answer:
The velocity of the spaceship after the astronauts reduce their mass will be 16.5 km/s.
- Mass of each astronaut before slimming: m1=120kg
- Total mass of the two astronauts: 2×m1=240kg
- Mass of the spaceship: ms=660kg−240kg=420kg
- Initial speed of the spaceship: vi=15km/s=15000m/s
- Total initial mass of the system: Mi=ms+2×m1=660kg
- Initial momentum Pi of the system:
Pi=Mi×vi=660kg×15000m/s=9900000kg m/s
- Mass of each astronaut after slimming: m2=90kg
- Total mass of the two astronauts after slimming: 2×m2=180kg
- Mass of the spaceship remains unchanged: ms=420kg
- Total final mass of the system: Mf=ms+2×m2=420kg+180kg=600kg
- According to the conservation of momentum:
Pi=Pf
- Therefore, we have:
9900000kg m/s=Mf×vf
- Where vf is the final velocity of the spaceship.
- Rearranging the equation gives:
vf=PiMf=9900000kg m/s600kg=16500m/s
- Converting back to km/s:
vf=16.5km/s
The velocity of the spaceship after the astronauts reduce their mass will be 16.5 km/s.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Question For short Answer
25 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -1
18 Videos
- CALORIMETRYBOOK - HC VERMA ENGLISHCHAPTER - CALORIMETRYEXERCISE - Short answer
9 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer
10 Videos
Similar Questions
Two billiard balls each of mass 0.05 kg moving in opposite directions with speed 6ms−1 collide and rebound with the same speed. What is the impulse imparted to each ball due to the other ?
View SolutionA cart A of mass 50 kg moving at a speed of 20 km/h hits a lighter cart B of mass 20 kg moving towards it at a speed of 10 km/h. The two carts cling to each other. Find the speed of the combined mass after the collision.
View Solution
Knowledge Check
Two objects, one of mass 3 kg and moving with speed of 2 m/s and the other of mass 5 kg and speed 2 m/s, move toward each other and collide head-on. If the collision is perfectly inelastic, find the speed of the object after the collision.
A0.25m/sB0.5m/sC0.75m/sD1m/s
Two objects each of mass 5 kg are moving in the same straight line but in the opposite direction towards each other with some speed of 3 m/s. They stick to each other after collision. What will be the velocity of the combined object after collision?

View SolutionTwo identical balls each of mass 4 kg are moving towards each other with speeds 2 m/s and 3 m/s respectively. They undergo head on perfectly elastic collision. Then impulse imparted by one ball on other is
View SolutionTwo masses each with mass 0.10kg are moving with velocities 3m/s along x axis and 5m/s along y-axis respectively. After an elastic collision one of the mass moves with a velocity 4ˆi+4ˆj . The energy of other mass after collision is x10 then x is
View SolutionTwo bodies of different masses 2kg and 4kg are moving with velocities 2m/s and 10m/s towards each other due to mutual gravitational attraction. Then the velocity of the centre of mass is
View SolutionTwo men to masses 80kg and 60kg are standing on a wood plank of mass 100kg, that has been placed over a smooth surface. If both the men start moving towards each other with speeds 1m/s and 2m/s respectively then find the velocity of the plank by which it starts moving.
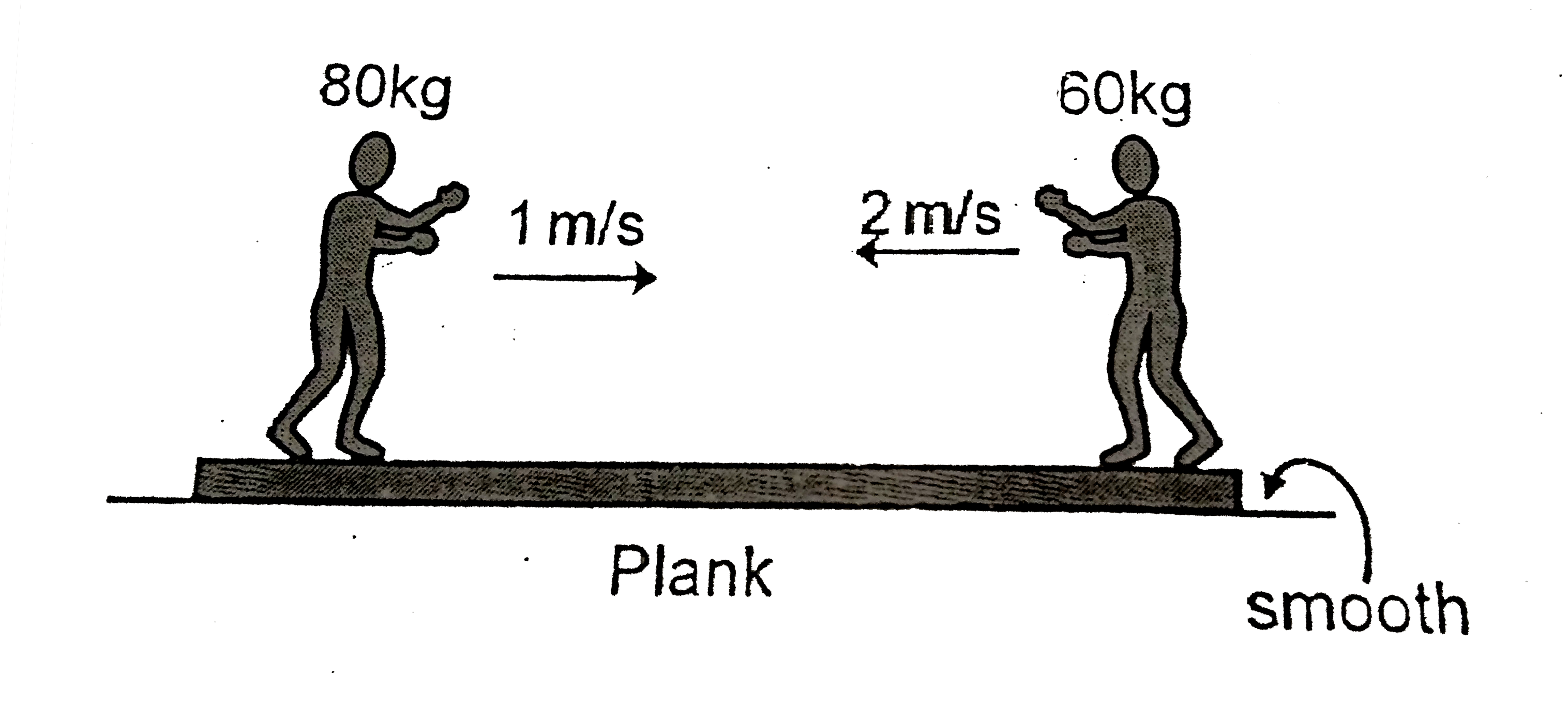
View SolutionTwo spheres of masses 4 kg and 8 kg are moving with velocities 2ms−1and3ms−1 away from each other along the same line. The velocity of centre of mass is
View SolutionA thin uniform bar lies on a frictionless horizonta surface and is free to move in any way on th surface. Its mass is 0.16 kg and length √3meters. Two particless, each of mass 0.08 kg, are moving on the same surface and towards the bar in a direction perpendicular to the bar, one with a velocity of 10 m/s, and other with 6m/s as shown in fig. The first particle strikes the bar at point A and the other at point B. Points A and B are at a distane of 0.5m from the centre of the bar. The particles strike the bar at the same instant of time and stick to the bar on collision. Calculate the loss of the kinetic energy of the system in the above collision process.
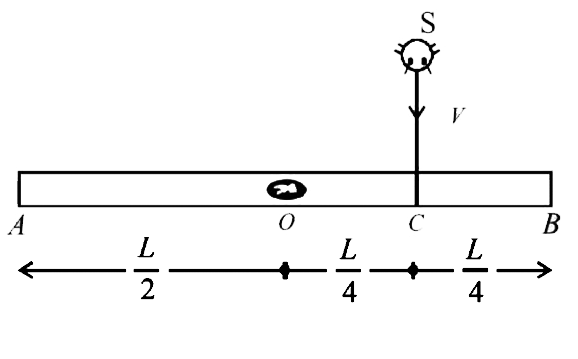
View Solution
