Two identical billiard balls undergo an oblique elastic collision. Initially, one of the balls is stationary. If the initially stationary ball after collision moves in a direction which makes an angle of 37∘ with direction of initial motion of the moving ball, then the angle through which initially moving ball will be deflected is
37∘
60∘
53∘
>53∘
The correct Answer is:C
To solve the problem of the oblique elastic collision between two identical billiard balls, we can follow these steps:
Step 1: Understand the Initial Conditions
- We have two identical billiard balls, A and B.
- Ball A is moving with an initial velocity u towards ball B, which is initially stationary (velocity = 0).
Step 2: Analyze the Collision
- After the collision, ball B moves at an angle of 37∘ with respect to the initial direction of ball A.
- We need to determine the angle through which ball A is deflected after the collision.
Step 3: Apply Conservation of Momentum
- Since the collision is elastic and the balls are identical, we can apply the conservation of momentum in both the x and y directions.
- Let θ be the angle through which ball A is deflected.
Step 4: Set Up the Momentum Equations
1. In the x-direction:
m⋅u=m⋅VB⋅cos(37∘)+m⋅VA⋅cos(θ)
where VB is the velocity of ball B after the collision, and VA is the velocity of ball A after the collision.
2. In the y-direction:
0=m⋅VB⋅sin(37∘)−m⋅VA⋅sin(θ)
Step 5: Simplify the Equations
- Since the masses are identical, we can cancel m from all terms:
1. X-direction:
u=VB⋅cos(37∘)+VA⋅cos(θ)
2. Y-direction:
0=VB⋅sin(37∘)−VA⋅sin(θ)
Step 6: Solve for the Angles
- From the y-direction equation, we can express VA in terms of VB:
VA⋅sin(θ)=VB⋅sin(37∘)⟹VA=VB⋅sin(37∘)sin(θ)
Step 7: Substitute into the X-direction Equation
- Substitute VA into the x-direction equation:
u=VB⋅cos(37∘)+(VB⋅sin(37∘)sin(θ))⋅cos(θ)
Step 8: Factor Out VB
- Factor VB from the equation:
u=VB(cos(37∘)+sin(37∘)⋅cos(θ)sin(θ))
Step 9: Analyze the Geometry
- Since the collision is elastic and involves identical balls, the angle θ can be determined using the geometry of the situation. The angles formed must satisfy the relationship:
θ+37∘+90∘=180∘
Therefore, θ=53∘.
Final Answer
The angle through which the initially moving ball (ball A) will be deflected is 53∘.
---
- We have two identical billiard balls, A and B.
- Ball A is moving with an initial velocity u towards ball B, which is initially stationary (velocity = 0).
- After the collision, ball B moves at an angle of 37∘ with respect to the initial direction of ball A.
- We need to determine the angle through which ball A is deflected after the collision.
- Since the collision is elastic and the balls are identical, we can apply the conservation of momentum in both the x and y directions.
- Let θ be the angle through which ball A is deflected.
1. In the x-direction:
m⋅u=m⋅VB⋅cos(37∘)+m⋅VA⋅cos(θ)
where VB is the velocity of ball B after the collision, and VA is the velocity of ball A after the collision.
0=m⋅VB⋅sin(37∘)−m⋅VA⋅sin(θ)
- Since the masses are identical, we can cancel m from all terms:
1. X-direction:
u=VB⋅cos(37∘)+VA⋅cos(θ)
0=VB⋅sin(37∘)−VA⋅sin(θ)
- From the y-direction equation, we can express VA in terms of VB:
VA⋅sin(θ)=VB⋅sin(37∘)⟹VA=VB⋅sin(37∘)sin(θ)
- Substitute VA into the x-direction equation:
u=VB⋅cos(37∘)+(VB⋅sin(37∘)sin(θ))⋅cos(θ)
- Factor VB from the equation:
u=VB(cos(37∘)+sin(37∘)⋅cos(θ)sin(θ))
- Since the collision is elastic and involves identical balls, the angle θ can be determined using the geometry of the situation. The angles formed must satisfy the relationship:
θ+37∘+90∘=180∘
Therefore, θ=53∘.
The angle through which the initially moving ball (ball A) will be deflected is 53∘.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
Consider an oblique elastic collision between a moving ball and a stationary ball of the same mass. Both the balls move with the same speed after the collision. After the collision, the angle between the directions of motion of two balls is x degree. Find the value of x.
View SolutionA ball moving with a speed of 9ms−1 strikes an identical stationary ball such that after the collision the direction of each ball makes an angle of 30∘ with the original line of motion. The speeds of two balls after the collision is
View Solution
Knowledge Check
A ball , moving with a speed of 10√3m/s , strikes an identical stationary ball such that after the collision , the direction of each ball makes an angle of 30∘with the original line of motion. The speeds of two balla after the collision are , respectively.
A3ms−1,3ms−1B3√3ms−1,3√3ms−1C3√3ms−1,3ms−1D3ms−1,3√3ms−1
A billiard ball moving at a speed of 6.6 ms–1 strikes an identical stationary ball a glancingblow. After the collision, one ball is found to be moving at a speed of 3.3, ms–1 in a direction making an angle of 60º with the original line of motion. The velocity of the other ball is
View SolutionA ball of mass 1 kg moving with a velocity of 0.4 ms−1 collides with another stationary ball. After the collision, the first ball moves with a velocity of 0.3ms1 in a direction making an angle of 90∘ with its initial direction. The momentum of the second ball after the collision will be (in kg ms−1)
View SolutionA ball A of mass M collides elastically with a similar ball B at rest as shown in figure. Initially velocity of ball A is u m/s. After collision,

View SolutionA ball moving along a straight line collides elastically with another stationary ball of the same mass. At the moment of collision, the angle between the straight line passing through the centres of the balls and the direction of tr initial motion of the striking ball is θ, find the fraction of the kinetic energy of the striking ball converted into potential energy at the moment of the maximum deformation.
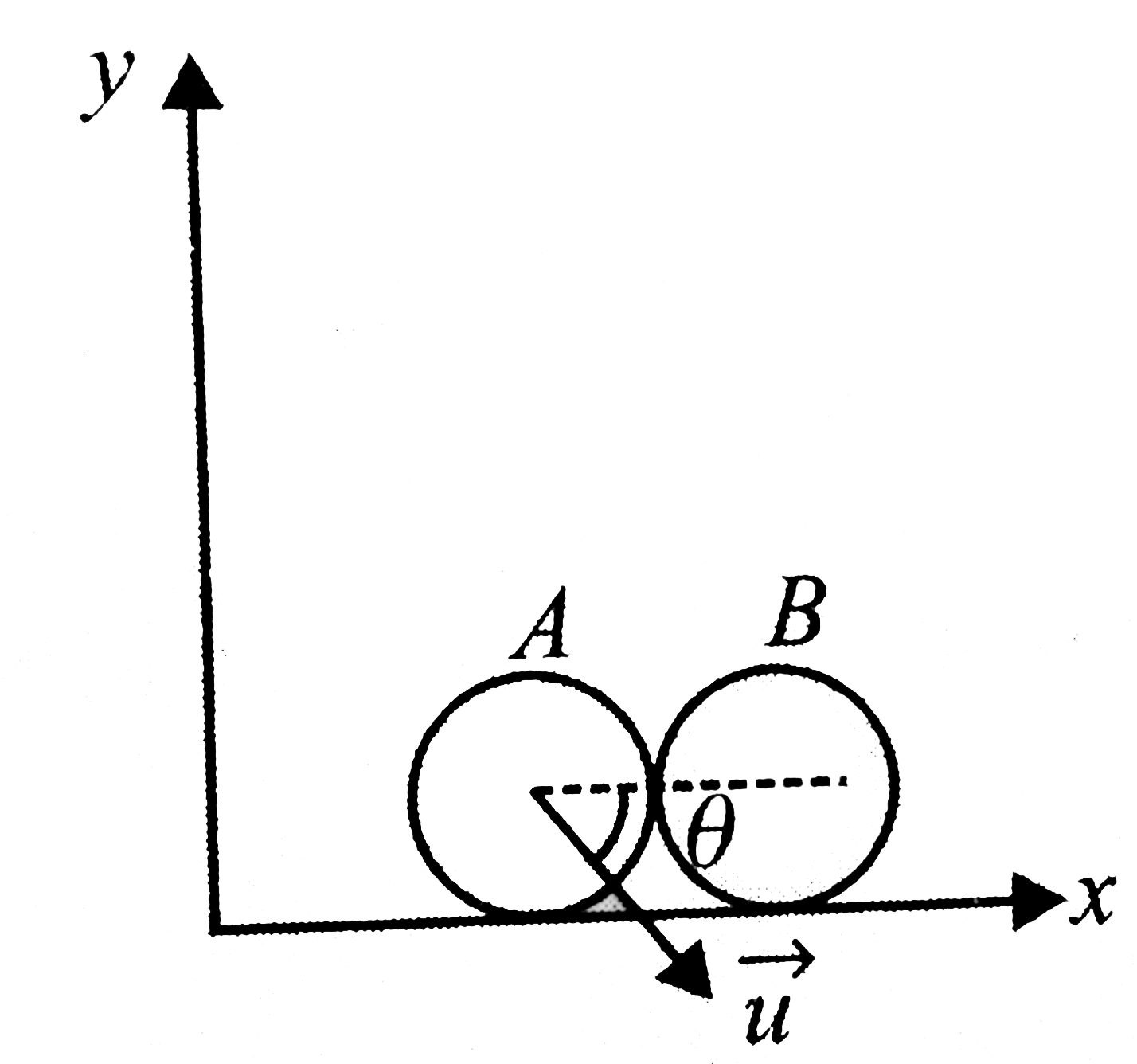
View SolutionA ball of mass 4 kg moving on a smooth horizontal surface makes an elastic collision with another ball of mass m at rest in the line of motion of first ball. If after collision first ball moves in the same direction with one fourth of its velocity before collision, then mass of second ball is
View SolutionTwo balls of equal masses m each undergo oblique collision. If colision is perfectly elastic, then angle between their velocities after collision is
View SolutionTwo billiard balls undergo a head-on collision. Ball 1 is twice as heavy as ball 2. Initially, ball 1 moves with a speed v towards ball 2 which is at rest. Immediately after the collision, ball 1 travels at a speed of v/3 in the same direction. What type of collision has occured?
View Solution
