Two identical blocks A and B each of mass 2kg are hanging stationary by a light inextensible flexible string, passing over a light and frictionless pulley, as shown in Fig. A shell C of mass 1kg moving vertically upwards with velocity 9m/s collides with block B and gets stuck to it.

The loss of mechanical energy up to that instant is
32.4J
40J
16.5J
12.5J
The correct Answer is:A
When C strikes with B, the combined body starts to rise vertically upward. According to law of conservation of momentum, velocity v0 of combined body (just after collision) is given by
(2+1)v0=1×9 or v0=3m/s
But A is at rest. Therefore, string becomes slack and bodies move under gravity, combined body upwards and A downwards till string again becomes taut. This happens when downward displacement of A becomes equal to upward displacement of combined body. Let it happen at instant t1. Then,
12gt21=3t1−12gt21
or t1=0.3s Displacement of each block at that instant,
h1=12gt210.45m
And velocity of combined body is 3−gt1=0 and velocity of A is gt1=3m/s (downward).
Since at this instant, velocities are different, therefore an impulse is developed in the string and magnitude of velocities of bodies becomes equal. Let that velocity magnitude be v and impulse developed be J. This impulse acts upwards on both the bodies.
Hence for A
2×3−J=v’………i
and for combined body,
J=3v’…………..ii
From above equations
v’=1.2m/s
Now combined body starts to move upwards with velocity v’=1.2m/s and retardation a, where
a=3−23+2=2m/s2
Combined body comes to an instantaneous rest after time
t2=v′a=0.6s
After this instant, combined body starts moving down. Time interval between this instant and instant of collision is given by
t1+t2=0.3+0.6=0.9s
Further height ascended by combined body during time t2 is
h2=v’v2−12at22=0.36m
Maximum height raised by combined body is
h=h1+h2=0.81m
Loss of energy during collision of B and C is
E1=12×1×92−123v20=27J
Loss of energy when impulse is developed in string is
E2=12×2x32−12(2+3)3v20(2+3)(v’)2=5.4J
Loss of mechanical energy till B reaches highest point is
E=E1+E2=27+5.4=32.4J
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Integer
16 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
Two identical blocks A and B each of mass 2 kg hanging stationsary by a light inextensible flexible string passing over a light and frictionless pulley. A shot C, of mass 1 kg moving vertically with velocity 9 m/s collides with block B and get stuck to it. Calculate :
Time after which block B starts moving downward
Maximum height reached by B
Loss of mechanical energy upto that instant
View SolutionThree blocks A,B and C of mass 10 kg each are hanging on a string passing over a fixed frictionless pulley as shown in figure. The tension in the string connecting blocks B and C is (g=10m/s2)
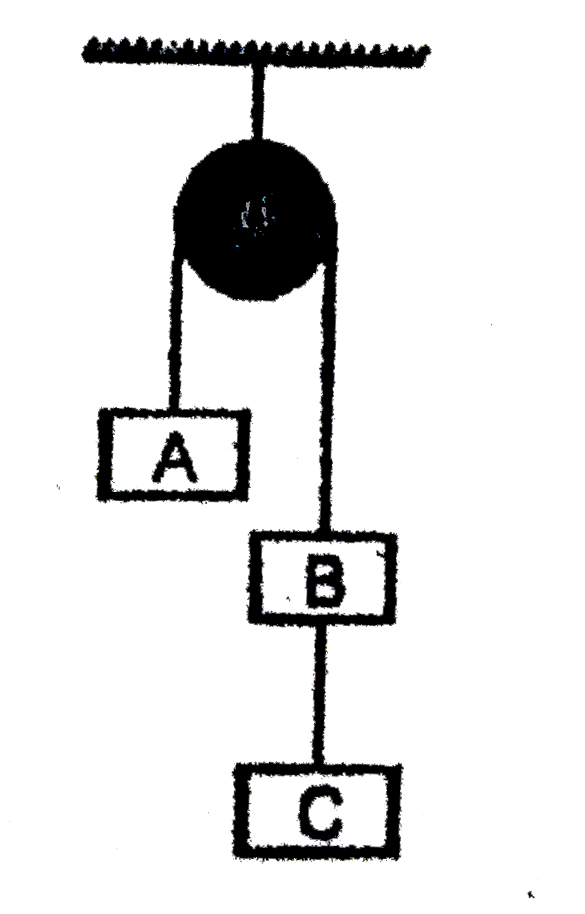
View Solution
Knowledge Check
Two identical blocks A and B each of mass 2kg are hanging stationary by a light inextensible flexible string, passing over a light and frictionless pulley, as shown in Fig. A shell C of mass 1kg moving vertically upwards with velocity 9m/s collides with block B and gets stuck to it.

The maximum height reached by BA0.81mB0.36mC0.49mD0.25mTwo identical blocks A and B each of mass 2kg are hanging stationary by a light inextensible flexible string, passing over a light and frictionless pulley, as shown in Fig. A shell C of mass 1kg moving vertically upwards with velocity 9m/s collides with block B and gets stuck to it.

Calculate the time after which block B starts moving downwards.A0.90sB1sC0.60sD0.30sTwo blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
Two blocks A and B , each of mass 10kg , are connected by a light string passing over a smooth pulley as shown in the figure. Block A will remain at rest if the friction on it is

View SolutionTwo masses 6 kg and 4 kg are connected by massless flexible and inextensible string passing over massless and frictionless pulley.The acceleration of centre of mass is (g=10ms^2)
View SolutionIn the shown ,two blocks one of mass 5kg and the other of mass 2kg are connected by light and inextensible string Pulleys are light an d frictionless Choose the correct statement
 .
.
View SolutionTwo masses M1=5kg,M2=10kg are connected at the ends of an inextensible string passing over a frictionless pulley as shown. When masses are released, then acceleration of masses will be
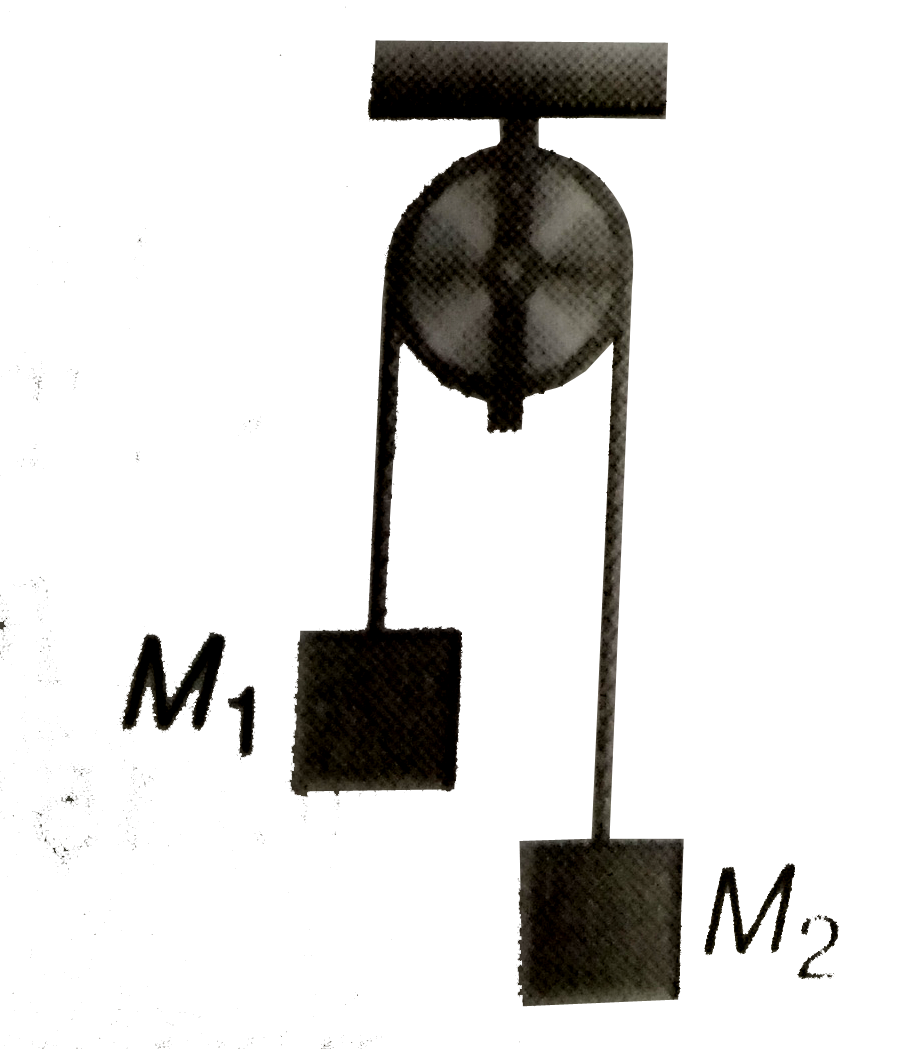
View SolutionThree equal weight A,B and C of mass 2kg each are hanging on a string passing over a fixed frictionless pulley as shown in the figure. The tension in the string connecting weights B and C is approximately

View Solution
