Two identical cells each of emf ε, having negligible internal reistance r, are connercted in parallel with each other across an external resistance R. What is the current through this resistance.
To solve the problem, we need to determine the current flowing through the external resistance R when two identical cells, each with an electromotive force (emf) ϵ and negligible internal resistance r, are connected in parallel.
1. Identify the Configuration:
- We have two identical cells connected in parallel. Each cell has an emf ϵ and negligible internal resistance r.
2. Determine the Equivalent EMF:
- For cells connected in parallel, the equivalent emf Eeq remains the same as the emf of each individual cell. Therefore,
Eeq=ϵ
3. Calculate the Equivalent Internal Resistance:
- Since both cells have negligible internal resistance, we can denote the internal resistance of each cell as r. When connected in parallel, the equivalent internal resistance req can be calculated using the formula for resistors in parallel:
1req=1r+1r=2r⟹req=r2
- However, since r is negligible, req can also be considered negligible.
4. Apply Ohm's Law:
- The total current I flowing through the external resistance R can be calculated using Ohm's law. The total voltage across the external resistance is the equivalent emf Eeq, and the total resistance in the circuit is the sum of the external resistance R and the equivalent internal resistance req:
I=EeqR+req
- Substituting Eeq=ϵ and req≈0 (since it is negligible):
I=ϵR+0=ϵR
5. Final Result:
- Thus, the current through the external resistance R is:
I=ϵR
- We have two identical cells connected in parallel. Each cell has an emf ϵ and negligible internal resistance r.
- For cells connected in parallel, the equivalent emf Eeq remains the same as the emf of each individual cell. Therefore,
Eeq=ϵ
- Since both cells have negligible internal resistance, we can denote the internal resistance of each cell as r. When connected in parallel, the equivalent internal resistance req can be calculated using the formula for resistors in parallel:
1req=1r+1r=2r⟹req=r2
- However, since r is negligible, req can also be considered negligible.
- The total current I flowing through the external resistance R can be calculated using Ohm's law. The total voltage across the external resistance is the equivalent emf Eeq, and the total resistance in the circuit is the sum of the external resistance R and the equivalent internal resistance req:
I=EeqR+req
- Substituting Eeq=ϵ and req≈0 (since it is negligible):
I=ϵR+0=ϵR
- Thus, the current through the external resistance R is:
I=ϵR
Topper's Solved these Questions
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [Set- II]4videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [Set-III]3videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET-III, DELHI BOARD4videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D6videos
SAMPLE PAPER 2019
Similar Questions
Knowledge Check
- Question 1 - Select One
If n cells each of emf E and internal resistance rare connected in parallel, then the total emf and internal resistances will be
Aε,rnBε,nrCnε,rnDnε,nr - Question 2 - Select One
In a circuit a cell with internal resistance r is connected to an external resistance R. The condition for the maximum current that drawn from the cell is
AR=rBR<rCR>rDR=0
n identical cells, each of emf E and internal resistance r, are joined in series to form a closed circuit. Find the potential difference across any one cell.
View SolutionTwo identical batteries each of emf E=2 volt and internal resistance r=1 ohm are available t. produce heat in an external resistance by passing a current through it. What is the maximum power that can be developed across an external resistance R using these batteries?
View SolutionA group of six identical cells each of emf E and internal resistance r are joined in series to form a loop. The terminal voltage across each cells is
View SolutionSeven identical cells each of e.m.f. E and internal resistance r are connected as shown . The potential difference between A and B is
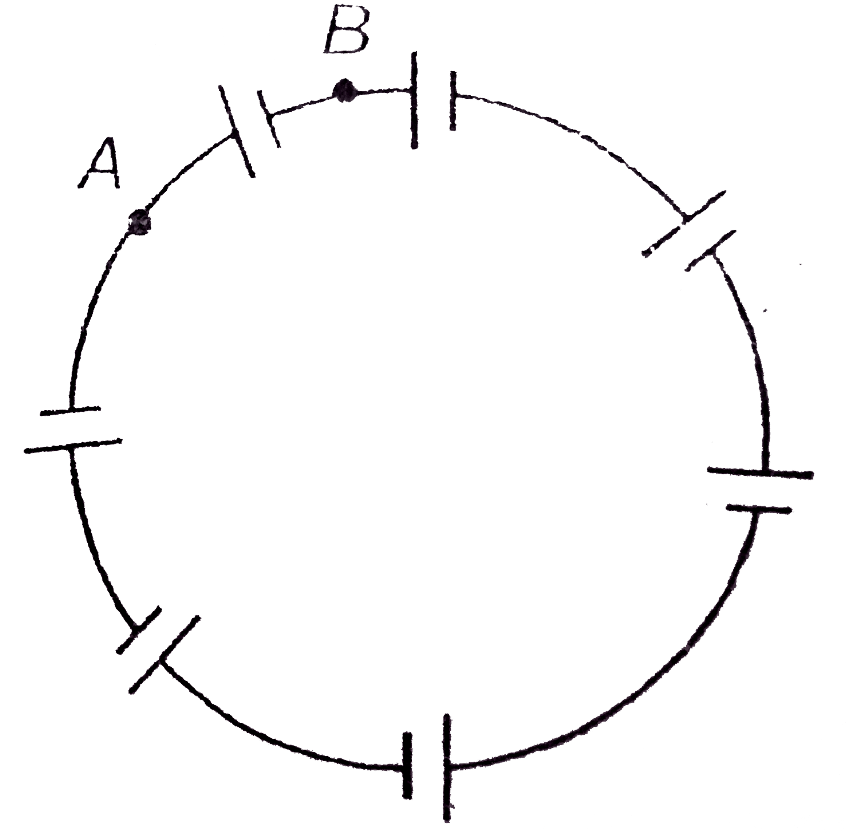 View Solution
View SolutionFour cells, each of emf E and internal resistance r, are connected in series across an external resistance R. By mistake one of the cells is connected in reverse. Then, the current in the external circuit is
View SolutionConsider N=n1n2indentical cells, each of emf(ε) and internal resistance r. Suppose n1 cells are joined in series to forn a line and n_(2) such are connected in parallel. The combination drives a current in an external resistance R.(a) find the current in the external resistance, (b) Assuming that n1and n_(2) can be continuously varied, find the relation between n_(1) ,n_(2) R and r for which the current in R in maximum.
View Solution

