Two identical batteries each of emf E=2 volt and internal resistance r=1 ohm are available t. produce heat in an external resistance by passing a current through it. What is the maximum power that can be developed across an external resistance R using these batteries?
The correct Answer is:B
To find the maximum power that can be developed across an external resistance R using two identical batteries, we will consider both series and parallel configurations of the batteries.
Step 1: Analyze the Series Configuration
1. Connect the batteries in series: When connected in series, the total EMF Etotal is the sum of the individual EMFs, and the total internal resistance rtotal is the sum of the internal resistances.
Etotal=E+E=2+2=4 volts
rtotal=r+r=1+1=2 ohms
Step 2: Calculate the Current in Series
2. Use Ohm's Law to find the current I:
The total resistance in the circuit is R+rtotal:
I=EtotalR+rtotal=4R+2
Step 3: Calculate Power in Series
3. Calculate the power P across the external resistance R:
The power across the external resistance is given by:
P=I2R=(4R+2)2R
To find the maximum power, we set R=rtotal=2 ohms:
Pmax=(42+2)2⋅2=(44)2⋅2=12⋅2=2 watts
Step 4: Analyze the Parallel Configuration
4. Connect the batteries in parallel: When connected in parallel, the EMF remains the same, but the internal resistance is halved:
Eparallel=E=2 volts
rparallel=r2=12 ohm
Step 5: Calculate the Current in Parallel
5. Use Ohm's Law to find the current I:
The total resistance in the circuit is R+rparallel:
I=EparallelR+rparallel=2R+12
Step 6: Calculate Power in Parallel
6. Calculate the power P across the external resistance R:
The power across the external resistance is given by:
P=I2R=⎛⎝2R+12⎞⎠2R
To find the maximum power, we set R=rparallel=12 ohms:
Pmax=⎛⎝212+12⎞⎠2⋅12=(21)2⋅12=4⋅12=2 watts
Conclusion
In both configurations (series and parallel), the maximum power that can be developed across the external resistance R is:
Maximum Power=2 watts
1. Connect the batteries in series: When connected in series, the total EMF Etotal is the sum of the individual EMFs, and the total internal resistance rtotal is the sum of the internal resistances.
Etotal=E+E=2+2=4 volts
rtotal=r+r=1+1=2 ohms
2. Use Ohm's Law to find the current I:
The total resistance in the circuit is R+rtotal:
I=EtotalR+rtotal=4R+2
3. Calculate the power P across the external resistance R:
The power across the external resistance is given by:
P=I2R=(4R+2)2R
To find the maximum power, we set R=rtotal=2 ohms:
Pmax=(42+2)2⋅2=(44)2⋅2=12⋅2=2 watts
4. Connect the batteries in parallel: When connected in parallel, the EMF remains the same, but the internal resistance is halved:
Eparallel=E=2 volts
rparallel=r2=12 ohm
5. Use Ohm's Law to find the current I:
The total resistance in the circuit is R+rparallel:
I=EparallelR+rparallel=2R+12
6. Calculate the power P across the external resistance R:
The power across the external resistance is given by:
P=I2R=⎛⎝2R+12⎞⎠2R
To find the maximum power, we set R=rparallel=12 ohms:
Pmax=⎛⎝212+12⎞⎠2⋅12=(21)2⋅12=4⋅12=2 watts
In both configurations (series and parallel), the maximum power that can be developed across the external resistance R is:
Maximum Power=2 watts
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 Single Correct26videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 More Than One Correct10videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - OBJECTIVE_TYPE1videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective11videos
COMMUNICATION SYSTEM
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery25videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Two indentical batteries, each of emf 2V andinternal resistance r=1Ω are connected as shown. The maximum power that can be developed across R using these batteries is
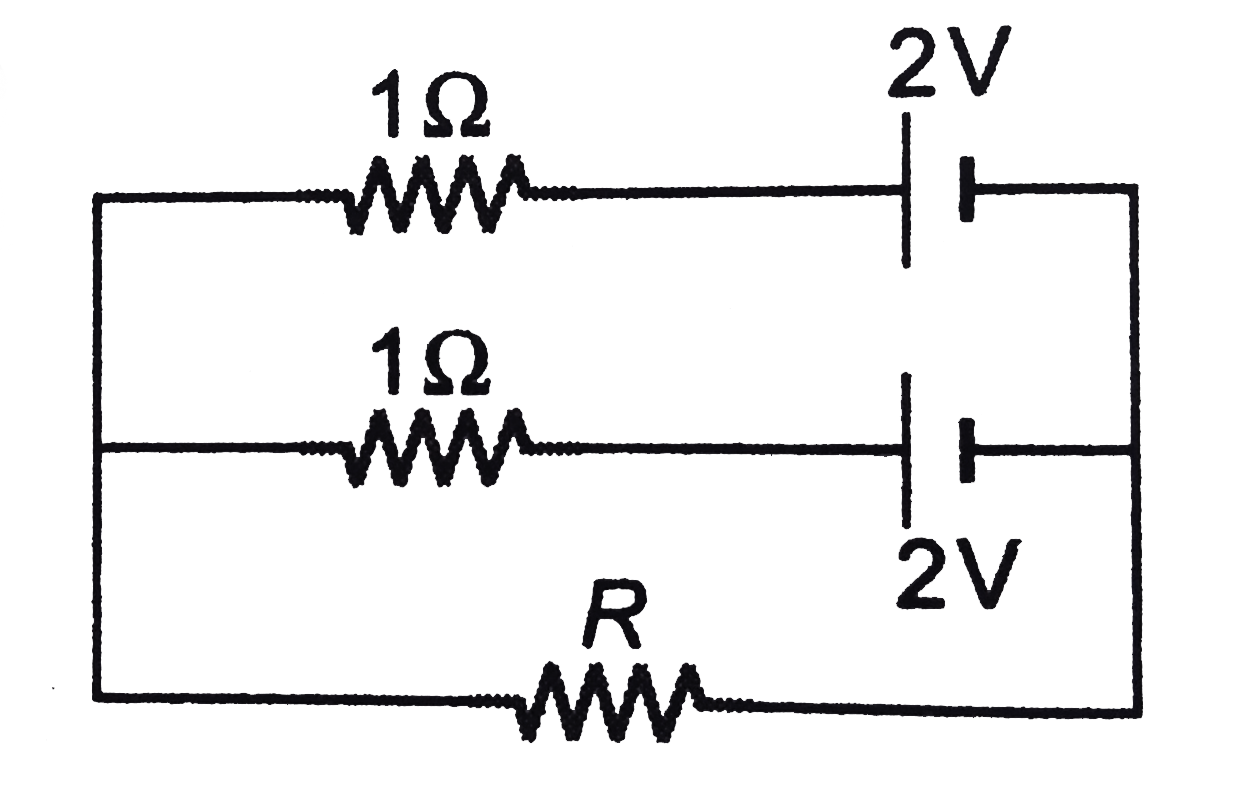 View Solution
View SolutionTwo identical cells each of emf ε, having negligible internal reistance r, are connercted in parallel with each other across an external resistance R. What is the current through this resistance.
View Solutionn identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
View Solution24 cells of emf 1.5V each having internal resistance of 1 ohm are connected to an external resistance of 1.5 ohms. To get maximum current,
View SolutionA battery is of emt E and internal resistance R. The value of external resistance r so that the power across eternal resistance is maximum :
View SolutionA cell of internal resistance r drivers current through an external resistance R. The power delivered by the to the external resistance will be maximum when:
View SolutionFour resistance are connected to a DC battery as shown in figure. Maximum power will be developed across ......... Ohm resistance.
 View Solution
View SolutionThe emf of a battery is 2V and its internal resistance is 0.5Ω the maximum power which it can deliver to any external circuit will be
View SolutionA battery of six cells each of e.m.f . 2V and internal resistance 0.5Ω is being charged by D.C. mains of e.m.f. 220V by using an external resistance of 10Ω. What is the potential difference across the battery?
View SolutionThe figure shows a source (a battery) with an emf E of 12 V with an internal resistance r of 2Ω and an external resistance of 4Ω is added to complete the circuit. What are the voltmeter and ammeter readings
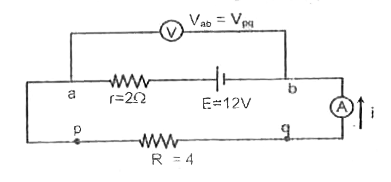 View Solution
View Solution

