Two identical charged spheres of material density ρ, suspended from the same point by inextensible strings of equal length make an angle θ between the string. When suspended in a liquid of density σ the angle θ remains the same. The dielectric constant K of the liquid is
ρρ−σ
ρ−σρ
ρρ+σ
ρ+σρ
The correct Answer is:A
To solve the problem, we need to analyze the forces acting on the charged spheres when they are suspended in air and then in a liquid. Here’s a step-by-step solution:
Step 1: Analyze the forces acting on the spheres in air
When the two identical charged spheres are suspended in air, the forces acting on each sphere are:
- The gravitational force (weight) acting downwards: mg
- The tension in the string acting at an angle θ/2
- The electrostatic repulsive force between the two charged spheres
From the equilibrium of forces, we can write:
1. The vertical component of the tension balances the weight:
Tcos(θ2)=mg
2. The horizontal component of the tension balances the electrostatic force:
Tsin(θ2)=Fe
Where Fe is the electrostatic force given by Coulomb's law:
Fe=kq2r2
Step 2: Relate the forces using tangent
From the above equations, we can derive:
tan(θ2)=Femg=kq2r2mg
Step 3: Analyze the forces acting on the spheres in the liquid
When the spheres are submerged in a liquid of density σ, the forces acting on each sphere are:
- The gravitational force (weight) acting downwards: mg
- The buoyant force acting upwards: Fb=σVg (where V is the volume of the sphere)
- The tension in the string acting at an angle θ/2
The equilibrium of forces gives us:
1. The vertical component of the tension:
Tcos(θ2)=mg−Fb
2. The horizontal component of the tension still balances the electrostatic force:
Tsin(θ2)=F′e
Where F′e is the electrostatic force in the liquid:
F′e=1Kkq2r2
Step 4: Set up the equations for the liquid case
From the equations for the liquid case, we can write:
tan(θ2)=F′emg−Fb
Substituting Fb=σVg (where V=43πr3 for a sphere) gives:
tan(θ2)=1Kkq2r2mg−σVg
Step 5: Equate the two expressions for tangent
Since the angle θ remains the same in both cases, we can equate the two expressions for tan(θ2):
kq2r2mg=1Kkq2r2mg−σVg
Step 6: Simplify and solve for K
Cross-multiplying and simplifying gives:
mg−σVg=mgK1
Rearranging gives:
K=mgmg−σVg
Step 7: Substitute volume of the sphere
Substituting V=43πr3:
K=ρρ−σ
Where ρ is the density of the material of the spheres.
Final Answer
The dielectric constant K of the liquid is:
K=ρρ−σ
When the two identical charged spheres are suspended in air, the forces acting on each sphere are:
- The gravitational force (weight) acting downwards: mg
- The tension in the string acting at an angle θ/2
- The electrostatic repulsive force between the two charged spheres
1. The vertical component of the tension balances the weight:
Tcos(θ2)=mg
2. The horizontal component of the tension balances the electrostatic force:
Tsin(θ2)=Fe
Fe=kq2r2
From the above equations, we can derive:
tan(θ2)=Femg=kq2r2mg
When the spheres are submerged in a liquid of density σ, the forces acting on each sphere are:
- The gravitational force (weight) acting downwards: mg
- The buoyant force acting upwards: Fb=σVg (where V is the volume of the sphere)
- The tension in the string acting at an angle θ/2
1. The vertical component of the tension:
Tcos(θ2)=mg−Fb
2. The horizontal component of the tension still balances the electrostatic force:
Tsin(θ2)=F′e
F′e=1Kkq2r2
From the equations for the liquid case, we can write:
tan(θ2)=F′emg−Fb
Substituting Fb=σVg (where V=43πr3 for a sphere) gives:
tan(θ2)=1Kkq2r2mg−σVg
Since the angle θ remains the same in both cases, we can equate the two expressions for tan(θ2):
kq2r2mg=1Kkq2r2mg−σVg
Cross-multiplying and simplifying gives:
mg−σVg=mgK1
Rearranging gives:
K=mgmg−σVg
Substituting V=43πr3:
K=ρρ−σ
The dielectric constant K of the liquid is:
K=ρρ−σ
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Assertion and Reason
15 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Match the columns
5 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.5
20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
Two identical charged spheres are suspended by strings of equal lengths. The strings make an angle of 30∘ with each other. When suspended in a liquid of density 0.8gcm−3, the angle remains the same. If density of the material of the sphere is 1.6gcm−3, the dielectric constant of the liquid is
View SolutionTwo identical charged spheres are suspended by strings of equal lengths. The strings make an angle of 30∘ with each other. When suspended in a liquid of density 0.8gcm−3, the angle remains the same. If density of the material of the sphere is 1.6gcm−3, the dielectric constant of the liquid is
View SolutionTwo identical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionTwo indentical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionIn a liquid medium of dielectric constant K and of specific gravity 2, two identically charged spheres are suspended from a fixed point by threads of equal lengths. The angle between them is 90∘. In another medium of unknown dielectric constant K1, and specific gravity 4, the angle between them becomes 120∘. If density of material of spheres is 8gm/cc then find K1.
View SolutionTwo identical balls each having a density ρ are suspended from as common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle θ with vertical. Now, both the balls are immersed in a liquid. As a result the angle θ does not change. The density of the liquid is σ. Find the dielectric constant of the liquid.
View SolutionTwo identical balls each having a density ρ are suspended from as common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle θ with vertical. Now, both the balls are immersed in a liquid. As a result the angle θ does not change. The density of the liquid is σ. Find the dielectric constant of the liquid.
View SolutionTwo small spheres each of mass m and charge q are tied from the same rigid support with the help of silk threads of length L. They make angle θ with the vertical as shown in the fig. If length L is decreased, then angle θ with the vertical.
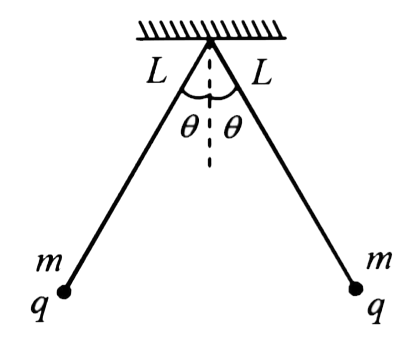
View SolutionTwo positively charged sphere of masses m1 and m2 are suspended from a common point at the ceiling by identical insulating massless strings of length l. Charges on the two spheres are q1 and q2 respectively. Equilibrium both strings make the same angle θ with the vertical. then
View SolutionTwo path balls carrying equal charges are suspended from a common point by strings of equal length, the strings are rightly clamped at half the height. The equilibrium separation between the balls, now becomes :
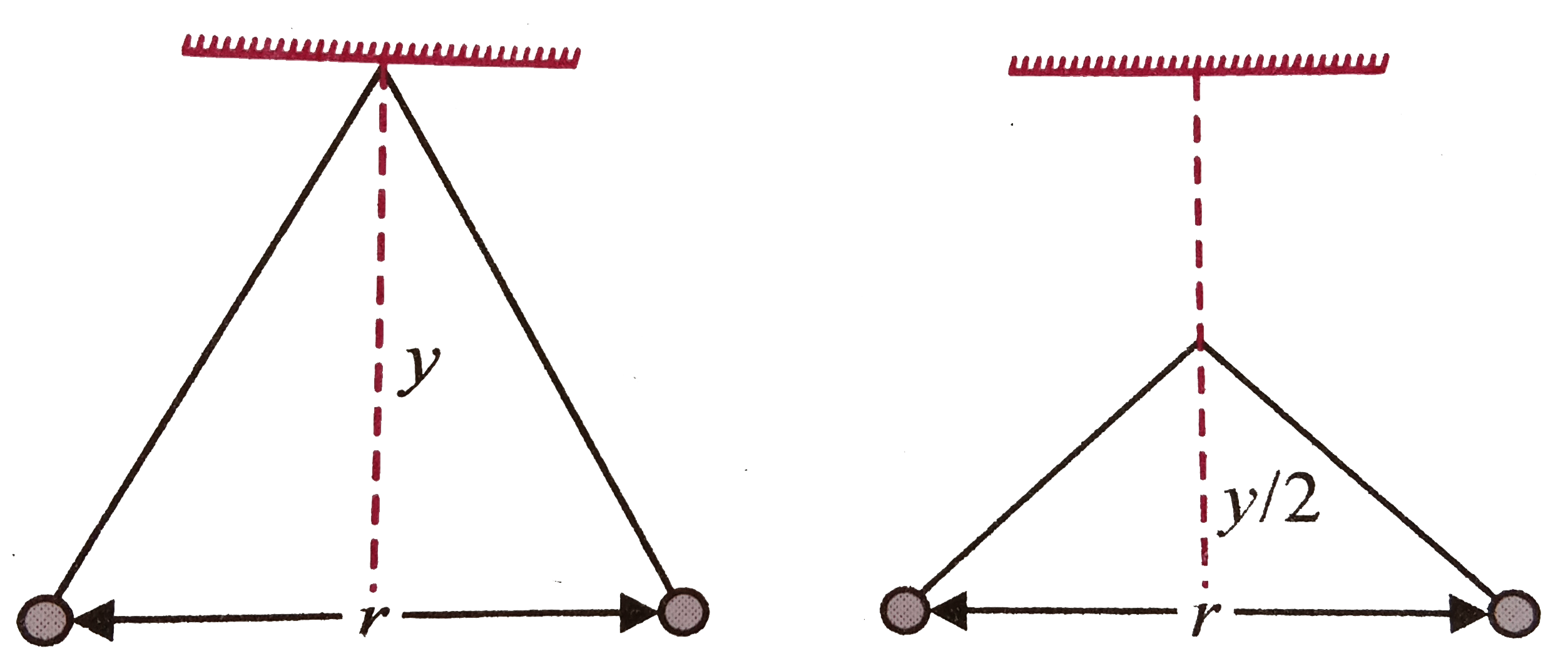
View Solution
