Two identical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
To solve the problem of finding the mass of each pith ball suspended by strings at an angle of 2θ in equilibrium, we can follow these steps:
Step 1: Understand the Setup
We have two identical pith balls, each carrying a charge q, suspended by strings of equal length l. The angle between the strings is 2θ, which means each string makes an angle θ with the vertical.
Step 2: Identify Forces Acting on the Balls
In equilibrium, each ball experiences:
- The gravitational force acting downward: mg
- The tension T in the string acting along the string
- The electrostatic force of repulsion FE between the two charged balls
Step 3: Determine the Geometry
The horizontal distance R between the two balls can be expressed in terms of the length of the string l and the angle θ:
R=2Lsin(θ)
Step 4: Write the Equations for Forces
For each ball, we can write two equations based on the forces acting on it:
1. The vertical component of the tension balances the weight:
Tcos(θ)=mg(Equation 1)
2. The horizontal component of the tension equals the electrostatic force:
Tsin(θ)=FE=kq2R2(Equation 2)
Step 5: Substitute R in the Electrostatic Force Equation
Substituting R=2Lsin(θ) into the electrostatic force equation:
FE=kq2(2Lsin(θ))2=kq24L2sin2(θ)
Step 6: Divide the Two Equations
Dividing Equation 2 by Equation 1 to eliminate T:
Tsin(θ)Tcos(θ)=kq24L2sin2(θ)mg
This simplifies to:
tan(θ)=kq24L2mgsin2(θ)
Step 7: Solve for Mass m
Rearranging the equation gives:
m=kq24L2gsin2(θ)tan(θ)
Final Expression for Mass
Thus, the mass m of each pith ball is given by:
m=kq24L2gsin2(θ)tan(θ)
We have two identical pith balls, each carrying a charge q, suspended by strings of equal length l. The angle between the strings is 2θ, which means each string makes an angle θ with the vertical.
In equilibrium, each ball experiences:
- The gravitational force acting downward: mg
- The tension T in the string acting along the string
- The electrostatic force of repulsion FE between the two charged balls
The horizontal distance R between the two balls can be expressed in terms of the length of the string l and the angle θ:
R=2Lsin(θ)
For each ball, we can write two equations based on the forces acting on it:
1. The vertical component of the tension balances the weight:
Tcos(θ)=mg(Equation 1)
2. The horizontal component of the tension equals the electrostatic force:
Tsin(θ)=FE=kq2R2(Equation 2)
Substituting R=2Lsin(θ) into the electrostatic force equation:
FE=kq2(2Lsin(θ))2=kq24L2sin2(θ)
Dividing Equation 2 by Equation 1 to eliminate T:
Tsin(θ)Tcos(θ)=kq24L2sin2(θ)mg
This simplifies to:
tan(θ)=kq24L2mgsin2(θ)
Rearranging the equation gives:
m=kq24L2gsin2(θ)tan(θ)
Thus, the mass m of each pith ball is given by:
m=kq24L2gsin2(θ)tan(θ)
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - question for short answer
14 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 1
9 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - worked out Examples
19 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
Similar Questions
Two indentical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionAssertion : Two identical balls are charged by q. They are suspended from a common point by two insulating threads l each. In equilibrium, the angle between the tension in the threads is 180∘. (Ignore gravity).
Reason : In equilibrium tension in the spring is
T=14πε0q.ql2
View SolutionTwo identical balls each having a density ρ are suspended from as common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle θ with vertical. Now, both the balls are immersed in a liquid. As a result the angle θ does not change. The density of the liquid is σ. Find the dielectric constant of the liquid.
View SolutionTwo identical balls each having a density ρ are suspended from as common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle θ with vertical. Now, both the balls are immersed in a liquid. As a result the angle θ does not change. The density of the liquid is σ. Find the dielectric constant of the liquid.
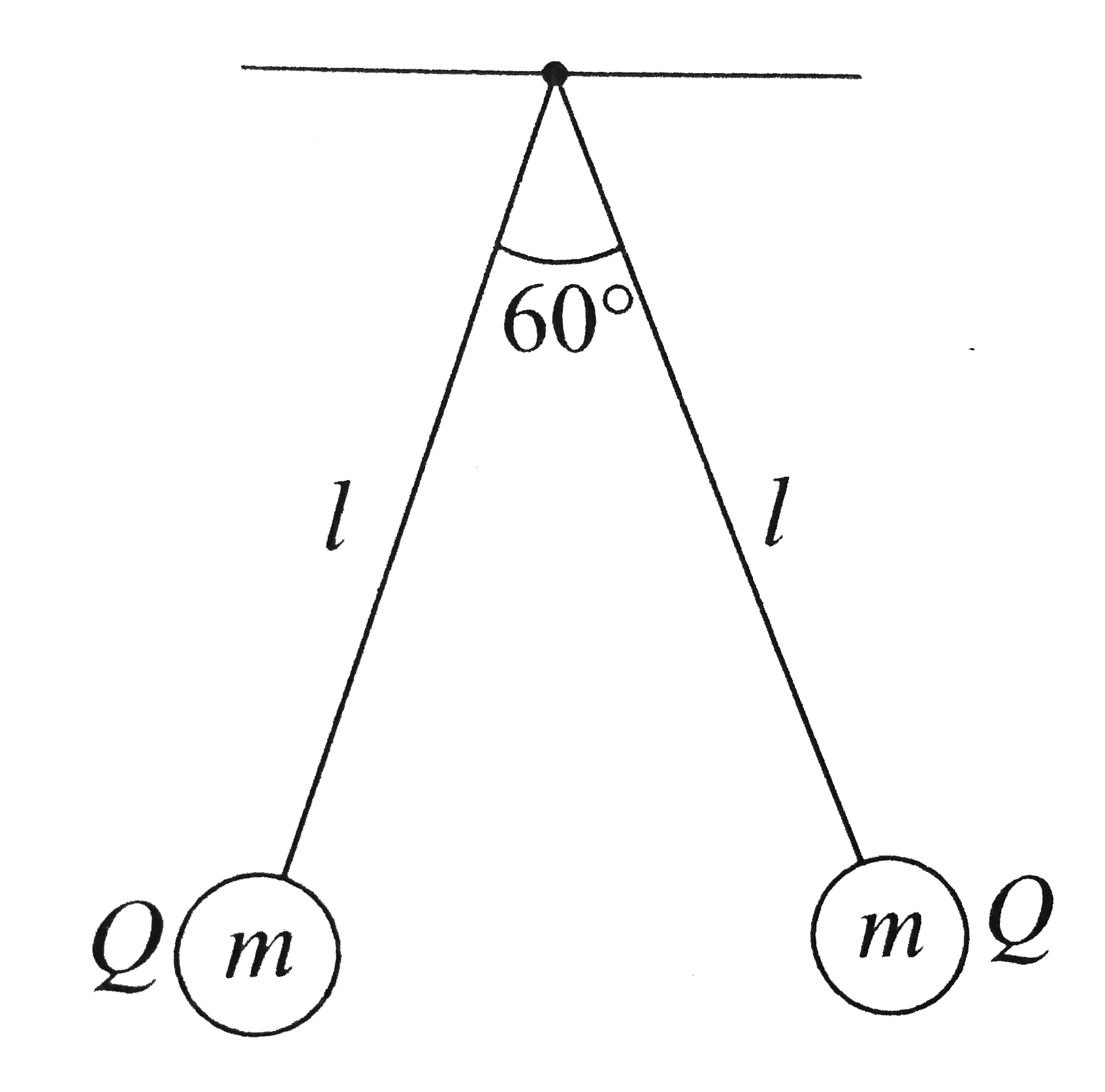
View SolutionTwo small balls, each having equal positive charge Q are suspended by two insulationg strings of equal length l from a hook fixed to a stand. It mass of each ball =m and total angle between the two strings is 60∘m, then find the charge on each ball.
View SolutionTwo identical balls , each having a charge q and mass m , are suspended from a common point by two insultating strings each of length L. The balls are held at a separation x and then released. Find
(a) the electric force on each ball
(b) the component of the resultant force on a ball along and perpendicular to string
(c ) the tension in the string
(d) the acceleration of one of the balls. Consider the situation only for the instant just after the release.
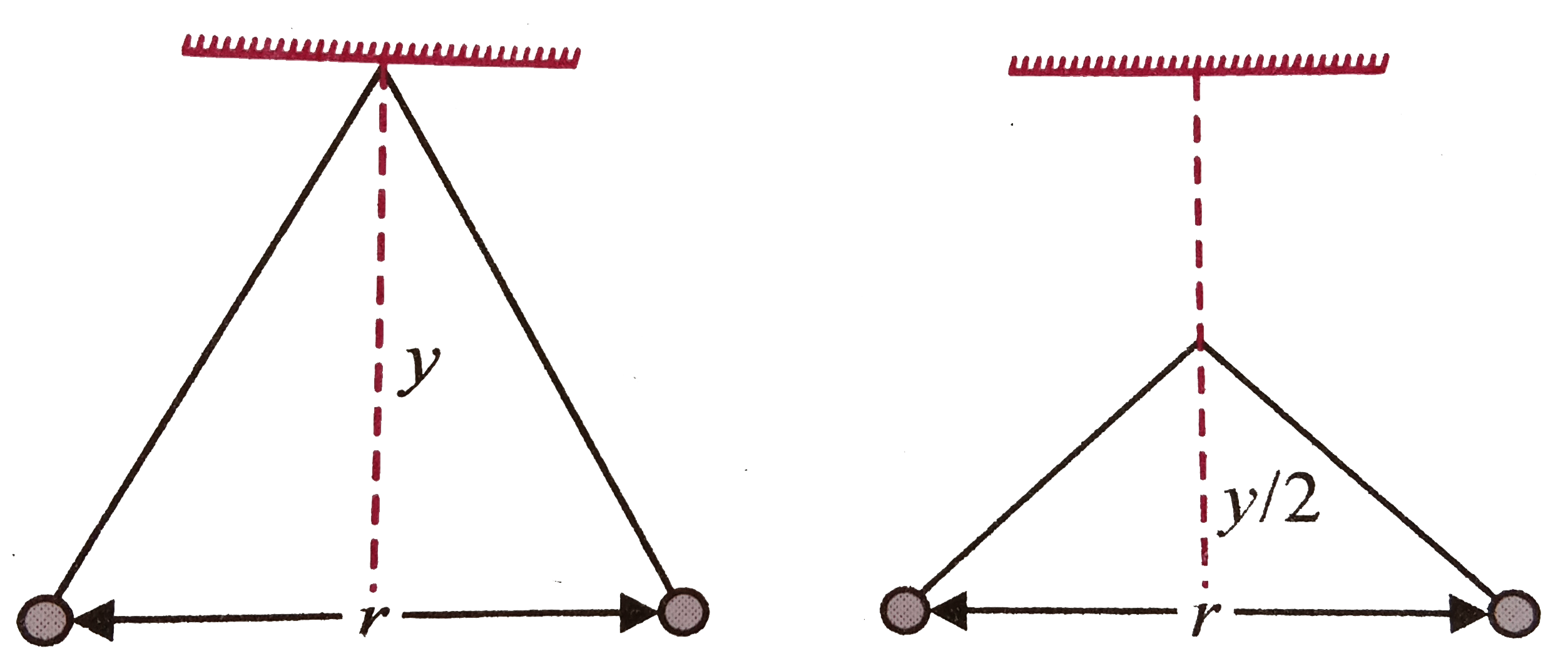
View SolutionTwo pitch balls carrying equal charges are suspended from a common point by strings of equal length, the equilibrium separation between them is r. Now the strings are rigidly clamped at half the height. The equilibrium separation between the balls now become

View SolutionTwo path balls carrying equal charges are suspended from a common point by strings of equal length, the strings are rightly clamped at half the height. The equilibrium separation between the balls, now becomes :
View SolutionTwo identical pith balls are charged by rubbing against each other. They are suspended from a horizontal rod through two strings of length 20 cm each, the separation between the suspension points being 5 cm. in equilibrium, the separation between the balls in 3 cm. Find the mass of each ball and the tension in the strings. the charge on each ball of a magnitude 2.0×10−8C.
View SolutionTwo small spheres, each having a mass of 20 g, are suspended form a common point by two insulating strings of length 40 cm each. The spheres are identically charged and the speration between the balls at equilibrium is found to be 4 cm . Find the charge on each sphere.
View Solution
