Two inductances L1 & L2 are connected in series & are seperated by a large distance.
(a) Show that their equivalent inductance is L1+L2.
(b) Why must their seperation be larger ?
(b) Leq=∑LjLeq−Lj, sum from j = 1 to j = N
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
45 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)
13 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHECKPOINTS
9 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
- ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT EXERCISE - Practice Questions (Integer)
7 Videos
Similar Questions
Inductors in parallel. Two inductors L1 and L2 are connected in parallel and separated by a large distance so that the magnetic field of one cannot affect the other. (a) Show that the equivalent inductance is given by
1Leq=1L1=1L2
(Hint: Review the derivations for resistors in parallel and capacitors in parallel. Which is similar here?) (b) What is the generalization of (a) for N inductors in parallel?
View SolutionTwo coils connected as shown in Fig. 30-48 separately have inductances L1 and L2. Their mutual inductance is M. (a) Show that this combination can be replaced by a single coil of equivalent inductance given by
Leq=L1+L2+2M
(b) How could the coils in Fig. 30-48 be reconnected to yield an equivalent inductance of
Leq=L1+L2−2M?
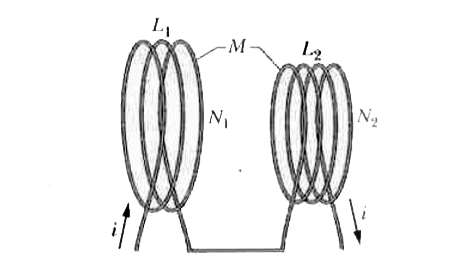
View Solution
Knowledge Check
The inductors of self inductance L1 and L2 are put in series .
AL1+L2onlyBL1−L2onlyCMay be in between L1−L2 and L1+L2DL1+2L2Two inductors L1 and L2 are connected in parallel and a time varying current flows as shown.
the ratio of current i1/i2
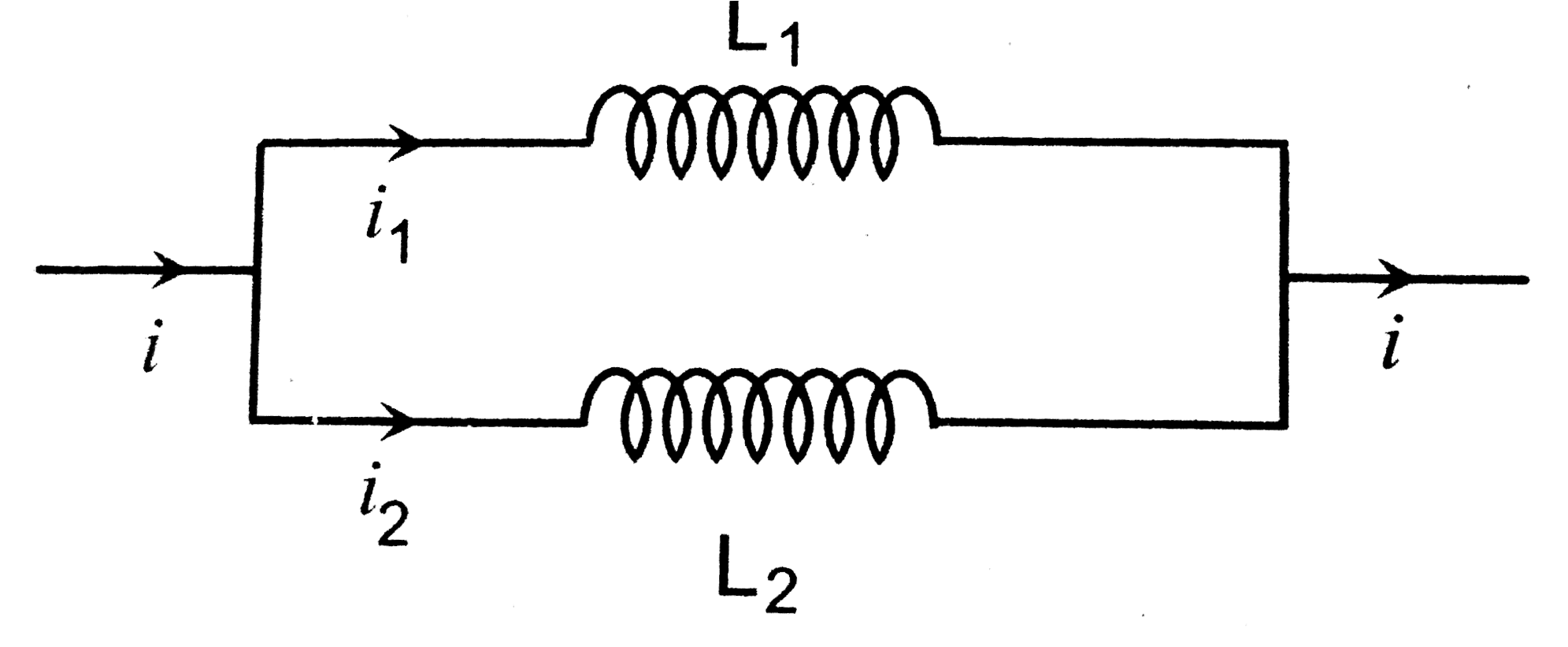 AL1/L2BL2/L1CL21(L1+L22)DL22(L1+L22)
AL1/L2BL2/L1CL21(L1+L22)DL22(L1+L22)Mutual inductance of two coils depends on their self inductance L1 and L2 as :
AM12=L1/L2BM12=L2/L1CM12=√L1L2DM12=√L1/L2
" Two inductors each of inductance L are joined in parallel.Their equivalent inductance is "
View SolutionTwo inductors of inductance L each are connected in series with opposite magnetic fluxes. The resultant inductance is
(Ignore mutual inductance)
View SolutionTwo inductors each of inductance L are joined in parallel. Their equivalent inductance is
View SolutionTwo pure inductors each of self inductance L are connected in series, the net inductance is
View SolutionConsider the line L 1 : x 1 y 2 z 1 312 +++ ==, L2 : x2y2z3 123
View Solution
