Two long and parallel straight wires A and B carrying currents of 8⋅0A and 5⋅0A in the same direction are separated by a distance of 4⋅0cm. Estimate the force on a 10cm section of wire A.
To solve the problem of estimating the force on a 10 cm section of wire A, we will use the formula for the magnetic force between two parallel currents. Here are the steps:
1. Identify the Given Values:
- Current in wire A, I1=8A
- Current in wire B, I2=5A
- Distance between the wires, r=4.0cm=0.04m
- Length of the section of wire A, L=10cm=0.1m
2. Use the Formula for the Force:
The force F exerted on a length L of wire A due to the magnetic field created by wire B is given by the formula:
F=μ0I1I2L2πr
where μ0 (the permeability of free space) is approximately 4π×10−7T m/A.
3. Substitute the Values into the Formula:
F=(4π×10−7)⋅(8)⋅(5)⋅(0.1)2π⋅(0.04)
4. Simplify the Equation:
- The π terms cancel out:
F=(4×10−7)⋅(8)⋅(5)⋅(0.1)2⋅(0.04)
- Calculate the denominator:
2⋅0.04=0.08
- Now the equation becomes:
F=(4×10−7)⋅(8)⋅(5)⋅(0.1)0.08
5. Calculate the Numerator:
4×8×5×0.1=16
- Therefore:
F=16×10−70.08
6. Final Calculation:
- Now divide 16×10−7 by 0.08:
F=16×10−7÷0.08=2×10−5N
Final Answer:
The force on a 10 cm section of wire A is F=2×10−5N.
- Current in wire A, I1=8A
- Current in wire B, I2=5A
- Distance between the wires, r=4.0cm=0.04m
- Length of the section of wire A, L=10cm=0.1m
The force F exerted on a length L of wire A due to the magnetic field created by wire B is given by the formula:
F=μ0I1I2L2πr
where μ0 (the permeability of free space) is approximately 4π×10−7T m/A.
F=(4π×10−7)⋅(8)⋅(5)⋅(0.1)2π⋅(0.04)
- The π terms cancel out:
F=(4×10−7)⋅(8)⋅(5)⋅(0.1)2⋅(0.04)
- Calculate the denominator:
2⋅0.04=0.08
- Now the equation becomes:
F=(4×10−7)⋅(8)⋅(5)⋅(0.1)0.08
4×8×5×0.1=16
- Therefore:
F=16×10−70.08
- Now divide 16×10−7 by 0.08:
F=16×10−7÷0.08=2×10−5N
The force on a 10 cm section of wire A is F=2×10−5N.
Topper's Solved these Questions
Similar Questions
Two parallel wires are carrying electric currents of equal magnitude and in the same direction. They
View SolutionTwo parallel wires carry equal currents of 10A along the same direction and are separated by a distance of 2.0 cm. Find the magnetic field at a point which is 2.0 cm away from each of these wires.
View Solution
Knowledge Check
Two long and parallel straight wires A and B are carrying currents of 4A and 7A in the same directions are separated by a distance of 5cm. The force acting on a 8cm section of wire A is
A3×10−6NB6×10−6NC9×10−6ND12×10−6NTwo straight wires A and B of lengths 10 m and 12 m carrying currents of 4.0 A and 6.0 A respectively in opposite direction, lie parallel to each other at a distance of 3.0 cm. The force on a 15 cm section of the wire B near its centre is
A2.4×10−5N,attractiveB2.4×10−5N,repulsiveC1.2×10−5N,attractiveD1.2×10−5N,attractiveA short conducting rod P of length 3.0cm is placed parallel to an near the centre of a long conducting rod Q of length 3.0 m. Conductors P and carry currents of 3.0 A and 4.0 A respectively in the same direction. The two conductors are separated by a distance of 2.0cm in air. What is the force experienced by the long conductor Q ?
A1.6×10−6NB2.6×10−6NC3.6×10−6ND4.6×10−6N
Two long parallel copper wires carry current of 5A each in opposite directions. If the wires are separated by a distance distance of 0.5m, then the force per unit length between the two wires is
View SolutionTwo long straight wires, each carrying a current I in opposite directions are separated by a distance R. The magnetic induction at a point mid way between the wire is
View SolutionTwo thin, long, parallel wires, separated by a distance 'd' carry a current of 'i' A in the same direction. They will
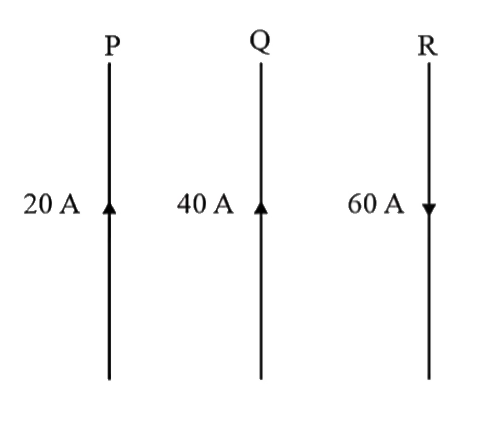
View SolutionP, Q and R are long straight wires in air, carrying currents as shown. The force on Q is directed
View SolutionTwo long parallel wires are 30 cm apart carrying currents 10 A and 15 A respectively in the same direction. The force acting over a length of 5 m of the wires is
View Solution
