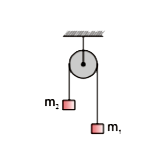
Two mass are attached to a flexible inextensible massless rope, which passes over a frictionless and massless pully. Find the accelerations of the masses and tension in the rope.

Fix an inertial frame to the ground to observe the motion of the masses.
Let the tension in the rope be T(in fact, tension is the property of a point of the rope). In this case with ideal pulley (massless and frictionless) and ideal rope(inextensible,massless, and flexible), the tension will remain constant throughout the rope. Let the acceleration of be vertically downwards, and accelerations on also be a, vertically upwards. This is because the rope is inextensible, during motion, the length of the rope must not change, and the rope must not slacken either.
From the above statement, you must not conclude that the accelerations of the masses connected by a rope are always equal. The relationshop between the accelerations of the masses depends on the configuration of the pulley-rope system , which can be obtained from the fact that the length of an ideal rope must not change and the rope must not slacken.
Using eq. for the force diagram of
...(i)
...(ii)
Adding (i) and (ii) ,
substituting this value of a in (i) we get
...(iv).

Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.1
11 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
Two masses M and m are connected at the two ends of an inextensible string. The string passes over a smooth frictionless pulley. Calculate the acceleration of the masses and the tension in the string. Given M>m.
View SolutionTwo blocks of masses m1 and m2 are attached at the ends of an inextensible string which passes over a smooth massless pulley. If m1>m2, find :
(i) the acceleration of each block
(ii) the tension in the string.
View Solution
Knowledge Check
Two masses m and m (m>m) are connected by massless flexible and inextensible string passed over massless and frictionless pulley. The acceleration of centre of mass is
A(m1−m2m1+m2)2gBm1−m2m1+m2gCm1+m2m1−m2gDZeroTwo masses m1 and m2 are attached to a string which passes over a frictionless smooth pulley. When m1=10kg,m2=6kg, the acceleration of masses is
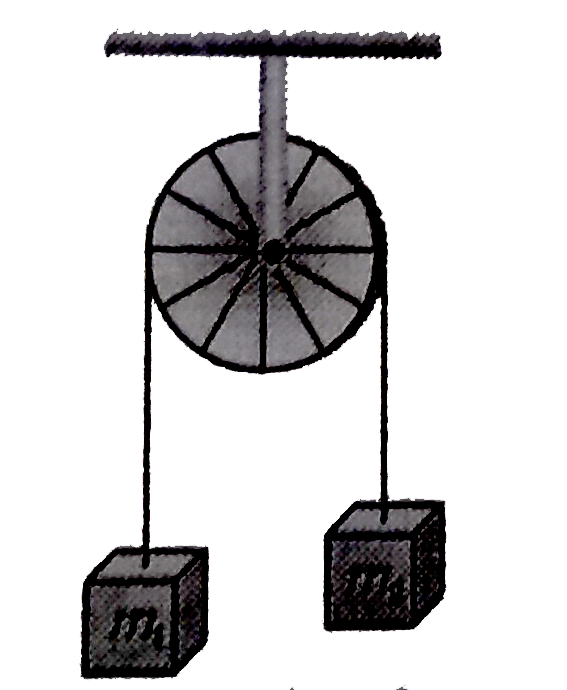 A20m/s2B5m/s2C2.5m/s2D10m/s2
A20m/s2B5m/s2C2.5m/s2D10m/s2Two bodies of masses m1 and m2 are connected a light string which passes over a frictionless massless pulley. If the pulley is moving upward with uniform acceleration g2, then tension in the string will be
A3m1m2m1+m2gBm1+m24m1m2gC2m1m2m1+m2gDm1m2m1+m2g
Two masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
View SolutionTwo bodies of massless string passing over a frictionless pulley. The acceleration of the system is (g=9.8m/s2)
View SolutionTwo mass m and 2m are attached with each other by a rope passing over a frictionless and massless pulley. If the pulley is accelerated upwards with an acceleration 'a', what is the value of tension?
View SolutionTwo masses m1 and m2 are attached to the ends of a massless string which passes over a frictionless pulley attached to the top of an inclined plane. The angle of inclination of the plane is θ. Take g=10ms−2
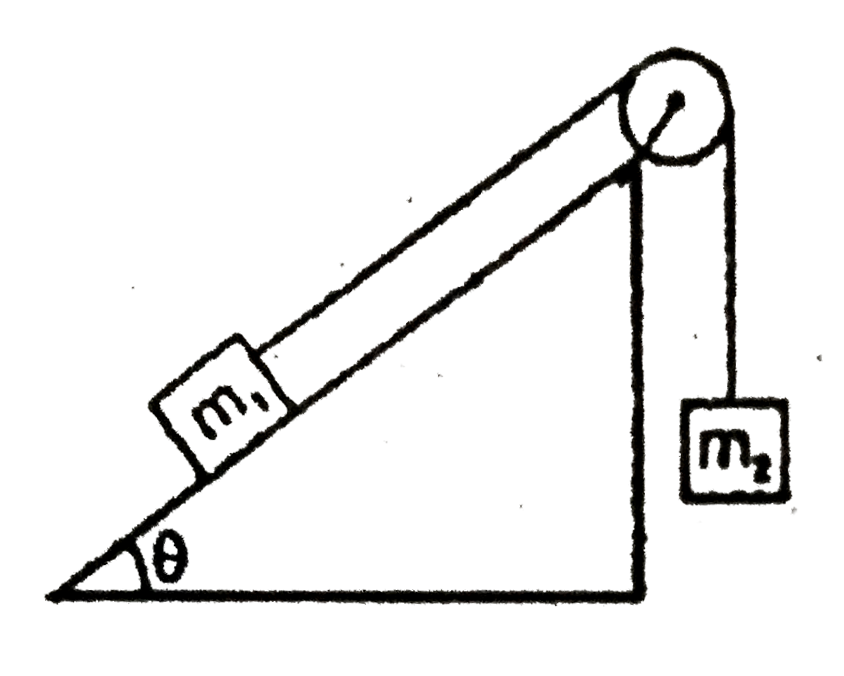
if m1=10kg,m2=5kg,θ=30∘, what is the acceleration of mass m2?
View SolutionTwo masses 6 kg and 4 kg are connected by massless flexible and inextensible string passing over massless and frictionless pulley.The acceleration of centre of mass is (g=10ms^2)
View Solution
