Two masses of 3 kg and 4 kg are connected at the two ends of a light inextensible string that passes over a frictionless pulley. Find the acceleration of the masses and the tension in the string, when the masses are released.
To solve the problem of two masses connected by a string over a frictionless pulley, we will follow these steps:
Step 1: Identify the masses and their weights
Let:
- Mass M1=3kg
- Mass M2=4kg
- Acceleration due to gravity g=10m/s2
Step 2: Write the equations of motion for both masses
For mass M1 (3 kg):
- The forces acting on it are the tension T in the string acting upwards and the weight M1g acting downwards.
- According to Newton's second law:
T−M1g=M1a(Equation 1)
For mass M2 (4 kg):
- The forces acting on it are the tension T acting upwards and the weight M2g acting downwards.
- According to Newton's second law:
M2g−T=M2a(Equation 2)
Step 3: Substitute the values into the equations
Substituting M1=3kg and M2=4kg into the equations:
From Equation 1:
T−3g=3a⇒T−3×10=3a⇒T−30=3a⇒T=3a+30(Equation 3)
From Equation 2:
4g−T=4a⇒4×10−T=4a⇒40−T=4a⇒T=40−4a(Equation 4)
Step 4: Set the equations for tension equal to each other
Now, we can set Equation 3 equal to Equation 4:
3a+30=40−4a
Step 5: Solve for acceleration a
Rearranging the equation:
3a+4a=40−30
7a=10
a=107m/s2≈1.43m/s2
Step 6: Substitute a back to find tension T
Now, substitute a back into Equation 3 or Equation 4 to find T. Using Equation 3:
T=3(107)+30
T=307+30=307+2107=2407N≈34.29N
Final Results
- The acceleration a of the masses is 107m/s2 or approximately 1.43m/s2.
- The tension T in the string is 2407N or approximately 34.29N.
Let:
- Mass M1=3kg
- Mass M2=4kg
- Acceleration due to gravity g=10m/s2
For mass M1 (3 kg):
- The forces acting on it are the tension T in the string acting upwards and the weight M1g acting downwards.
- According to Newton's second law:
T−M1g=M1a(Equation 1)
- The forces acting on it are the tension T acting upwards and the weight M2g acting downwards.
- According to Newton's second law:
M2g−T=M2a(Equation 2)
Substituting M1=3kg and M2=4kg into the equations:
T−3g=3a⇒T−3×10=3a⇒T−30=3a⇒T=3a+30(Equation 3)
4g−T=4a⇒4×10−T=4a⇒40−T=4a⇒T=40−4a(Equation 4)
Now, we can set Equation 3 equal to Equation 4:
3a+30=40−4a
Rearranging the equation:
3a+4a=40−30
7a=10
a=107m/s2≈1.43m/s2
Now, substitute a back into Equation 3 or Equation 4 to find T. Using Equation 3:
T=3(107)+30
T=307+30=307+2107=2407N≈34.29N
- The acceleration a of the masses is 107m/s2 or approximately 1.43m/s2.
- The tension T in the string is 2407N or approximately 34.29N.
Similar Questions
Two masses 8 kg and 12 kg are connected at the two ends of a light in extensible string that passes over a friction less pulley. Find the acceleration of the masses and tension in the string , when the masses are released
 .
.
View SolutionTwo masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
View Solution
Knowledge Check
Two masses 8 kg and 12 kg are connected at the two ends of a light in extensible string that passes over a friction less pulley Find the acceleration of the masses and tension in the string , when the masses are released
 . Ag4Bg5Cg8Dg6
. Ag4Bg5Cg8Dg6Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
Two masses 2 kg and 4 kg are connected at two ends of light inextensible string passing over a frictionless pulley . If the masses are released , then find the accelaration of the masses and the tension in the string .
View SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionTwo masses 6 kg and 4 kg are connected by massless flexible and inextensible string passing over massless and frictionless pulley.The acceleration of centre of mass is (g=10ms^2)
View SolutionTwo masses of 10 kg and 20 kg are connected with an inextensible string passing over two smooth pulleys as shown in the figure. The acceleration of 20 kg mass will be :
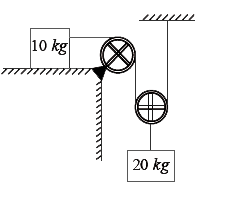
View SolutionTwo unequal masses are connected by a very light string over a clamped light smooth pulley. Find the acceleration of the system and the tension in the string.
View SolutionTwo masses M and M/ 2 are joint together by means of a light inextensible string passes over a frictionless pulley as shown in figure. When bigger mass is released the small one will ascend with an acceleration of
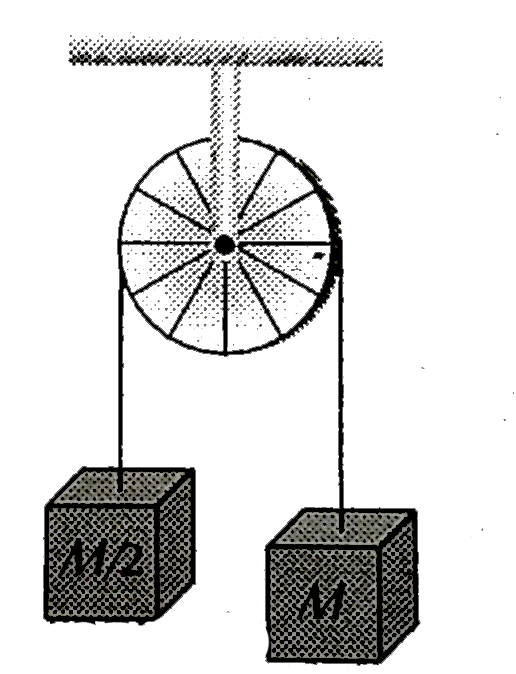
View Solution
