Two nonideal batteries are connected in parallel. Consider the following statements:
(A)The equivalent emf is smaller than either of the two emfs.
(B) The equivalent internal resistance is smaller than either of the two internal resistances.
(a)Both A and B are correct
(b)A is correct but B is worng
(c )B is correct but A is worng
(d)Both A and B are worng
The correct Answer is:C
To solve the question regarding the two non-ideal batteries connected in parallel and evaluate the statements about their equivalent EMF and internal resistance, we will follow these steps:
1. Understanding the Configuration:
- We have two non-ideal batteries connected in parallel. Let’s denote their EMFs as E1 and E2, and their internal resistances as r1 and r2.
2. Calculating the Equivalent EMF:
- For batteries in parallel, the formula for the equivalent EMF (Eeq) is given by:
Eeq=E1r1+E2r2r1+r2
- This equation shows that the equivalent EMF is a weighted average of the individual EMFs, influenced by their internal resistances.
3. Analyzing Statement A:
- We need to determine if Eeq<E1 and Eeq<E2.
- From the formula, since both E1 and E2 are in the numerator and r1 and r2 are positive values, it can be concluded that:
Eeq>E1andEeq>E2
- Therefore, Statement A is incorrect.
4. Calculating the Equivalent Internal Resistance:
- For internal resistances in parallel, the equivalent internal resistance (req) is calculated using:
1req=1r1+1r2
- This implies:
req<r1andreq<r2
- Hence, Statement B is correct.
5. Conclusion:
- Based on the analysis:
- Statement A is incorrect.
- Statement B is correct.
- Therefore, the correct answer is that A is incorrect, B is correct.
Final Answer:
The answer to the question is: A is incorrect, B is correct.
- We have two non-ideal batteries connected in parallel. Let’s denote their EMFs as E1 and E2, and their internal resistances as r1 and r2.
- For batteries in parallel, the formula for the equivalent EMF (Eeq) is given by:
Eeq=E1r1+E2r2r1+r2
- This equation shows that the equivalent EMF is a weighted average of the individual EMFs, influenced by their internal resistances.
- We need to determine if Eeq<E1 and Eeq<E2.
- From the formula, since both E1 and E2 are in the numerator and r1 and r2 are positive values, it can be concluded that:
Eeq>E1andEeq>E2
- Therefore, Statement A is incorrect.
- For internal resistances in parallel, the equivalent internal resistance (req) is calculated using:
1req=1r1+1r2
- This implies:
req<r1andreq<r2
- Hence, Statement B is correct.
- Based on the analysis:
- Statement A is incorrect.
- Statement B is correct.
- Therefore, the correct answer is that A is incorrect, B is correct.
The answer to the question is: A is incorrect, B is correct.
Topper's Solved these Questions
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - objective 2
9 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - Exercises
84 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - worked out Example
33 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
Similar Questions
the two nonideal batteries are connected in series. Consider the following statements :
(A)The equivalent emf is larger than either of the two emfs.
(B) the equivalent internal resistances is smaller than either of the two internal resistances.
View Solutionthe nonideal batteries are connected in series. Consider the following statements :
(A)The equivalent emf is larger than either of the two emfs.
(B) the equivalent internal resistances is smaller than either of the two internal resistances.
View Solution
Knowledge Check
If n cells each of emf E and internal resistance rare connected in parallel, then the total emf and internal resistances will be
Aε,rnBε,nrCnε,rnDnε,nr
Assertion : Two non-ideal batteries are connected in parallel with same polarities on same: side. The equivalent emf is smaller than either of the two emfs.
Reason : Two non-ideal batteries are connected in parallel, the equivalent inter resistance is smaller than either of the two internal resistances.
View SolutionIf three cell are connected in parallel then equivalent emf……. and equivalent internal resistance is …..
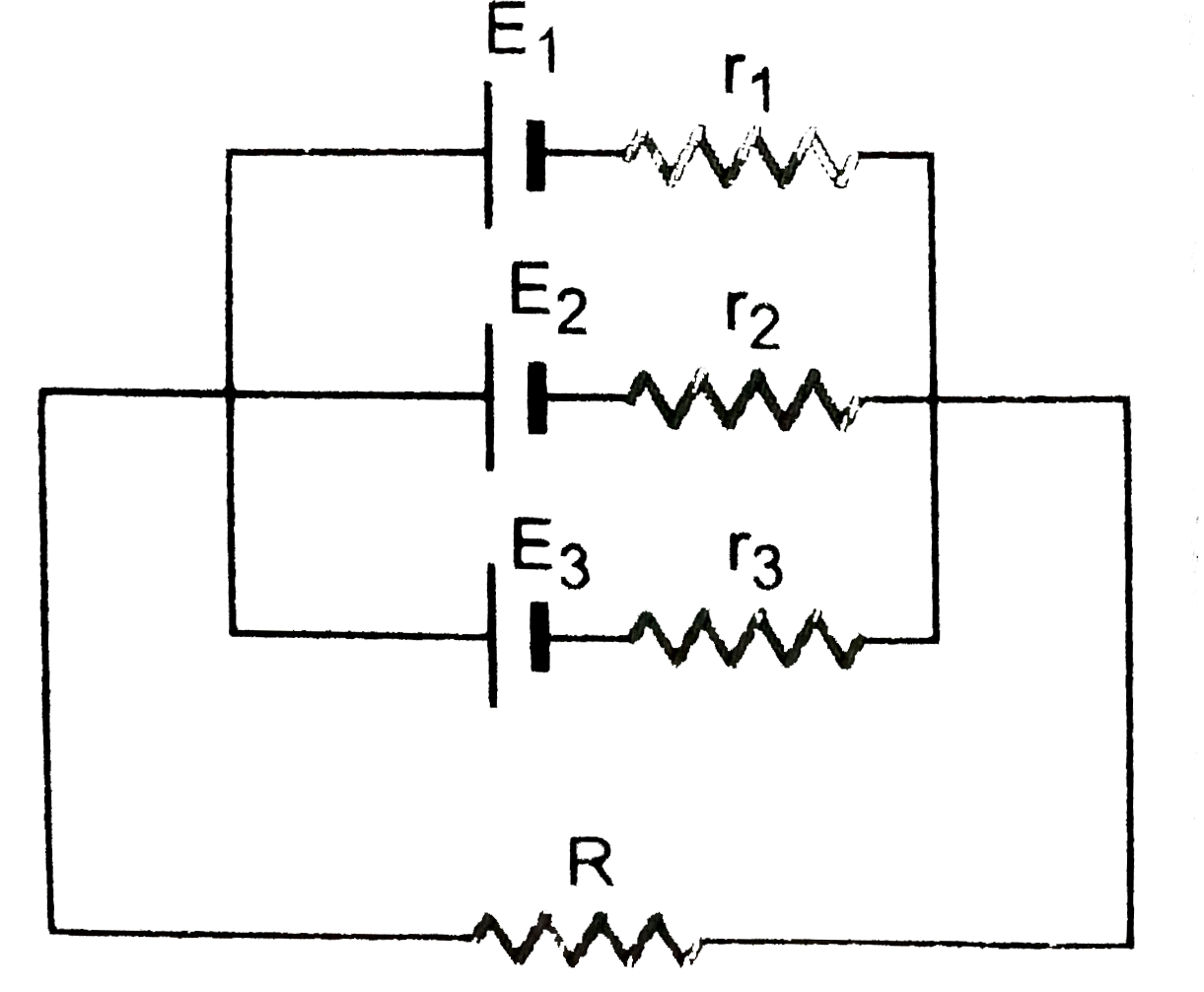
View SolutionState how are the two resistors joined with a battery in each of the following cases when :
equivalent resistance is more than either of the two resistances.
View SolutionState how are the two resistors joined with a battery in each of the following cases when :
equivalent resistance is less than either of the two resistances,
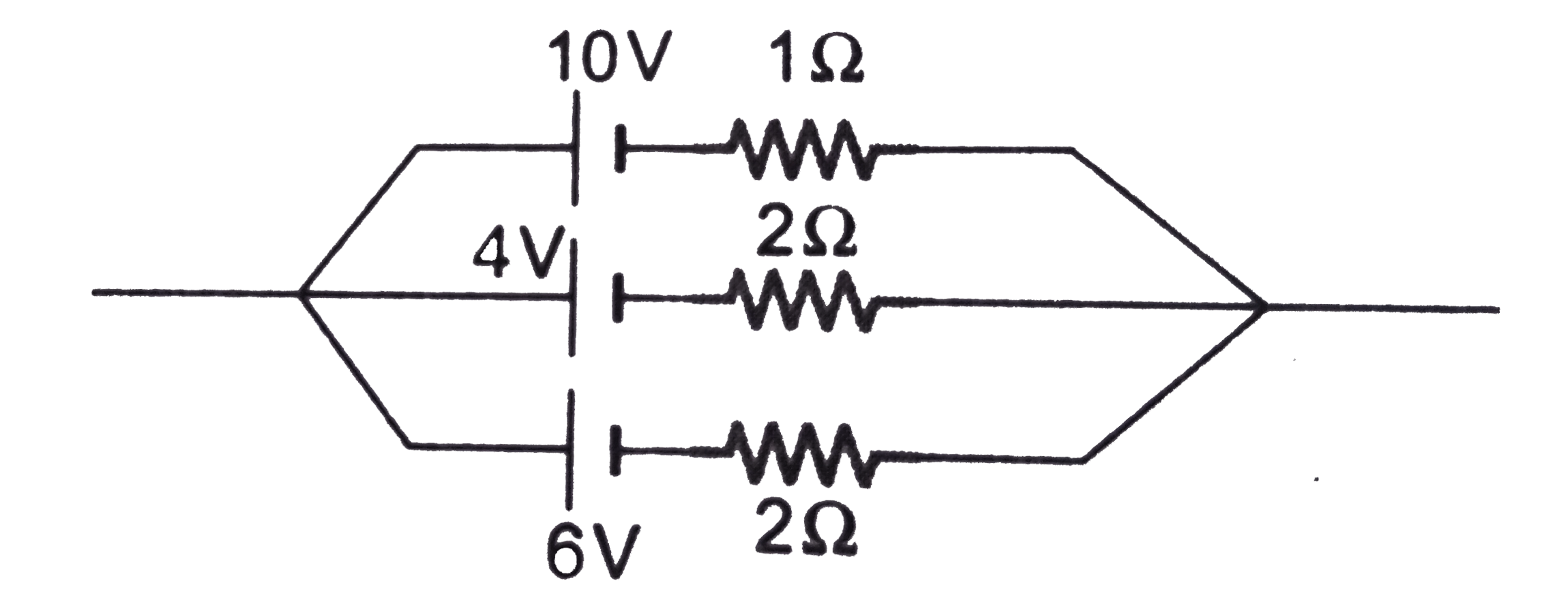
View SolutionFind the equivalent emf and internal resistance of the arrangement shown in figure.
View SolutionThe equivalent resistance of two resistor connected in series is 6Ω and their equivalent resistance is 43Ω. What are the values of resistances ?
View SolutionTwo cells of e.m.f. 10V & 15V are connected in parallel to each other between points A&B. The cell of e.m.f. 10V is ideal but the cell of e.m.f. 15V has internal resistance 1Ω. The equivalent e.m.f. between A and B is:

View Solution
