Two particles of different masses are thrown simultaneously in air. Centre of mass of two balls while both are in mid air.
Move in a straight line independent of initial velocities of particles
Move in straight line when both the particles are thrown along same vertical line
Have acceleration equal to g
Have acceleration depending on initial velocities of particles
The correct Answer is:B, C
To solve the problem of finding the behavior of the center of mass of two particles of different masses thrown simultaneously in the air, we can analyze the situation step by step.
1. Understanding the System:
We have two particles with different masses, m1 and m2. They are thrown simultaneously into the air. We need to determine the motion of their center of mass.
2. Defining the Center of Mass:
The center of mass (CM) of a system of particles is given by the formula:
CM=m1⋅x1+m2⋅x2m1+m2
where x1 and x2 are the positions of the two particles.
3. Analyzing the Motion:
- If both particles are thrown at the same angle and with different velocities, they will follow parabolic trajectories due to the influence of gravity.
- The center of mass will also follow a parabolic path, but its trajectory will depend on the relative masses and initial velocities of the two particles.
4. Special Case - Vertical Throw:
- If both particles are thrown vertically (along the same vertical line), the center of mass will move in a straight line. This is because both particles are subjected to the same gravitational force and will have the same vertical motion.
5. Acceleration of the Center of Mass:
- The only external force acting on the system is the gravitational force. This means that the acceleration of the center of mass will be equal to g (acceleration due to gravity), regardless of the initial velocities of the particles.
6. Conclusion:
- The center of mass of the two particles moves in a straight line when both are thrown vertically.
- The center of mass has an acceleration equal to g, independent of the initial velocities of the particles.
Final Answer:
- The correct statements regarding the center of mass of the two particles while both are in mid-air are:
- It moves in a straight line when both particles are thrown along the same vertical line.
- It has an acceleration equal to g.
We have two particles with different masses, m1 and m2. They are thrown simultaneously into the air. We need to determine the motion of their center of mass.
The center of mass (CM) of a system of particles is given by the formula:
CM=m1⋅x1+m2⋅x2m1+m2
where x1 and x2 are the positions of the two particles.
- If both particles are thrown at the same angle and with different velocities, they will follow parabolic trajectories due to the influence of gravity.
- The center of mass will also follow a parabolic path, but its trajectory will depend on the relative masses and initial velocities of the two particles.
- If both particles are thrown vertically (along the same vertical line), the center of mass will move in a straight line. This is because both particles are subjected to the same gravitational force and will have the same vertical motion.
- The only external force acting on the system is the gravitational force. This means that the acceleration of the center of mass will be equal to g (acceleration due to gravity), regardless of the initial velocities of the particles.
- The center of mass of the two particles moves in a straight line when both are thrown vertically.
- The center of mass has an acceleration equal to g, independent of the initial velocities of the particles.
- The correct statements regarding the center of mass of the two particles while both are in mid-air are:
- It moves in a straight line when both particles are thrown along the same vertical line.
- It has an acceleration equal to g.
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS) )
10 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (MATCHING TYPE QUESTIONS) )
3 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )
48 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
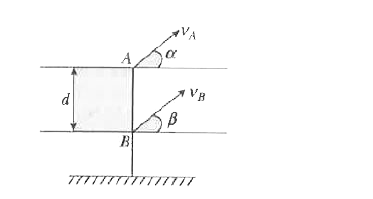
Two particles A and B are thrown simultaneously from two different floors of tower having distance d between them.Velocitiy of particle A is vA at angle α from horizontal while velocity of particle B is vB at an angle β from horizontal.If two particles collide in mid-air,then find vAvB.
View SolutionThe centre of mass of two particles system lies
View Solution
Knowledge Check
Two balls are thrown simultaneously in air. The acceleration of the centre of mass of the two balls while in air
Adepends on the direction of the motion of the ballsBdepends on the masses of the two ballsCdepends on the speeds of the two ballsDis equla to gTwo balls are thrown simultaneously in air. The acceleration of the centre of mass of the two balls while in air
Ais equal to g (Acceleration due to gravity)Bdepends on the masses of the two ballsCdepends on the direction of motion of the two balls.Ddepends on the speeds of the two balls.Two stones of different masses are dropped simultaneously from the top of a building
ASmaller stone hit the ground earlierBLarger stone hit the ground earlierCBoth stones reach the ground simultaneouslyDWhich of the stones reach the ground earlier depends on the
Two particles of different masses collide head on. Then for the system
View SolutionTwo balls of different masses have the same kinetic energy. Then the
View SolutionTwo balls of different masses are thrown in air with different velocities. While they are in air acceleration of centre of mass of the system. (neglect air resistance)?
View SolutionTwo bodies of different masses are dropped simultaneously from the top of a tower. If air resistance is proportional to the mass of the body then,
View SolutionTwo particles A and B are thrown simultaneously from two different floors of tower having distance d between them. Velocities of particle A is vA at angle α from horizontal while velocities of particle B is vB at an angle β from horizontal. If two particles collide in mid-air, then vAvB.
View Solution
