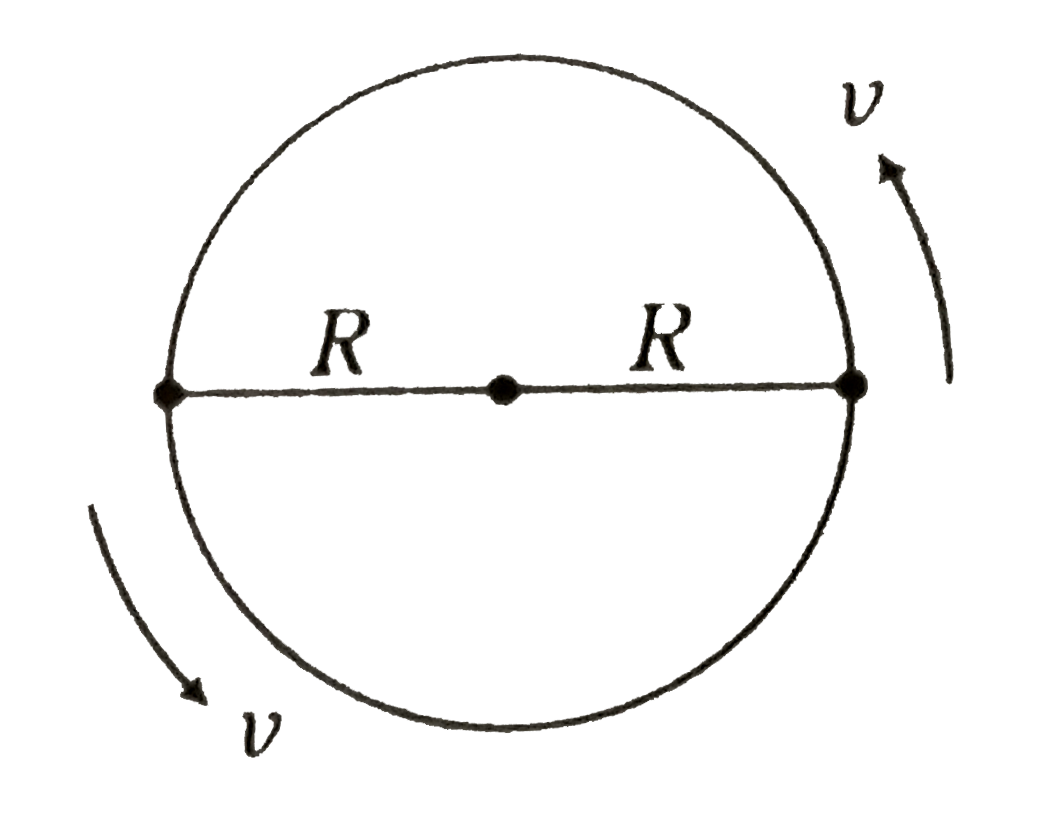
Two particles of equal mass (m) each move in a circle of radius (r) under the action of their mutual gravitational attraction find the speed of each particle.

A

$v = \sqrt{\frac{G m}{R}}$

B

$v = \sqrt{\frac{G m}{2 R}}$

C

$v = \frac{1}{2} \sqrt{\frac{G m}{R}}$

D

$v = \sqrt{\frac{4 G m}{R}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

As gravitational force provides the centripetal force to the satellite to revolve around the earth

$\frac{G . m . m}{4 R^{2}} = \frac{m v^{2}}{(R)} \Rightarrow v = \frac{1}{2} \sqrt{\frac{G m}{R}}$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two particles of equal mass m go around a circle of radius R under the action the of their mutual gravitational attraction . The speed v of each particle is
A $\frac{1}{2} \sqrt{\frac{G m}{R}}$
B $\sqrt{\frac{4 G M}{R}}$
C $\frac{1}{2 R} \sqrt{\frac{1}{G m}}$
D $\sqrt{\frac{G m}{2 R}}$
Question 2 - Select One
Two particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of earth particle is
A $\frac{1}{3} \sqrt{\frac{G m}{R}}$
B $\frac{1}{2} \sqrt{\frac{G m}{R}}$
C $\frac{1}{2} \sqrt{\frac{R}{G m}}$
D $\sqrt{\frac{G m}{R}}$
Question 3 - Select One
Two particles of equal mass $' m'$ go around a circle of radius $R$ under the action of their mutual gravitaitonal attraction. The speed of each particle with respect to their centre of a mass is -
A $\sqrt{\frac{G m}{4 R}}$
B $\sqrt{\frac{G m}{3 R}}$
C $\sqrt{\frac{G m}{2 R}}$
D $\sqrt{\frac{G m}{R}}$

DC PANDEY-GRAVITATION-(A) Chapter Exercises

Home
Ask Doubt
Profile