Two positive charges of magnitude 'q' are placed at the ends of a side (side 1 ) of a square of side 2a . Two negative charges of the same magnitude are kept at the other corners . Starting from rest , if a charge Q moves from the middle of side 1 to the centre of square , its kinetic energy at the centre of square is :
zero
14πε02qQa(1+1√5)
14πε02qQa(1−1√5)
14πε02qQa(1−1√5)
The correct Answer is:D
Work done on charge Q = change in K.E = Ef−Ef=Ef−0
∴Q(VA−VB)=Ef
Q(24πε0qa−24πε0q√5a−0)=Ef
∴E6=2qQ4πε0a(1−1√5)
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - RECENT COMPETITIVE QUESTIONS39videos
ELECTROSTATICS
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - LEVEL -II74videos
ELECTROSTATICS
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTRONS & PHOTONSEXERCISE - RECENT COMPETITIVE QUESTIONS20videos
ELECTRONS & PHOTONS
- BOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Recent Competitive Questions8videos
GRAVITATION
Similar Questions
Two positive charges of magnitude q are placed at the ends of a side ( side 1) of a square of side 2a . Two negative charges of the same magnitude are kept at the other corners . Staring from rest , a charge Q moves from the middle of side 1 to the centre of square , its kinetic energy at the centre of square is -.
View SolutionThree positive charges of equal magnitude q are placed at the vertics of and equilatral triangle of side l. How can the system of charges be palced in equilibrium?
View Solution
Knowledge Check
- Question 1 - Select One
Two positive charges of magnitude q are placed at the ends of a side ( side 1) of a square of side 2a . Two negative charges of the same magnitude are kept at the other corners . Staring from rest , n a charge Q moves from the middle of side 1 to the centre of square , its kinetic energy at the centre of square is -.
A14π∈02qQa(1+1√5)B14π∈02qQa(1+1√5)C14π∈02qQa(1+1√5)D14π∈02qQa(1+1√5) - Question 2 - Select One
Two positive charges of magnitude q are placed at the ends of a side (side 1 ) of square of side 2a. Two negative cahrges of the same magnitude ar kept at the other comers. Starting from rest, if the charge Q moves from the middle of side (1) to the centre of square , its kinetc energy at the centre of square is
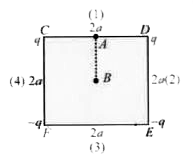 A14π∈02qQa(1−1√5)BzeroC14π∈02qQa(1+1√5D14π∈02qQa(1−2√5)
A14π∈02qQa(1−1√5)BzeroC14π∈02qQa(1+1√5D14π∈02qQa(1−2√5) - Question 3 - Select One
Three positive charges of equal magnitude q are placed at the vertices of and equilateral triangle of side l. How can the system of charges be placed in equilibrium?
Aby placing a charge Q=−q/√3 at the centroid of the triangleBby placing a charge Q=q/√3 at the centroid of the triangleCby placing a charge Q=q at the centroid of the triangleDby placing a charge Q=−q at the centroid of the triangle
Four charges of +q, +q +q and +q are placed at the corners A, B, C and D of s square. The resultant force on the charge at D
View SolutionFour charges of same magnitude and same sign are placed at the corners of a square, of each side0⋅1m. What is electric field intensity at the center of the square?
View SolutionThree charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
View SolutionThree charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
View SolutionThree charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
View Solution

