Two solid spherical planets of equal radii R having masses 4M and 9M their centre are separated by a distance 6R. A projectile of mass m is sent from theplanet of mass 4 M towards the heavier planet. What is the distance r of the point from the lighter planet where the gravitational force on the projectille is zero ?
1.4R
1.8R
1.5R
2.4R
The correct Answer is:D
The gravitational force on projectile of mass m at a distance r (at A) from the planet of mass 4M is zero.
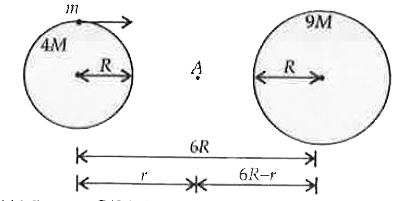
∴G(4M)mr2=G(9M)m(6R−r)2
or 4(6R−r)2=9r2 or 2(6R−r)=3r or r=2.4R
Topper's Solved these Questions
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - NEET CAFE TOPICWISE PRACTICE QUESTIONS (ACCELERATION DUE TO GRAVITY AND ITS VARIATION WITH ALTITUDE AND DEPTH)
19 Videos
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - NEET CAFE TOPICWISE PRACTICE QUESTIONS (GRAVITATIONAL POTENTIAL ENERGY AND GRAVITATIONAL POTENTIAL)
6 Videos
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - NEET CAFE TOPICWISE PRACTICE QUESTIONS (KEPLER.S LAWS OF PLANETARY MOTION)
9 Videos
- BEHAVIOUR OF PERFECT GAS AND KINETIC THEORYBOOK - MTG GUIDECHAPTER - BEHAVIOUR OF PERFECT GAS AND KINETIC THEORYEXERCISE - AIPMT / NEET (MCQs)
11 Videos
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - AIPMT/ NEET MCQs
31 Videos
Similar Questions
Two solid spherical planets of equal radii R have masses 4M and 9M. Their centres are scparated by a distance 6R. A projectile of mass m is sent from the planet of mass 4M towards the heavier planet. If the distance r of the point from the lighter planet where the gravitational 'force on the projectile is zero is kR, then calculate k.
View SolutionTwo uniform solid spheres of equal radii R, but mass M. and 4M have a centre to centre separation 6R, as shown in the figure. The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the center of the second sphere. If the minimum speed v of the projectile so that it reaches the surface of the second sphere is √xGMyR, then find (x,+y).
'(##CEN_KSR_PHY_JEE_C10_038_Q05##)'
View Solution
Knowledge Check
Two point masses m and M are separated by a distance L . The distance of the centre of mass of the system from m is
AL(m/M)BL(M/m)CL(Mm+M)DL(mm+M)Two point masses m and M are separated bya distance L . The distance of the centre of mass of the system from m is
AL(m/M)BL(M/m)CL(Mm+M)DL(mm+M)Two bodies of masses m and 4m are placed at a distance r. The gravitational potential at a point on the line joining them where the gravitational field is zero is:
AzeroB−4GmrC−6GmrD−9Gmr
Two bodies of masses m1 and m2 are separated by a distance R. The distance of the centre of mass of the bodies from the mass m1 is
View SolutionTwo bodies of masses m1 and m2 are separated by a distance R. The distance of the centre of mass of the bodies from the mass m1 is
View SolutionTwo bodies of masses m and 4m are placed at a distance r. The gravitational potential at a point on the line joining them where the gravitational field is zero is:
View SolutionTwo bodies of masses m and 4 m are placed at a distance r. The gravitational potential at a point on the line joining them where the gravitational field is zero, is
View SolutionTwo point masses m and 4 m are seperated by a distance d on a line . A third point mass m0 is to be placed at a point on the line such that the net gravitational force on it zero .

The distance of that point from the m mass is
View Solution
