Two thin planks are moving on a four identical cylinders as shown. There is no slipping at any contact points. Calculate the ratio of angular speed of upper cylinder to lower cylinder
The correct Answer is:3
Step by step video, text & image solution for Two thin planks are moving on a four identical cylinders as shown. There is no slipping at any contact points. Calculate the ratio of angular speed of upper cylinder to lower cylinder by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Matrix Matching Type Questions
17 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
Consider a cylinder of mass M and radius R lying on a rough horizontal plane. It has a plank lying on its top as shown in figure. A force F is applied on the plank such that the plank moves and causes the cylinder to roll the plank always remains horizontal. there is no slipping at any point of contact. Calculate the acceleration of the cylinder and the frictional forces at the two contact.
View SolutionConsider a cylinder of mass M and radius R lying on a rough horizontal plane. It has a plank lying on its top as shown in the figure. A force F is applied on the plank such that the plank moves and causes the cylinder to roll. The plank always remains horizontal. There is no slipping at any point to contact.
(a) what are the directions of the fricition forces acting at A and B on the plank and the cylinder ?
(b) Calculate the acceleration of the cylinder.
(c) Find the value of frictional force at A & B.
View Solution
Knowledge Check
A system of identical cylinders and plates is shown in Fig. All the cylinders are identical and there is no slipping at any contact. The velocity of lower and upper plates are V and 2V, respectively, as shown in Fig. Then the ratio of angular speeds of the upper cylinders to lower cylinders is
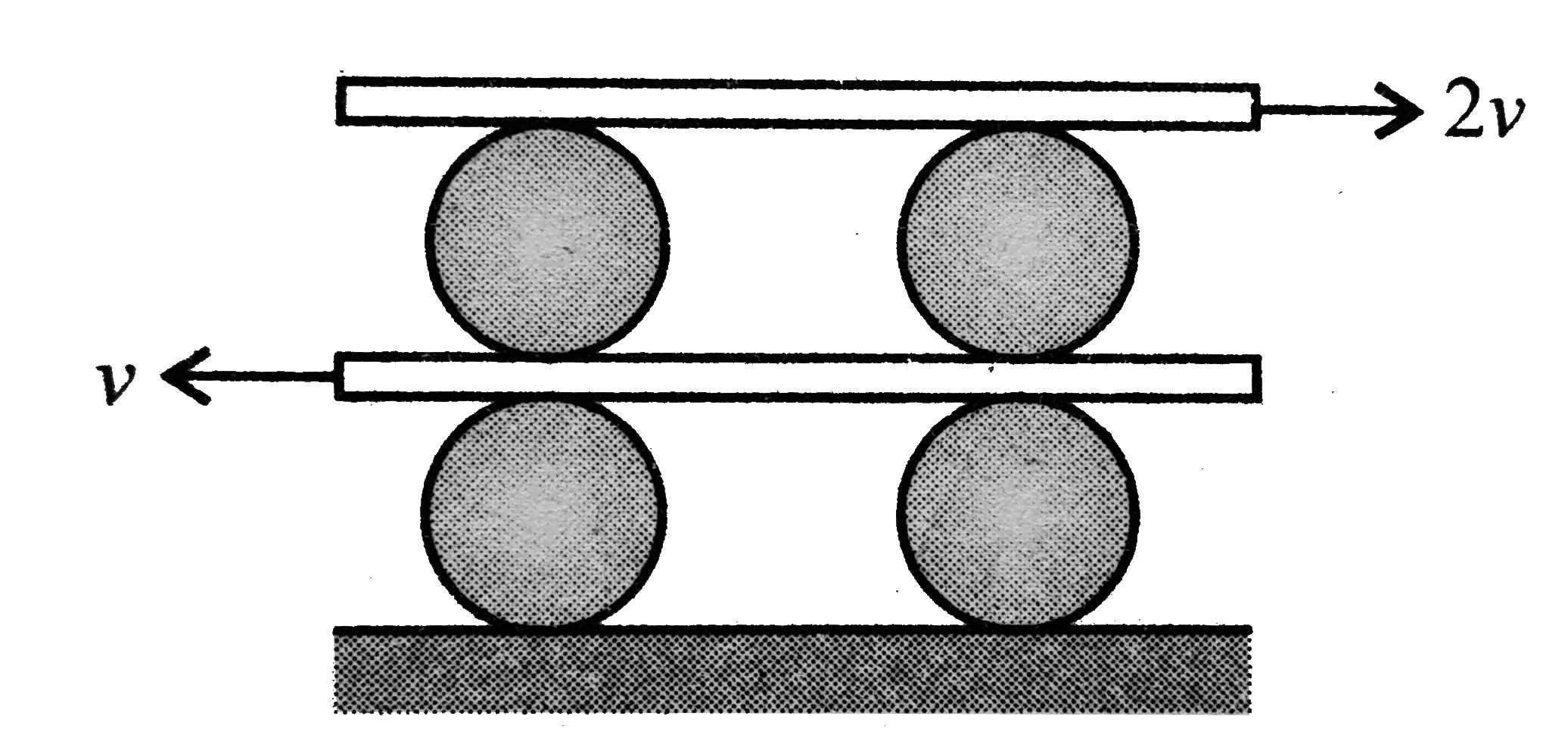A13B3C1Dnone of the aboveA plank P is placed on a solid cylinder S, which rolls on a horizontal surface. The two are of equal mass. There is no slipping at any of the surfaces in contact. The ratio of kinetic energy of P to the kinetic energy of S is:
A1:1B2:1C8:3D11:8Consider a cylinder of mass M=1kg and radius R=1mlying on a rough horizontal plane. It has a plank lying on its stop as shown in the figure.
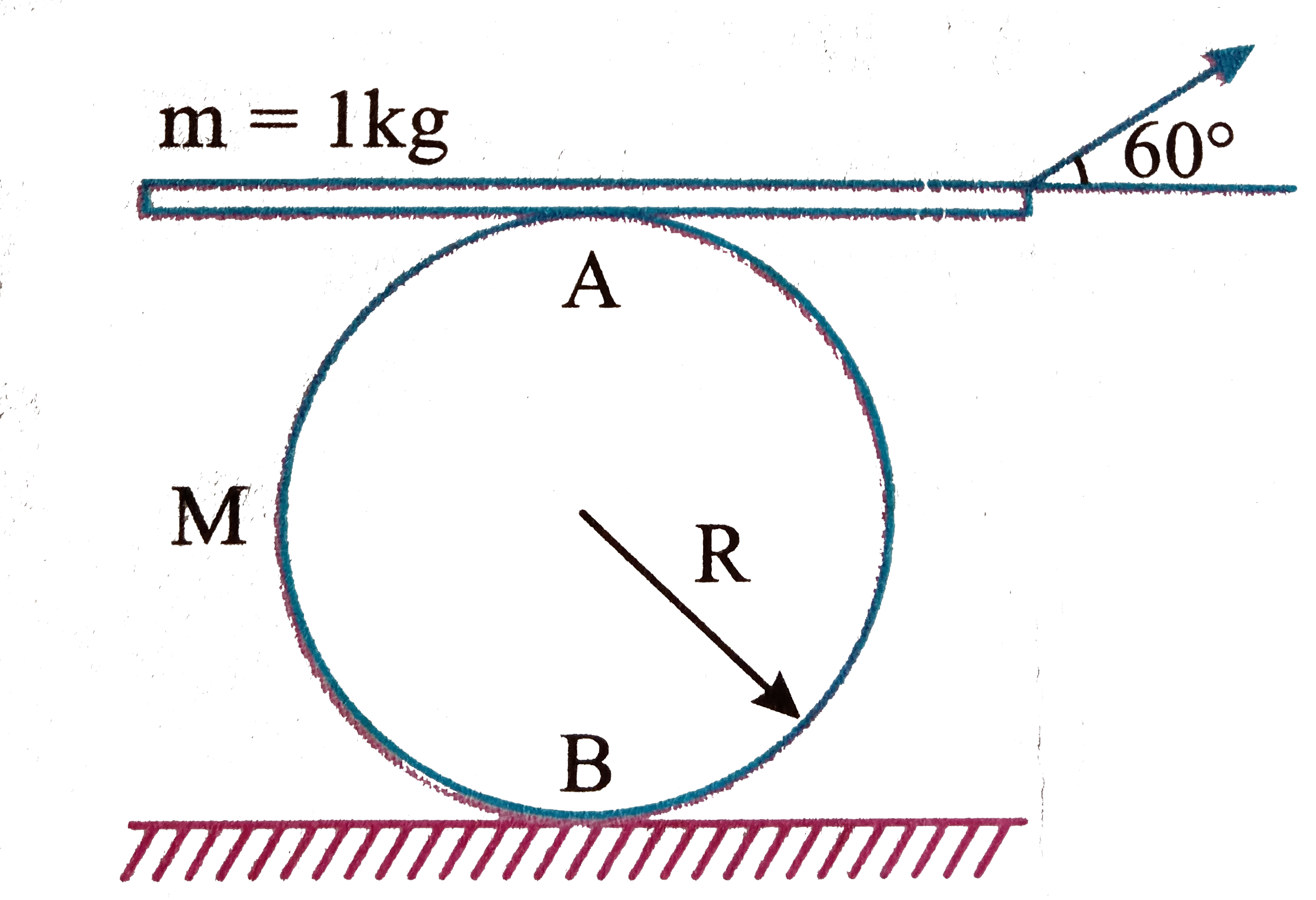
A force F=55N is applied on the plank moves and causes the cylinder to roll. The plank always remains horizontal. there is no slipping at any point of contact.
The acceleration of cylinder isA20m/s2B10m/s2C5m/s2D12m/s2
AB is a non uniform plank of length L=4R with its centre of mass at C such that AC=R. It is placed on a step with its one end A supported by a cylinder of radius R as shown in figure. The centre of mass of the plank is just outside the edge of the step. The cylinder is slowly rolled on the lower step such that there is no slipping at any of its contacts. Calculate the distance through which the centre of the cylinder moves before the plank loses contact with the horizontal surface of the upper step.
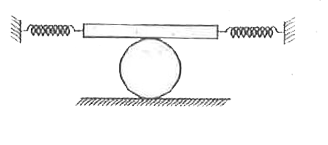
View SolutionIn the figure shown, mass of the plank is m and that of the solid cylinder is 8m. Springs are light. The plank is slightly displaced from equilibrium and then released. Find the period of small oscillations (in seconds) of the plank. There is no slipping at any contact point. The ratio of the mass of the plank adn stiffness of the spring i.e., mK=2π2
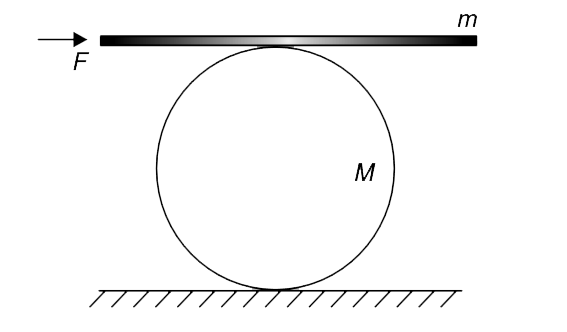
View SolutionA boy pushes a cylinder of mass M with the help of a plank of mass m as shown in figure. There is no slipping at any contact. The horizontal component of the force applied by the boy on the plank is F. Find
(a) The acceleration of the centre of the cylinder
(b) The friction force between the plank and the cylinder
View SolutionA solid cylinder of mass M and radius 2R is rolled up on an incline with the help of a plank of mass 2M as shown in the figure. A constant force F is acting on the plank parallel to the incline. There is no slipping at any of the contact. The friction force between the plank and cylinder is given by:
View SolutionConsider a cylinder of mass M=1kg and radius R=1mlying on a rough horizontal plane. It has a plank lying on its stop as shown in the figure.
A force F=55N is applied on the plank moves and causes the cylinder to roll. The plank always remains horizontal. there is no slipping at any point of contact.
The value of frictional force at A is
View Solution