Two very long straight parallel wires carry steady currents i and 2i in opposite directions. The distance between the wires is d. At a certain instant of time a point charge q is at a point equidistant from the two wires in the plane of the wires. Its instantaneous velocity →v is perpendicular to this plane. The magnitude of the force due to the magnetic field acting on t he charge at this instant is
μ0iqv2πd
μ0iqvπd
3μ0iqv2πd
zero
The correct Answer is:D
To solve the problem, we need to determine the magnetic force acting on a point charge q that is located equidistant from two long parallel wires carrying currents i and 2i in opposite directions. The charge is moving with a velocity →v that is perpendicular to the plane of the wires.
1. Identify the Magnetic Fields:
- The magnetic field B created by a long straight wire carrying current I at a distance r from the wire is given by the formula:
B=μ0I2πr
- For the two wires, the magnetic fields at the point where the charge is located (which is equidistant from both wires) will be calculated.
2. Determine the Direction of Magnetic Fields:
- For the wire carrying current i (let's say it is on the left), the magnetic field at the point will be directed into the plane (using the right-hand rule).
- For the wire carrying current 2i (on the right), the magnetic field at the same point will also be directed into the plane.
- Since both currents are in opposite directions, the magnetic fields at the point will add up.
3. Calculate the Total Magnetic Field:
- Let the distance from each wire to the point charge be r=d2.
- The magnetic field due to the wire with current i:
B1=μ0i2πd2=μ0iπd
- The magnetic field due to the wire with current 2i:
B2=μ0(2i)2πd2=μ0(2i)πd
- The total magnetic field B at the point is:
B=B1+B2=μ0iπd+μ0(2i)πd=3μ0iπd
4. Calculate the Magnetic Force on the Charge:
- The magnetic force →F on a charge q moving with velocity →v in a magnetic field →B is given by:
→F=q→v×→B
- Since the velocity →v is perpendicular to the plane of the wires and the magnetic field →B is directed into the plane, the angle θ between →v and →B is 90∘.
5. Magnitude of the Force:
- The magnitude of the force can be calculated as:
F=qvBsin(90∘)=qvB
- Substituting for B:
F=qv(3μ0iπd)
Final Answer:
The magnitude of the force due to the magnetic field acting on the charge q at this instant is:
F=3μ0qivπd
- The magnetic field B created by a long straight wire carrying current I at a distance r from the wire is given by the formula:
B=μ0I2πr
- For the two wires, the magnetic fields at the point where the charge is located (which is equidistant from both wires) will be calculated.
- For the wire carrying current i (let's say it is on the left), the magnetic field at the point will be directed into the plane (using the right-hand rule).
- For the wire carrying current 2i (on the right), the magnetic field at the same point will also be directed into the plane.
- Since both currents are in opposite directions, the magnetic fields at the point will add up.
- Let the distance from each wire to the point charge be r=d2.
- The magnetic field due to the wire with current i:
B1=μ0i2πd2=μ0iπd
- The magnetic field due to the wire with current 2i:
B2=μ0(2i)2πd2=μ0(2i)πd
- The total magnetic field B at the point is:
B=B1+B2=μ0iπd+μ0(2i)πd=3μ0iπd
- The magnetic force →F on a charge q moving with velocity →v in a magnetic field →B is given by:
→F=q→v×→B
- Since the velocity →v is perpendicular to the plane of the wires and the magnetic field →B is directed into the plane, the angle θ between →v and →B is 90∘.
- The magnitude of the force can be calculated as:
F=qvBsin(90∘)=qvB
- Substituting for B:
F=qv(3μ0iπd)
The magnitude of the force due to the magnetic field acting on the charge q at this instant is:
F=3μ0qivπd
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - More than One Option is Correct
25 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Comprehension type Questions
16 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Integer type Questions
10 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
- MEASUREMENT AND ERRORSBOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective
19 Videos
Similar Questions
Two very long, straight, parallel wires carry steady currents I and −I respectively.The distance between the wires is d.At a certain instant of time, a point charge q is at a point equidistant from the two wires,in the plane of wires.Its instantaneous velocity →v is perpendicular to this plane.The magnitude of the force due to the magnetic field acting on the charge at this instant is:
View SolutionTwo very long, straight , parallel wires carry steady currents I&−I respectively . The distance between the wires is d. At a certain instant of time, a point charge q is at a point equidistant from the wires , in the plane of the wires. Its instantaneous vel,ocity v is perpendicular to this plane. The magnitude of the force due to the magnetic field acting on the charge at this instant is
View SolutionThe two long, straight wires carrying electric currents in opposite directions. The separation between the wires is 5.0 cm. Find the magnetic field at a point P midway between the wires.
View SolutionIf current in two parallel wires flow in opposite directions, the force between the wires will:
View SolutionTwo long straight wires, each carrying a current I in opposite directions are separated by a distance R. The magnetic induction at a point mid way between the wire is
View SolutionTwo perpendicular infinite wires are carrying current i as shown in the figure. The magnetic field at point P is :
_2019_CBT2_E01_008_Q01.png)
View SolutionTwo long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
View SolutionIn Fig. two long parallel wires (seen end-on) that are a distance R apart carry equal currents i in the same sense. Find the magnitude of the magnetic field at point P , which lies quidistant from the two wires at an angle θ from the plane of the wires.

View SolutionIn fig. two long parallel wires carry equal currents in opposite directions. Point O is situated midway between the wires and X−Y plane contains the two wires and the position Z-axis comes normally out of the plane of paper. The magnetic field B at O is non-zero along
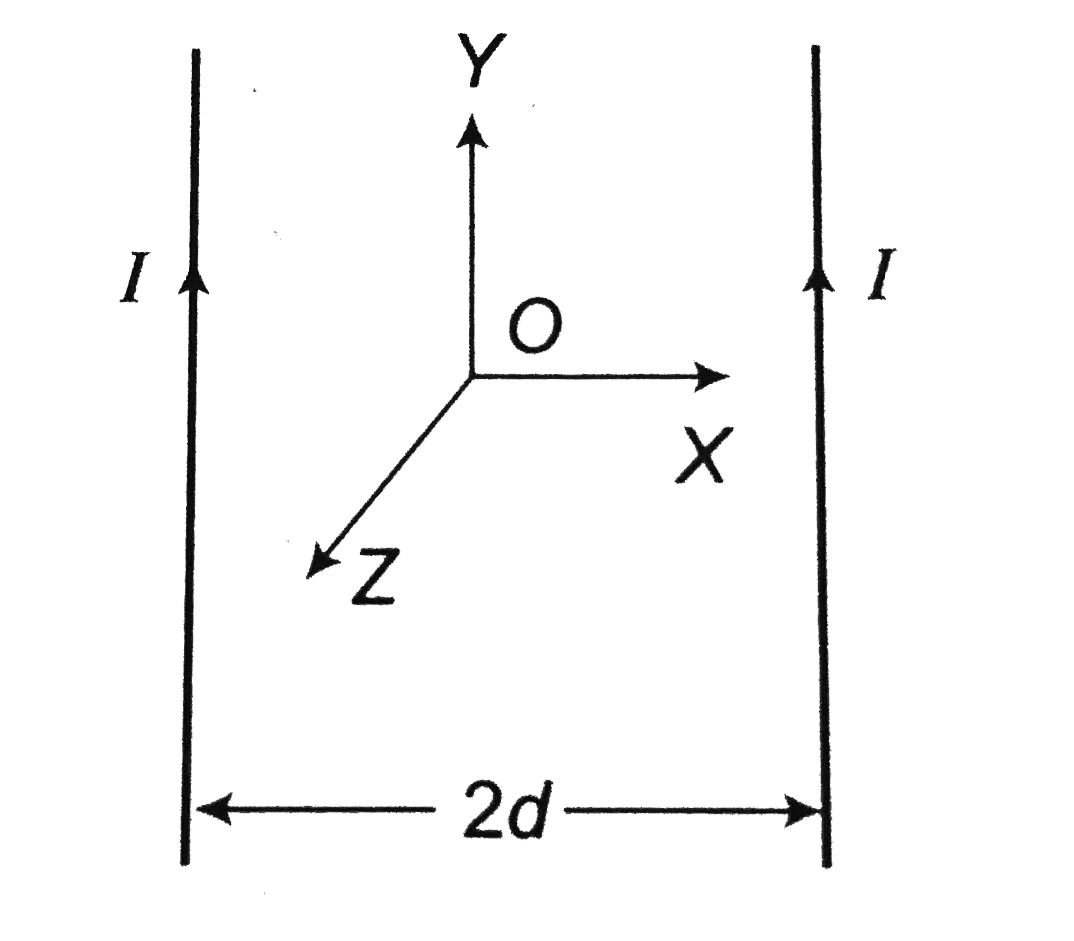
View SolutionTwo thin, long, parallel wires, separated by a distance 'd' carry a current of 'i' A in the same direction. They will
View Solution
