Two very long, straight , parallel wires carry steady currents I&−I respectively . The distance between the wires is d. At a certain instant of time, a point charge q is at a point equidistant from the wires , in the plane of the wires. Its instantaneous vel,ocity v is perpendicular to this plane. The magnitude of the force due to the magnetic field acting on the charge at this instant is
μ0Iqv2πd
μ0Iqvπd
2μ0Iqvπd
0
The correct Answer is:D
To solve the problem, we need to find the magnitude of the force acting on a point charge q due to the magnetic field created by two long parallel wires carrying currents I and −I respectively. The charge is located at a point equidistant from the wires, and its velocity is perpendicular to the plane of the wires.
1. Identify the Configuration:
- We have two long parallel wires. One wire carries a current I in the positive x-direction, and the other wire carries a current −I in the negative x-direction.
- The distance between the wires is d.
- The point charge q is located at the midpoint between the two wires, which is at a distance d2 from each wire.
2. Calculate the Magnetic Field at the Charge's Location:
- The magnetic field B due to a long straight current-carrying wire at a distance r is given by:
B=μ0I2πr
- For the wire carrying current I at a distance d2:
B1=μ0I2π(d2)=μ0Iπd
- For the wire carrying current −I at the same distance d2:
B2=μ0(−I)2π(d2)=−μ0Iπd
- The net magnetic field B at the midpoint (where the charge is located) is:
B=B1+B2=μ0Iπd−μ0Iπd=0
3. Determine the Force on the Charge:
- The magnetic force F on a charge q moving with velocity v in a magnetic field B is given by:
F=qvBsin(θ)
- Here, θ is the angle between the velocity vector v and the magnetic field B. Since B=0, the force becomes:
F=qv⋅0⋅sin(θ)=0
4. Conclusion:
- The magnitude of the force acting on the charge q due to the magnetic field created by the two wires is 0.
Final Answer:
The magnitude of the force due to the magnetic field acting on the charge at this instant is 0.
- We have two long parallel wires. One wire carries a current I in the positive x-direction, and the other wire carries a current −I in the negative x-direction.
- The distance between the wires is d.
- The point charge q is located at the midpoint between the two wires, which is at a distance d2 from each wire.
- The magnetic field B due to a long straight current-carrying wire at a distance r is given by:
B=μ0I2πr
- For the wire carrying current I at a distance d2:
B1=μ0I2π(d2)=μ0Iπd
- For the wire carrying current −I at the same distance d2:
B2=μ0(−I)2π(d2)=−μ0Iπd
- The net magnetic field B at the midpoint (where the charge is located) is:
B=B1+B2=μ0Iπd−μ0Iπd=0
- The magnetic force F on a charge q moving with velocity v in a magnetic field B is given by:
F=qvBsin(θ)
- Here, θ is the angle between the velocity vector v and the magnetic field B. Since B=0, the force becomes:
F=qv⋅0⋅sin(θ)=0
- The magnitude of the force acting on the charge q due to the magnetic field created by the two wires is 0.
The magnitude of the force due to the magnetic field acting on the charge at this instant is 0.
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Archives (multiple Correct )
1 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Archives (linked Comprehension)
4 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Archives (fill In The Blanks)
1 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
Two very long, straight, parallel wires carry steady currents I and −I respectively.The distance between the wires is d.At a certain instant of time, a point charge q is at a point equidistant from the two wires,in the plane of wires.Its instantaneous velocity →v is perpendicular to this plane.The magnitude of the force due to the magnetic field acting on the charge at this instant is:
View SolutionTwo very long straight parallel wires carry steady currents i and 2i in opposite directions. The distance between the wires is d. At a certain instant of time a point charge q is at a point equidistant from the two wires in the plane of the wires. Its instantaneous velocity →v is perpendicular to this plane. The magnitude of the force due to the magnetic field acting on t he charge at this instant is
View Solution
Knowledge Check
If a long straight wire carries a current of 40 A, then the magnitude of the field B at a point 15 cm away from the wire is
A5.34×10−5TB8.34×10−5TC9.6×10−5TD10.2×10−5T
The two long, straight wires carrying electric currents in opposite directions. The separation between the wires is 5.0 cm. Find the magnetic field at a point P midway between the wires.
View SolutionTwo perpendicular infinite wires are carrying current i as shown in the figure. The magnetic field at point P is :
_2019_CBT2_E01_008_Q01.png)
View SolutionTwo long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
View SolutionIn Fig. two long parallel wires (seen end-on) that are a distance R apart carry equal currents i in the same sense. Find the magnitude of the magnetic field at point P , which lies quidistant from the two wires at an angle θ from the plane of the wires.

View SolutionA semicircular wire of radius 5.0 cm carries a current of 5.0 A. A magnetic field B of magnitude 0.50 T exists along the perpendicular to the plane of the wire. Find the magnitude of the magnetic force acting on the wire.
View SolutionIn fig. two long parallel wires carry equal currents in opposite directions. Point O is situated midway between the wires and X−Y plane contains the two wires and the position Z-axis comes normally out of the plane of paper. The magnetic field B at O is non-zero along
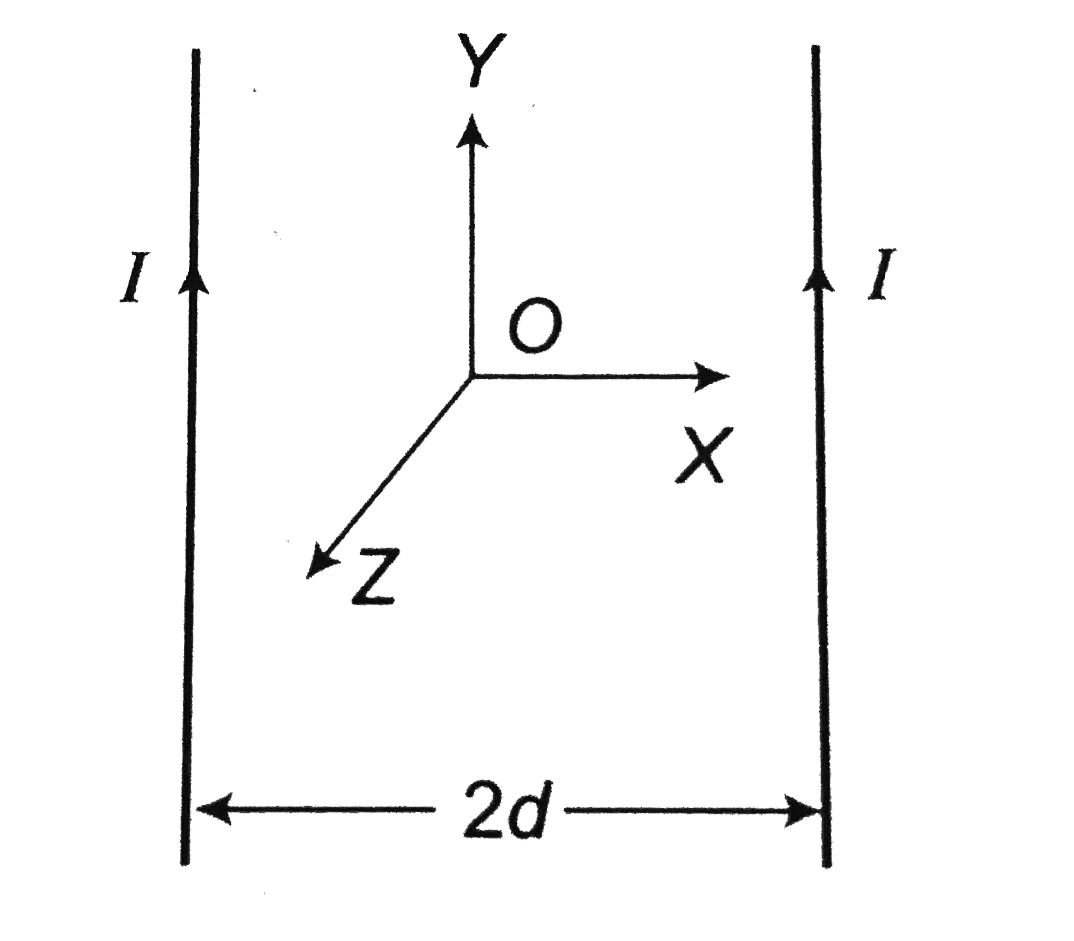
View SolutionThree long straight and parallel wires carrying currents are arranged as shown in the figure. The wire C which carreis a current of 5.0amp is so placed that it experiences no force. The distance of wire C from D is then
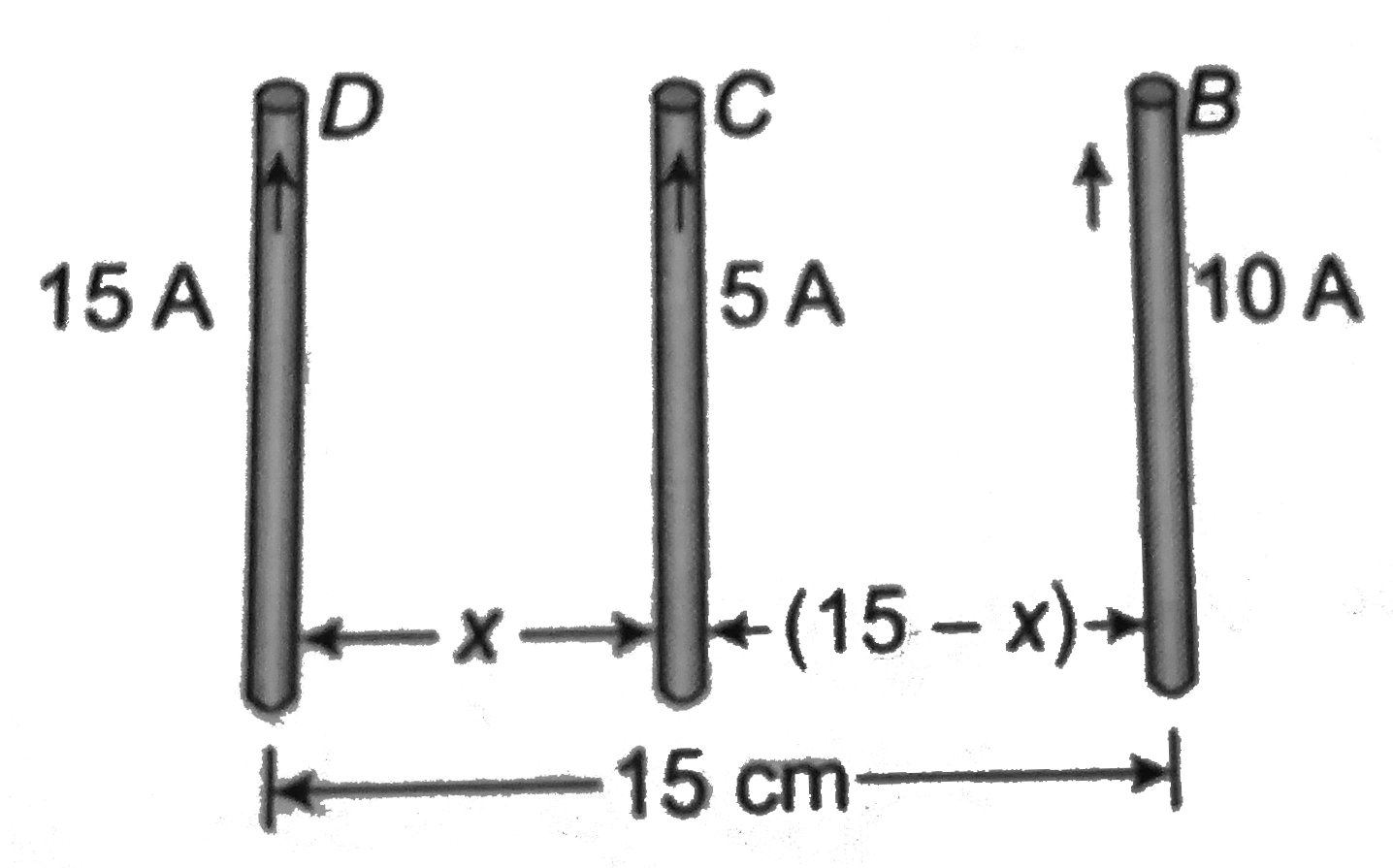
View Solution
