
Two waves of light in air, of wavelength λ=600.0nm, are initially in phase. They then both travel through a layer of plastic as shown in Figure, with L1=4.00μm,L2=3.50μm,n1=1.42, and n2=1.60. (a) What multiple of λ gives their phase difference after they both have emerged from the layers? (b) If the waves later arrive at some common point with the same amplitude, is their interference fully constructive, fully destructive, interme- diate but closer to fully constructive, or intermediate but closer to fully destructive?
(a) 0.700, (b) intermediate closer to fully destructive
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)66videos
INTERFERENCE AND DIFFRACTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)23videos
INTERFERENCE AND DIFFRACTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - CHECKPOINT6videos
INTERFERENCE AND DIFFRACTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - HYDROGEN ATOMEXERCISE - PRACTICE QUESTIONS(Integer Type)6videos
HYDROGEN ATOM
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Integer Type)4videos
MAGNETIC FIELDS DUE TO CURRENTS
Similar Questions
Assume that two waves of light in air, of wavelength 585 nm, are initially in phase. One travels through a glass layer of index of refraction n1=160 and thickness L. The other travels through an equally thick plastic layer of index of refraction n2=1.50. (a) What is the smallest value L should have if the waves are to end up with a phase difference of 5.65 rad? (b) If the waves arrive at some common point with the same amplitude, is their interference fully constructive, fully destructive, intermediate but closer to fully constructive, or intermediate but closer to fully destructive?
View SolutionTwo waves of light in air have the same wavelength and are intially in phase. They then travel through plastic layers with thickness of L1=3.5mm and L2=5.0mm and indices of refraction n1=1.7 and n2=1.25 as shown in figure. The rays later arrive at a common point. The longest wavelength of light for which constructive interference occurs at the point is
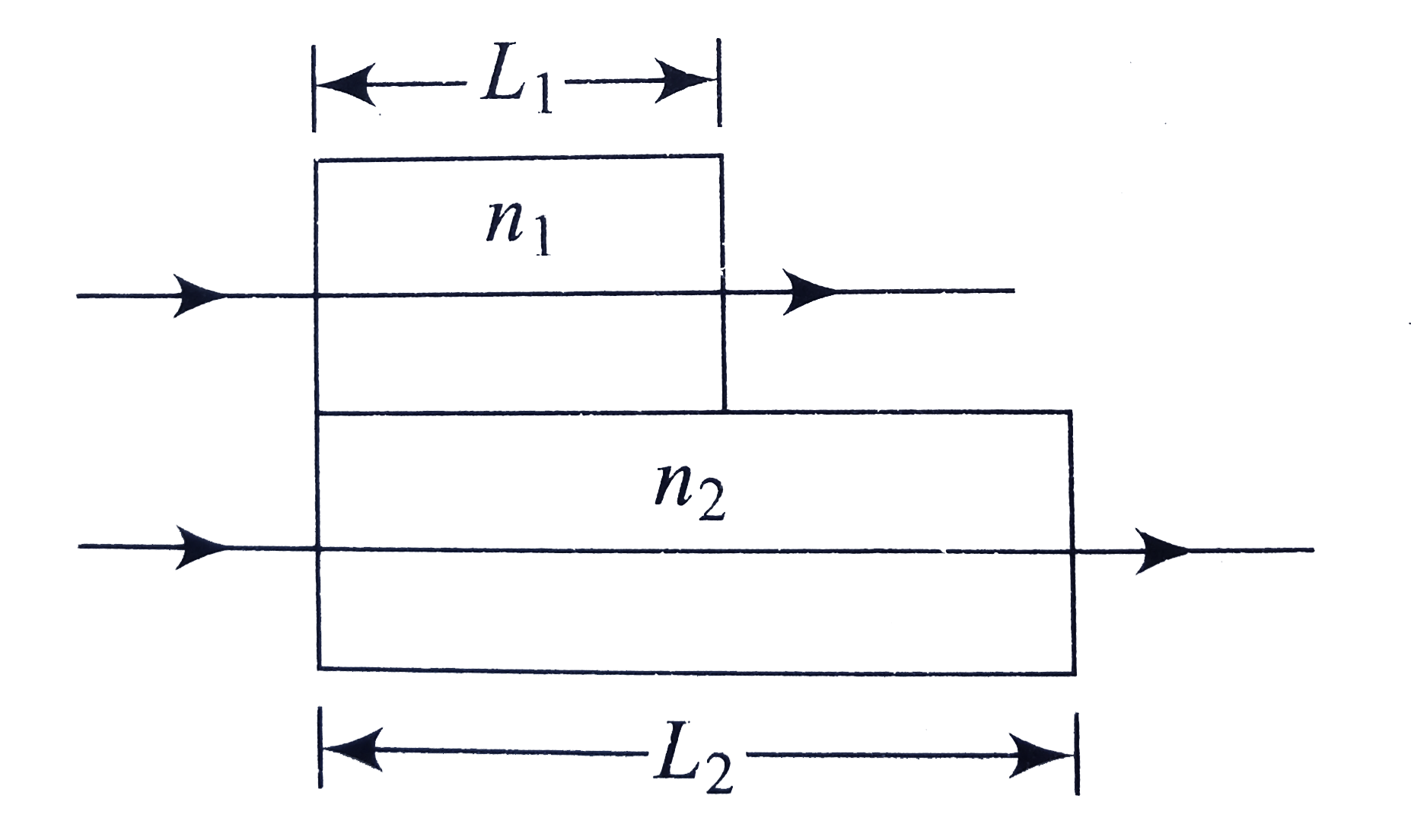 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two waves of light in air have the same wavelength and are intially in phase. They then travel through plastic layers with thickness of L1=3.5mm and L2=5.0mm and indices of refraction n1=1.7 and n2=1.25 as shown in figure. The rays later arrive at a common point. The longest wavelength of light for which constructive interference occurs at the point is
 A0.8μmB1.2μmC1.7μmD2.9μm
A0.8μmB1.2μmC1.7μmD2.9μm - Question 2 - Select One
If the phase difference between the two light waves arriving at a point is (2n-1) π radians. The condition for the minimumintensity of light at that point will be
AImin=(a1−a2)2BImin=a1−a2CImin=(a1+a2)2DImin=a21−a22
In Figure, a light ray is incident at angle θ1=55∘ on a series of five transparent layers with parallel boundaries. For layers 1 and 3. L1=20μm,L3=25μm,n1=1.6, and n3=1.15. (a) At what angle does the light emerge back into air at the riglit? (b) How much time does the light take to travel through layer 3?
 View Solution
View SolutionSuppose that the two waves have wavelength λ=610nm in air. What multiple of λ gives their phase difference when they emerge if (a) n1=1.50,n2=1.60, and L = 700 um, (b) n1=1.62,n2=1.72, and L = 700 um, and (c) n1=1.83,n2=1.59, and L = 2.16 um? (d) Suppose that in each of these three situations the waves arrive at a common point (with the same amplitude) after emerging, Rank the situations according to the brightness the waves produce at the common point.
View SolutionFind the speed of light of wavelength λ=780nm (in air) in a medium of refractive index μ=1.55.
(b) What is the wavelength of this light in the given medium ?View SolutionFind the speed of light of wavelength λ=780nm (in air) in a medium of refractive index μ=1.55.
(b) What is the wavelength of this light in the given medium ?View SolutionTwo light rays initially in same phase travel through two media of equal length L having refraction index μ1andμ2(μ1>μ2) as shown in figure. If the wavelength of light rays in air is λ, the phase difference of the emerging rays is given by
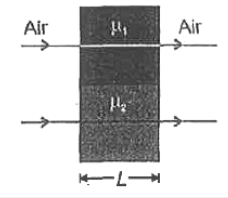 View Solution
View SolutionAssume that the two light waves, of wavelength 515 nm in air, are initially out of phase by π rad. The indexes of refraction of the media are n1=1.45 and n2=1.75. What are the (a) smallest and (b) second smallest value of L that will put the waves exactly in phase once they pass through the two media?
View Solution

