Using Biot Savart's law, derive the expression for the magnetic field at a point on the axis of a circular current loop.
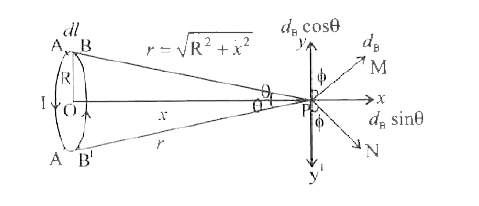
Consider a circular loop of radius R carrying a current I. Let P be a point at a distance x from the centre the , of the loop on axis. AB is current element of length dl. The distance of the point P from current element is r.
∴ From figure
r=√R2+x2sinθ=Rr
According to Biot-Savart.s law, magnetic field at the pont P due to the current element AB is
dB=μ04πIdlr2sinϕ
Since ϕ=90∘
dB=μ04πIdlr2 sin 90∘ ( ∵ sin 90∘=1)
dB=μ04πIdlr2 along PM
dB due to the current element A.B. at the point P is dB=μ04πIdlr2 along PN.
The magnetic field dB along PM can be resolved into two rectangular components dB cos ϕ along Py and dB sin ϕ along Px. Similarly the magnetic field dB along PN can be resolved into two components .
If we consider more small elements cos θ components cancel each other out .
ΣdBcosϕ=0 αΣdBcosθ#0
B=∫dBsinϕ
B=∫μ04πIdlr2sinϕ
Substituting the values of r=√R2+x2 and sin ϕ=Rr in the equation , we get
B=∫μ04πIdlR2+x2Rr=∫μ04πIdlR2+x2R√R2+x2=μ04πIR(R2+x2)3/2∫dl
But ∫dl=2πR→ circumference of the loop
∴B=μ0IR4π(x2+R2)3/2×2πR
∴B=μ04π2πIR2(x2+R2)3/2
Topper's Solved these Questions
Similar Questions
(a) Using Biot-Savart's law, derive the expression for the magnetic field in the vector form at a point on the axis of a circular current loop.
(b) What does a toroid consist of? Find out the expression for the magnetic field inside a toroid for N turns of the coil having the average radius r and carrying a current I. Show the magnetic field in the open space inside and exterior to the toroid is Zero.
View SolutionUsing Biot-Savart’s law, derive an expression for magnetic field at any point on axial line of a current carrying circular loop. Hence, find magnitude of magnetic field intensity at the centre of circular coil.
View SolutionUsing Biot-Savart’s law, derive an expression for magnetic field at any point on axial line of a current carrying circular loop. Hence, find magnitude of magnetic field intensity at the centre of circular coil.
View SolutionUsing Biot - Savart's law, derive an expression for magnetic field at any point on axial line of a current carrying circular loop. Hence, find magnitude of magnetic field intensity at the centre of circular coil.
View SolutionUse Biot-Savart law to derive the expression for the magnetic field on the axis of a current carrying circular loop of radius R.
Draw the magnetic field lines due to circular wire carrying current I.
View SolutionUse Biot-Savart law to derive the expression for the magnetic field on the axis of a current carrying circular loop of radius R.
Draw the magnetic field lines due to circular wire carrying current I.
View Solution(a) State Biot - Savart law and ecpress it in the vector form.
(b) Using Biot - Savart law, law obtain the expression for the magnetic field due to a circular coil of radius r, carrying a current I at point on its axis distant x from the centre of the coil.
View SolutionState Biot-Savart law, giving the mathematical expression for it.
Use this law to derive the expression for the magnetic field due to a circular coil carrying current at a point along its axis.
How does a circular loop carrying curent behave as a magnet?
View SolutionBiot Savart's law deals with the magnetic field induction at a point due to a………………. .
View SolutionState the Biot-Savart law. Use it to obtain an expression for magnetic field at the centre of a current carrying circular loop.
View Solution
