Using Eq.(6.2e), find the probability D of a particle of mass m and energy E tunneling through the potential barrier shown in fig. where U(x)=U0(1−x2/l2).
The potential is U(x)=U0(1−x2l2). The turning points are
EU0=1−x2l2orx=±l√1−EU0
Then D≈exp[−4ħ∫l√1−(E/U0)0√2m{U0)(1−x2l2)−E}dx]
=exp=exp[−4ħ∫l√1−(E/U0)0√2mU0√1−EU0−x2l2dx
=exp[−4lħ√2mV0∫x00√x20−x2dx],x0=√1−E/V0
The intergal is ∫x00√x20−x2dx=x20∫x/20cos2θdθ=π4x20
Thus D≈exp[−πlħ√2mU0(1−EU0)]
=exp[−πlħ√2mU0(U0−E)]
Topper's Solved these Questions
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Properties Of Atom
69 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Molecules And Crystals
48 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Elementary Particles
20 Videos
- DIRECT CURRENTBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - DIRECT CURRENTEXERCISE - All Questions
15 Videos
Similar Questions
Employing Eq.(6.2e), find the probability D of an electron with energy E tunneling through a potential barrier of width l and height U0 provided the barrier is shaped as shown:
(a) In fig 6.4
(b) in figure 6.5.

View SolutionMaking use of the solution of the foregoing problem, determine the probability of the particle with energy E=U0/2 to be located in the region x>l, if l2U0=(34π)2ħ2m.
View Solution
Knowledge Check
A particle with total energy E moves in one dimemsional region where the potential energy is U(x) The speed of the particle is zero where
AU(x)=0BU(x)=ECdU(x)dx=0Dd2U(x)dx2=0The potential energy of a particle of mass 'm' situated in a unidimensional potential field varies as U(x)=U0[1−cos(ax2)], where U0 and a are positive constant. The time period of small oscillations of the particle about the mean position-
Aπ√ma2U0B2π√2ma2U0C2π√ma2U0D4π√ma2U0The potential energy of a particle of mass m is given by U=12kx2 for x<0andU=0 for x≥0. If total mechanical energy of the particle is E, is speed at x=√2Ek is
AZeroB√2EmC√EmD√E2m
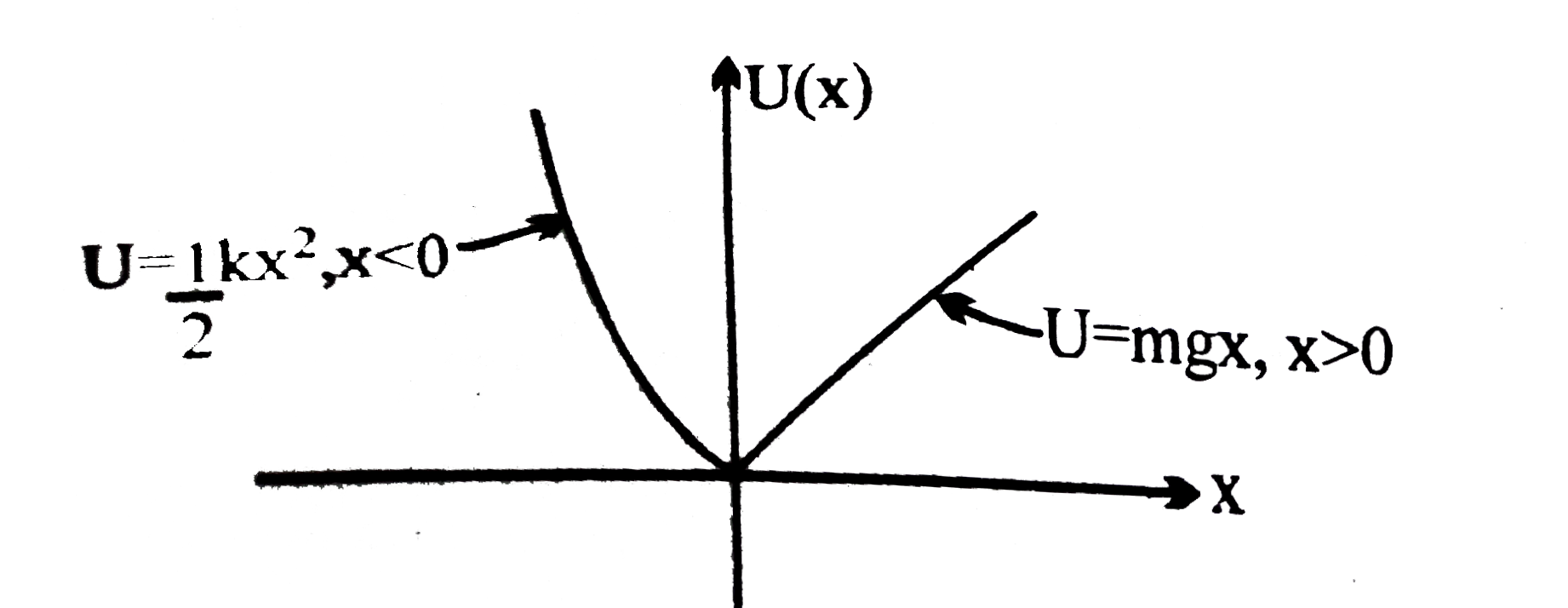
Apaticle of mass m moves in the potential energy U shown above. Find the period of the motion when the particle has total energy E.
View SolutionThe potential energy of a particle of mass 'm' situated in a unidimensional potential field varies as U(x)=U0[1−cos(ax2)], where U0 and a are positive constant. The time period of small oscillations of the particle about the mean position-
View SolutionThe potential energy of a particle of mass m is given by U(x)=U0(1−coscx) where U0 and c are constants. Find the time period of small oscillations of the particle.
View SolutionA particle of mass m is located in a unidimensional potential field U(x) whose shape is shown in fig. where U(0)=∞. Find

(a) the equation defining the possible values of enrgy of the particle in the region E<U0, reduce taht equation to the from
sinkl=±kl√ħ2/2ml2U0,
where k=√2mE/ħ. Solving this equation by graphical means, domonstrate that hte possible values of energy of the particle from a discontinuous spectrum,
(b)the minium value of the quantity l2U0 at which the first energy level appears in the region E<U0. At what minimum value of l2U0 does the nth level appear?
View SolutionA single conservative f(x) acts on a m=1kg particle moving along the x-axis. The potential energy U(x) is given by :
U(x)=20+(x−2)2
where x is in metres. At x=5m, a particle has kintetic energy of 20 J
The maximum value of potential energy is:
View Solution
