Velocity of a particle moving in a straight line varies with its displacement as v=(√4+4s)m/s. Displacement of particle at time t=0 is s=0. Find displacement of particle at time t=2s.
To solve the problem, we need to find the displacement of a particle at time t=2 seconds, given that its velocity varies with displacement as v=√4+4s m/s and that the initial displacement at t=0 is s=0.
1. Square the Velocity Equation:
v=√4+4s
Squaring both sides gives:
v2=4+4s
2. Identify Initial Conditions:
At t=0, the displacement s=0. Thus, we can find the initial velocity v when s=0:
v2=4+4(0)=4⟹v=√4=2m/s
So, the initial velocity u=2m/s.
3. Determine Acceleration:
From the equation v2=u2+2as, we can compare:
v2=4+4sandu2=4
This implies:
2a=4⟹a=2m/s2
4. Use the Kinematic Equation:
We can now use the kinematic equation to find the displacement s at t=2 seconds:
s=ut+12at2
Substituting the known values:
u=2m/s,t=2s,a=2m/s2
s=(2)(2)+12(2)(22)
s=4+12(2)(4)=4+4=8m
5. Final Answer:
The displacement of the particle at t=2 seconds is:
s=8meters
v=√4+4s
Squaring both sides gives:
v2=4+4s
At t=0, the displacement s=0. Thus, we can find the initial velocity v when s=0:
v2=4+4(0)=4⟹v=√4=2m/s
So, the initial velocity u=2m/s.
From the equation v2=u2+2as, we can compare:
v2=4+4sandu2=4
This implies:
2a=4⟹a=2m/s2
We can now use the kinematic equation to find the displacement s at t=2 seconds:
s=ut+12at2
Substituting the known values:
u=2m/s,t=2s,a=2m/s2
s=(2)(2)+12(2)(22)
s=4+12(2)(4)=4+4=8m
The displacement of the particle at t=2 seconds is:
s=8meters
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Exercise 6.1
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Exercise 6.2
3 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Example Type 7
1 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
Velocity-time graph of a particle moving in a straight line is shown in figure. At time t=0, displacement of the particle from mean position is 10 m. Find
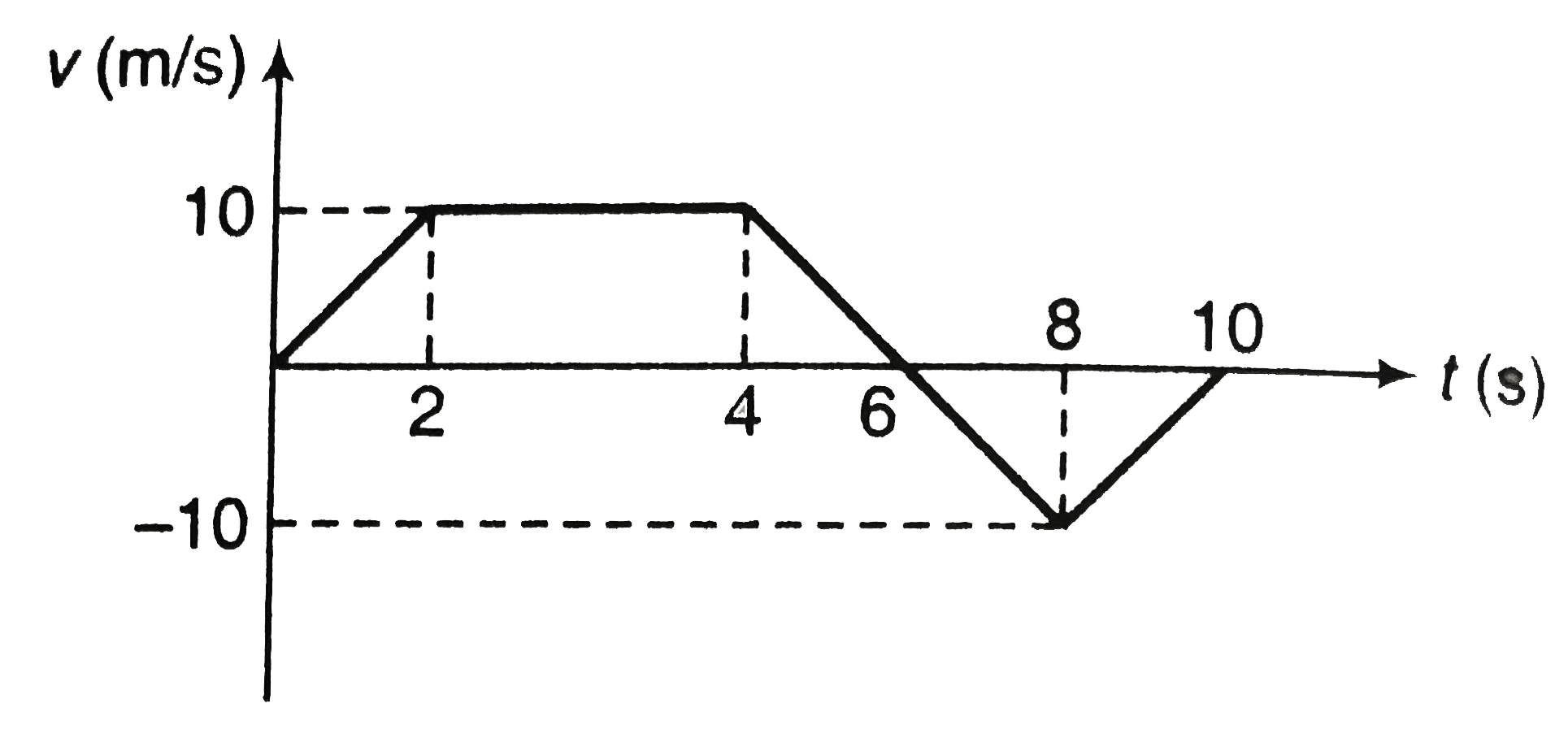
(a) acceleration of particle at t=1s,3sand9s.
(b) position of particle from mean position at t=10s.
(c) write down s-t equation for time interval (i)0≤t≤2s, (ii) 4s≤t≤8s
View SolutionVelocity-time graph of a particle moving in a straight line is shown in figure. Plot the corresponding displacement-time graph of the particle if at time t=0, displacement s=0.
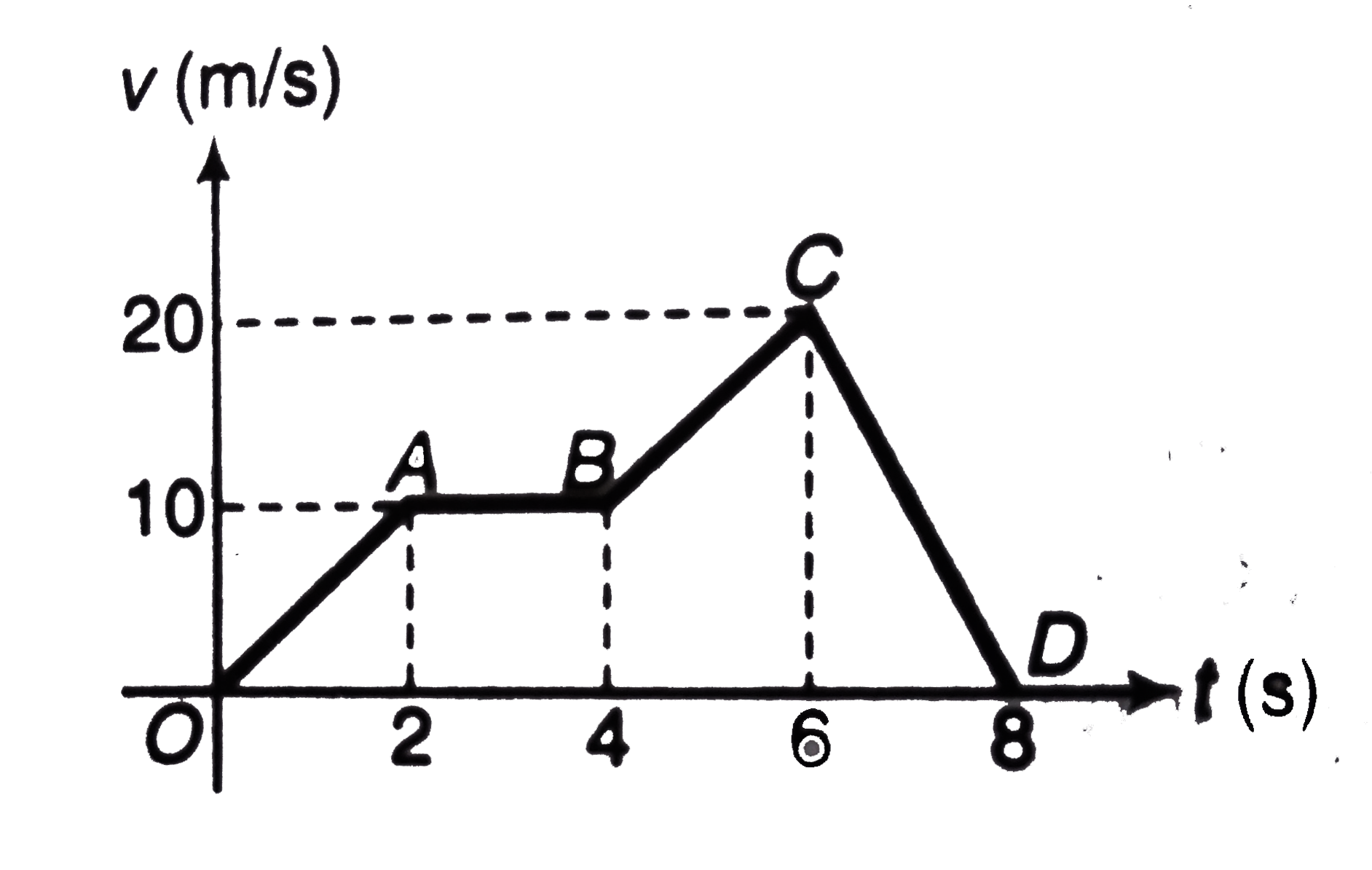
View SolutionVelocity-time graph of a particle moving in a straight line is shown in figure. Plot the corresponding displacement-time graph of the particle if at time t=0, displacement s=0.

View SolutionThe acceleration of a particle moving in a straight line varies with its displacement as,a=2s+1 veocity o particle is zero at zero displacement. Find the corresponding velocity - displacement equation.
View SolutionThe acceleration (a) of a particle moving in a straight line varies with its displacement (s) as a=2s. The velocity of the particle is zero at zero displacement. Find the corresponding velocity-displacement equation.
View SolutionThe velocity-time graph of a particle moving in a staight line is shown in the . Find the displacement and the distance trav elled by the particle in 6s.
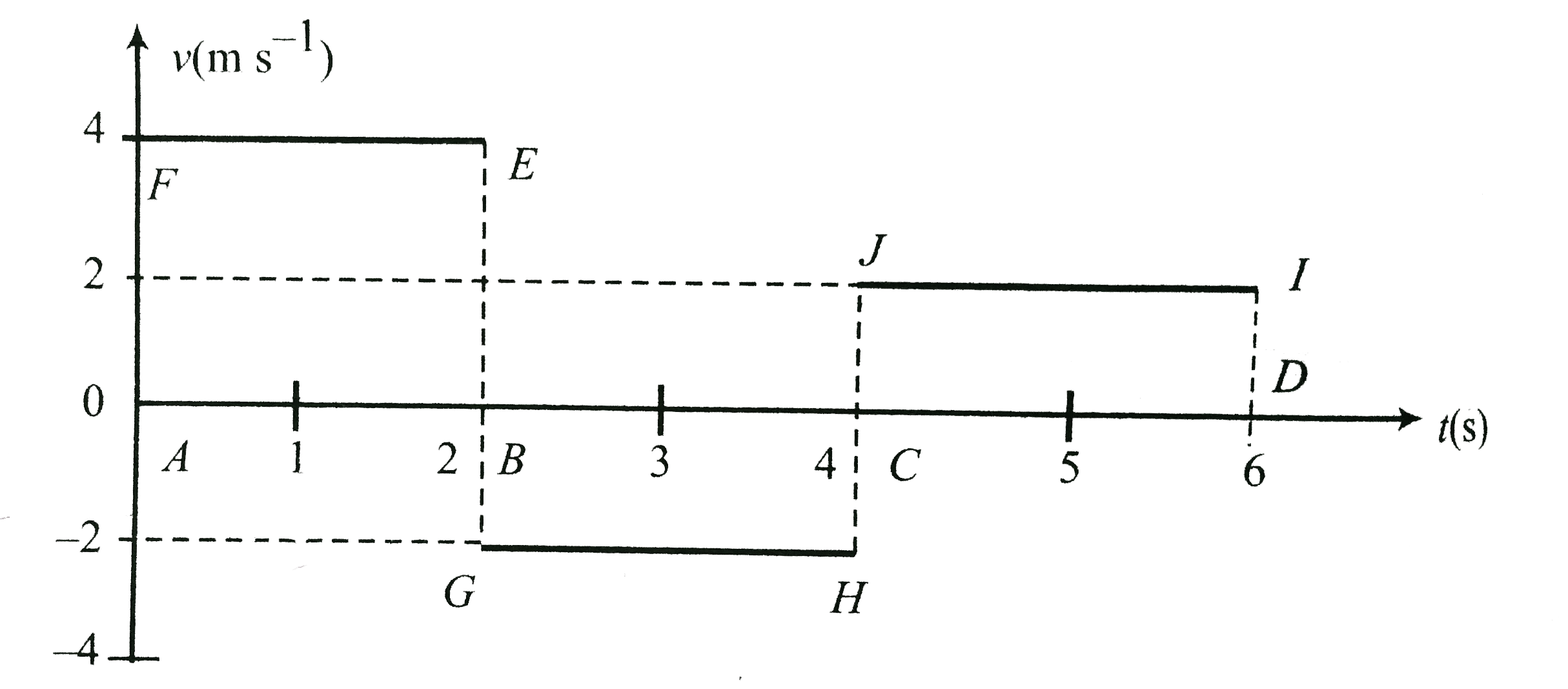 .
.
View SolutionVelocity-time equation of a particle moving in a straight line is, v=(10+2t+3t2) (SI units) Find
(a) displacement of particle from the mean position at time t=1s, if it is given that displacement is 20m at time t=0.
(b) acceleration-time equation.
View SolutionIf the velocity v of a particle moving along a straight line decreases linearly with its displacement from 20m/s to a value approaching zero at s=30m, determine the acceleration of the particle when s=15m.
View SolutionVelocity (in m/s) of a particle moving along x-axis varies with time as, v=(10+5t−t2) At time t=0,x=0. Find
(a) acceleration of particle at t=2s and
(b) x-coordinate of particle at t=3s
View SolutionIf the velocity v of particle moving along a straight line decreases linearly with its displacement s from 20ms−1 to a value approaching zero at s = 30 m, then acceleration of the particle at v=10ms^(-1) is
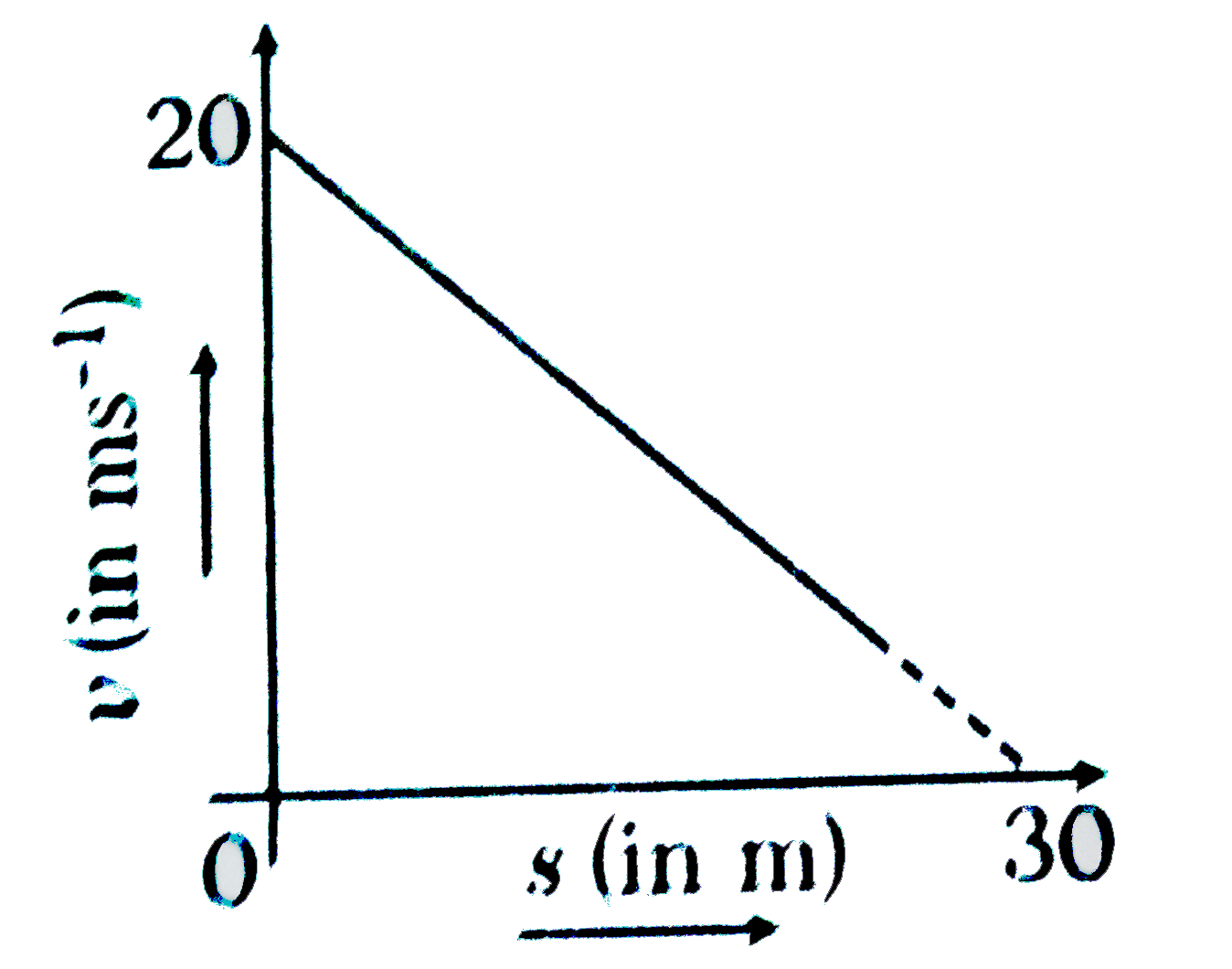
View Solution
