Water is filled in a container upto height 3m. A small hole of area 'a' is punched in the wall of the container at a height 52.5 cm from the bottom. The cross sectional area of the container is A. If a/A=0.1 then v2 is (where v is the velocity of water coming out of the hole)
50
51
48
51.5
The correct Answer is:A
To solve the problem, we will use Bernoulli's principle and the equation of continuity. Here are the steps to find v2, the square of the velocity of water coming out of the hole.
Step 1: Understand the given data
- Height of water in the container, H=3m=300cm
- Height of the hole from the bottom, h=52.5cm
- Area of the hole, a
- Cross-sectional area of the container, A
- Given ratio aA=0.1
Step 2: Calculate the effective height of water above the hole
The effective height h′ of water above the hole is calculated as:
h′=H−h=300cm−52.5cm=247.5cm=2.475m
Step 3: Apply Bernoulli's equation
According to Torricelli's law, the velocity v of efflux from the hole can be given by:
v=√2gh′
where g is the acceleration due to gravity, approximately 10m/s2.
Step 4: Substitute the values into the equation
Substituting g=10m/s2 and h′=2.475m:
v=√2⋅10⋅2.475
Step 5: Calculate v2
Calculating v2:
v2=2⋅10⋅2.475=49.5m2/s2
Step 6: Adjust for the area ratio
Since the area of the hole is much smaller than the cross-sectional area of the container, we need to consider the effect of the area ratio. The formula for the velocity considering the area ratio is:
v2=2gh′1−aA2
Substituting aA=0.1:
v2=49.5(1−0.1)2=49.5(0.9)2=49.50.81≈61.11m2/s2
Final Result
Thus, the square of the velocity of water coming out of the hole is approximately:
v2≈61.11m2/s2
- Height of water in the container, H=3m=300cm
- Height of the hole from the bottom, h=52.5cm
- Area of the hole, a
- Cross-sectional area of the container, A
- Given ratio aA=0.1
The effective height h′ of water above the hole is calculated as:
h′=H−h=300cm−52.5cm=247.5cm=2.475m
According to Torricelli's law, the velocity v of efflux from the hole can be given by:
v=√2gh′
where g is the acceleration due to gravity, approximately 10m/s2.
Substituting g=10m/s2 and h′=2.475m:
v=√2⋅10⋅2.475
Calculating v2:
v2=2⋅10⋅2.475=49.5m2/s2
Since the area of the hole is much smaller than the cross-sectional area of the container, we need to consider the effect of the area ratio. The formula for the velocity considering the area ratio is:
v2=2gh′1−aA2
Substituting aA=0.1:
v2=49.5(1−0.1)2=49.5(0.9)2=49.50.81≈61.11m2/s2
Thus, the square of the velocity of water coming out of the hole is approximately:
v2≈61.11m2/s2
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - AR_TYPE
1 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - MCQ_TYPE
3 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - True/False
1 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
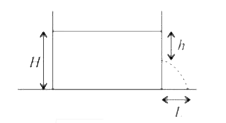
A liquid is filled in a container to a height H. A small hole is opened in the side of the container a height h below the surface of the liquid. The distance L from the bottom of the container of the point where the stream of liquid leaving the container meets the ground is :
View SolutionChoose the correct option:
Water is filled in a cylindrical container to a height of 3m. The ratio of the cross-sectional area of the orifice and the beaker is 0.1. The square of the speed of the liquid coming out from the orifice is (g=10m/s2).

View SolutionThe level of water in a tank is 5 m high . A hole of the area 10cm2 is made in the bottom of the tank . The rate of leakage of water from the hole is
View SolutionLiquid is filled in a container upto a height of H. A small hole is made at the bottom of the tank. Time taken to empty from H to H3 is t0. Find the time taken to empty tank from H3 to zero.
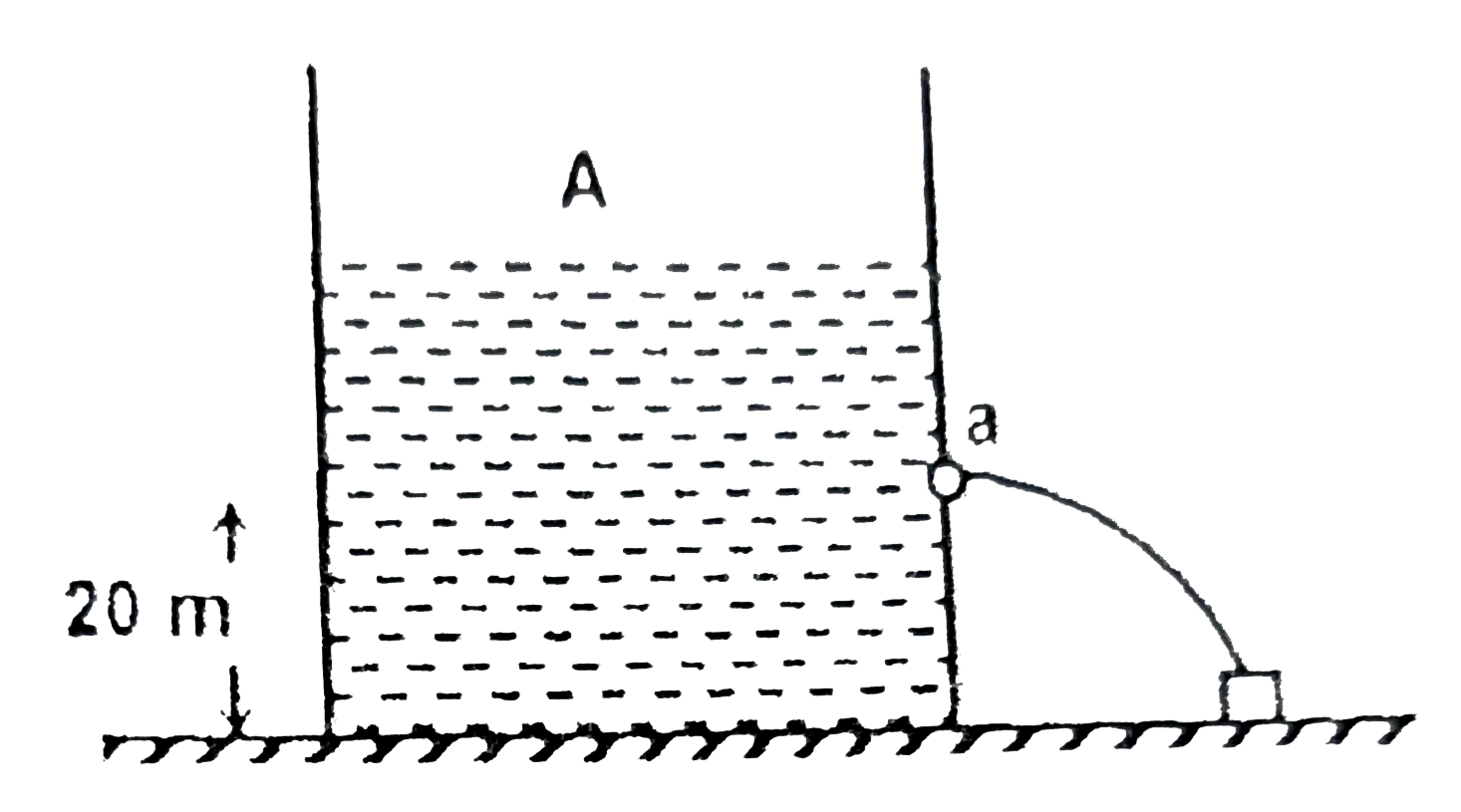
View SolutionWater is filled in a uniform container of area of cross section A. A hole of cross section area a (<<A) is made in the container at a height of 20m above the base. Water streams out and hits a small block on surface at some distance from container. Block is moved on surface in such a way that stream always hits the block. The initial velocity of the block (in m/s) is (Given aA=120). (Take g=10ms−2)
View SolutionA fixed container of height H with large cross-sectional area A is completely filled with water. Two small orifice of cross-sectional area a are made, one at the bottom and the other on the vertical side of the container at a distance H/2 from the top of the container find the time taken by the water level to reach a height of H/2 from the bottom of the container.
View SolutionThe flat bottom of cylinder tank is silvered and water (μ=43) is filled in the tank upto a height h. A small bird is hovering at a height 3h from the bottom of the tank. When a small hole is opened near the bottom of the tank, the water level falls at the rate of 1 cm/s. The bird will perceive that his velocity of image is 1/x cm/sec (in downward directions) where x is
View SolutionAn open vessel containing the liquid upto a height of 15 m. A small hole is made at height of 10 m from the base of the vessel then the initial velocity of efflux is (g = 10 m/s2)
View SolutionWater is filled in a container upto a height of 5cm. There is a concave mirror of radius of curvature 40cm. A person just above the surface observes image of 'A'. The distance of image from water surface is (μwater=1.33):
_2019_CBT7_E01_003_Q01.png)
View SolutionWater is filled to height h in a fixed vertical cylinder placed on horizontal surface. At time t=0 a small hole a drilled at a height h/4 from bottom of cylinder as shown. The cross section area of hole is a and the cross-section area of cylinder is A such that A>>a.

Let the value of horizontal distance of point where the4 water fall on horizontal surface from bottom of cylinder be x as shown. Then from time t=0 till water comes out of hole, pick the correct statement:
View Solution
