Water is filled up to a height h in a beaker of radius R as shown in the figure. The density of water is ρ, the surface tension of water is T and the atmospheric presure is p0. Consider a vertical section ABCDof the water on one side of this section by water on the other side of this section has magnitude

(a) ∣∣2p0Rh+πR2ρgh−2RT∣∣
(b)∣∣2p0Rh+Rρgh2=2RT∣∣
(c ) ∣∣p0(π)R2+Rρgh2−2RT∣∣
(d) ∣∣p0πR2+Rρgh2+2RT∣∣.
Force from right hand side liquid on left hand side liquid.
(i) Due to surface tension force=2RT(towards right)
(ii) Due to liquid pressure force =∫x=hx=0(p0+ρgx)(2R.dx)
=(2p0Rh+Rρgh2)(toward left)
∴ Net force is ∣∣2p0Rh+Rρgh2=2RT∣∣ (towards left)
∴ The correct option is (b)

Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Miscellaneous Examples10videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise16.16videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Medical entranes gallery49videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
Similar Questions
Water is filled up to a height h in a beaker of radius R as shown in the figure. The density of water is ρ, the surface tension of water is T and the atmospheric pressure is P0. Consider a vertical section ABCD of the water column through a diameter of the beaker. The force on water on one side of this section by water on the other side of this section has magnitude
 View Solution
View SolutionA small air bubble of radius 'r' is at a depth 'h' below the water surface (density of water=ρ). Surface tension of water is T, atmospheric pressure is p0. Find pressure inside the air bubble for the condition r<<h
View SolutionWill the height of the water column change if the cross section of the water column is made wider ?
View SolutionA container filled with a liquid of density 4p as shown in the figure. The velocity efflux through orifice is (ρ is density of water and g = 10 ms−2)
_PHY_E05_013_Q01.png) View Solution
View SolutionWater rises to a height h when a capillary of radius r is dipped in water. For another capillary of radius 2r dipped in water, it rises to the height
View SolutionWater is kept in a beaker of radius 5.0 cm. Consider a diameter of the beaker on the surface of the water. Find the force by which the surface on one side of the diameter pulls the surface on the other side. Surface tension of water =0.075Nm−1.
View SolutionThe mean density of sea water is ρ, and bulk modulus is B. The change in density of sea water in going from the surface of water to a depth of h is
View SolutionConsider a small water drop in air . If T is the surface tension , then what is the force due to surface tension acting on the smaller section ABC ?
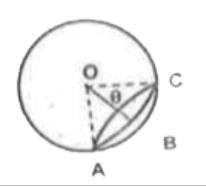 View Solution
View SolutionIn the figure shown the velocity and pressure of the liquid at the cross section (2) are given by (If P0 is the atmospheric pressure).
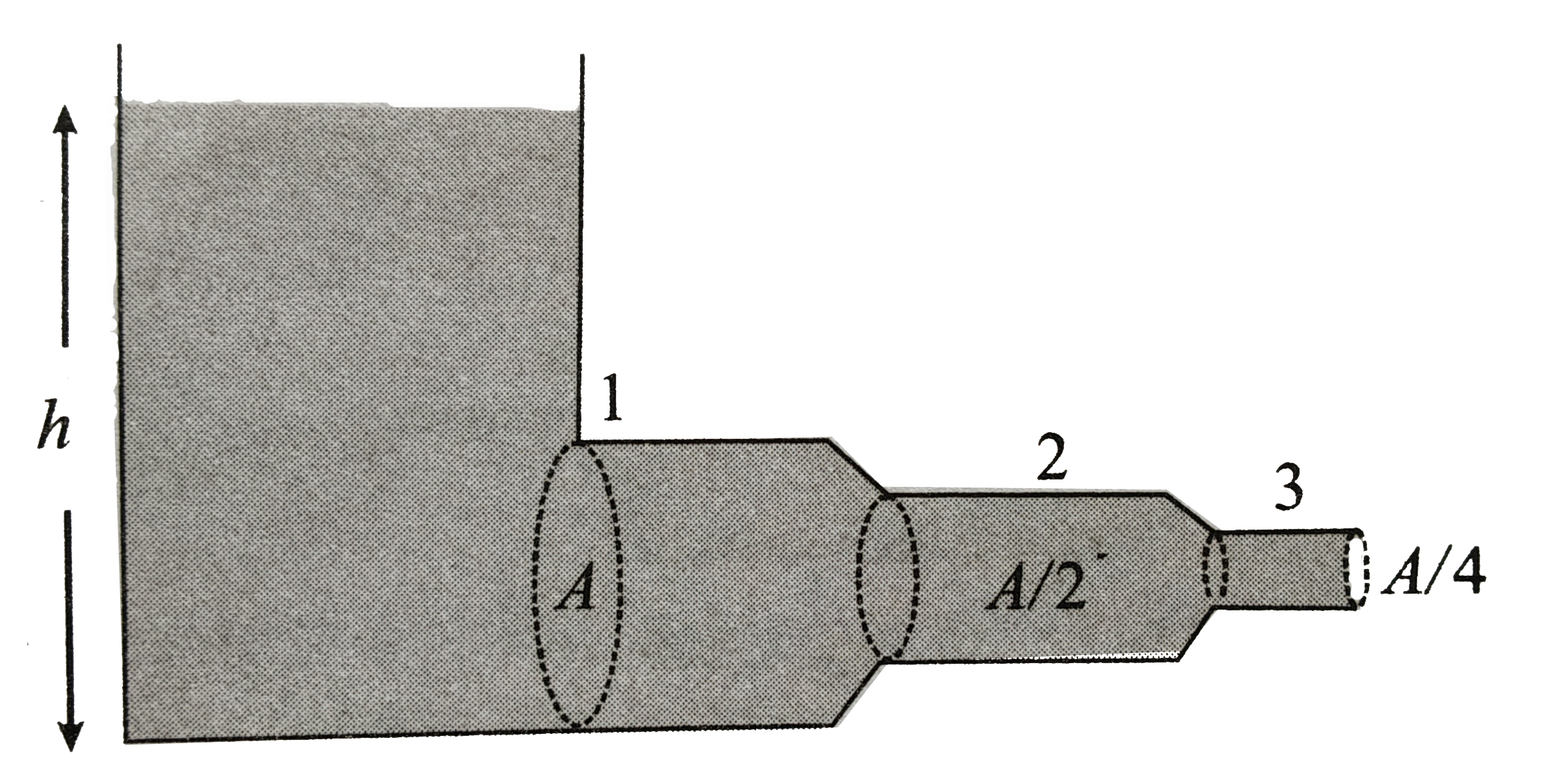 View Solution
View SolutionA liquid is kept in a beaker of radius 4 cm. Consider a diameter of the beaker on the surface of the water. Find the force by which the surface on one side of the diameter pulls the surface on the other side. Surface tension of liquid =0.075Nm−1
View Solution

