What does a toroid consist of ? Show that for an ideal toroid of closely wound turns, the magnetic field (i) inside the toroid is constant, and (ii) in the open space inside and exterior to the toroid is zero.
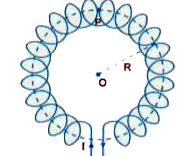
A toroid consists of an anchor ring of mean radius R, over which a large number of turns (say N) of an insulated metallic wire is wound.
(i) When a current I is passed through the toroid, the magnetic field produced will be same at all points on the central axis of the right (shown by dotted curve in the figure) and directed along tangent to the ring. Hence,
∮→B.→dl=∮Bdl=B∮dl=B(2πR)
and according to Ampere.s circuital law
∮→B.→dl=μ0 (total current enclosed) = μ0(NI)
∴ B.2πR=μ0NI
⇒ B=μ0NI2πR=μ0nI
Where n=N2πR = Number of turns per unit length of toroid.
Obviously this magnetic field is constnat at all point inside the toroid.
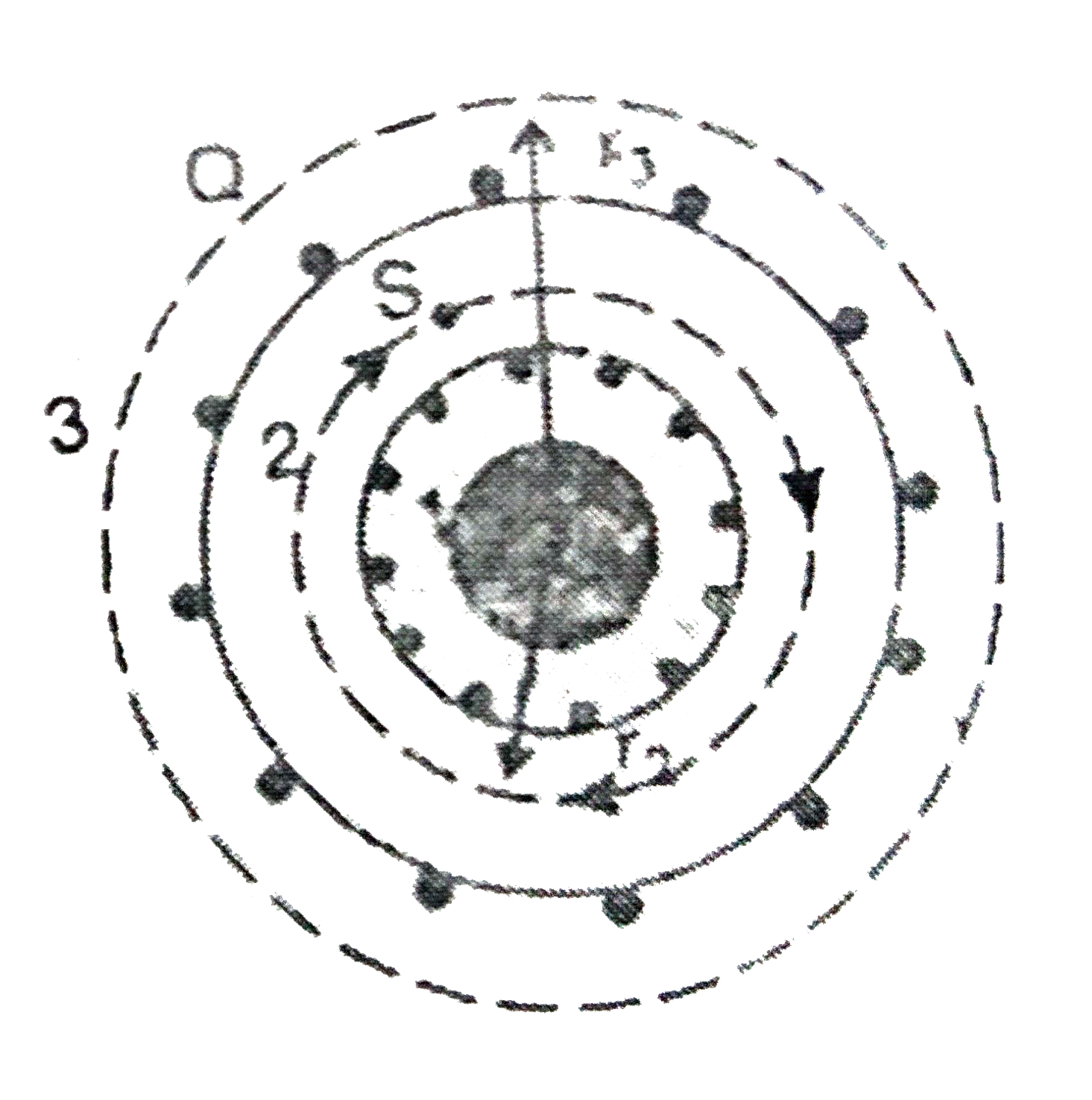
(ii) If we apply Ampere.s law to find magnetic field either in (a) open space inside the toroid , or (b) open space exterior to the toroid, then for any closed loop of radius .r. , we have
∮→B.→dl=B(2πr)=μ0(I)=μ0(0)
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - LONG ANSWER QUESTIONS-II
11 Videos
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - SELF ASSESSMENT TEST (SECTION A) (MULTIPLE CHOICE QUESTIONS)
5 Videos
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - SHORT ANSWER QUESTIONS
41 Videos
- MODEL TEST PAPER 3 (UNSOLVED)BOOK - U-LIKE SERIESCHAPTER - MODEL TEST PAPER 3 (UNSOLVED)EXERCISE - SECTION A
3 Videos
- NUCLEIBOOK - U-LIKE SERIESCHAPTER - NUCLEIEXERCISE - Self Assessment Test
10 Videos
Similar Questions
(a) How is a toroid different from a solenoid?
(b) Show that in an ideal toroid, the magnetic field (i) inside the toroid and (ii) outside the toroid at any point in the open space is zero.
View Solution(a) Using Biot-Savart's law, derive the expression for the magnetic field in the vector form at a point on the axis of a circular current loop.
(b) What does a toroid consist of? Find out the expression for the magnetic field inside a toroid for N turns of the coil having the average radius r and carrying a current I. Show the magnetic field in the open space inside and exterior to the toroid is Zero.
View Solution
Knowledge Check
Field inside a toroid is
Adirectly proportional to its lengthBdirectly proportional to currentCinversely proportional to total number of turnsDinversely proportional to currentA toroid having 200 turns carries a current of 1A. The average radius of the toroid is 10 cm. the magnetic field at any point in the open space inside the toroid is
A4×10−3TBzeroC0.5×10−3TD2×10−3TToroid has a core (non-ferromagnetic) of inner radius 25 cm and outer radius 26 cm, around which 3500 turns of a wire wound. If the current in the wire is 11A, what is the magnetic field (a) outside the toroid, (b) inside the core of the toroid, and (c) in the empty space surrounded by the torroid.
A(0,0,3×10−2T)B(0,0,0)C(0,3×10−2T,0)D(3×10−2T,0,3×10−2T)
Magnetic Field Of A Toroid
View SolutionWhat is the shape of the coils for an ideal toroid?
View SolutionA toroid has a core (non-ferromagnetic) of inner radius 25 cm and outer radius 26 cm, around which 3500 turns of a wire are found. If the current in the wire is 11 A, what is the magnetic field (i) outside the toroid, (ii) inside the core of the toroid, and (iii) in the empty space surrounded by the toroid.
View SolutionMagnetic field inside a long solenoid |Questions |Toroid
View SolutionA toroid having 200 turns carries a current of 1A. The average radius of the toroid is 10 cm. the magnetic field at any point in the open space inside the toroid is
View Solution
