Question

What is the period of oscillation of a liquid contained in a U - tube executing shm ?

Explanation

To find the period of oscillation of a liquid contained in a U-tube executing simple harmonic motion (SHM), we can follow these steps:

1. Understanding the Setup:
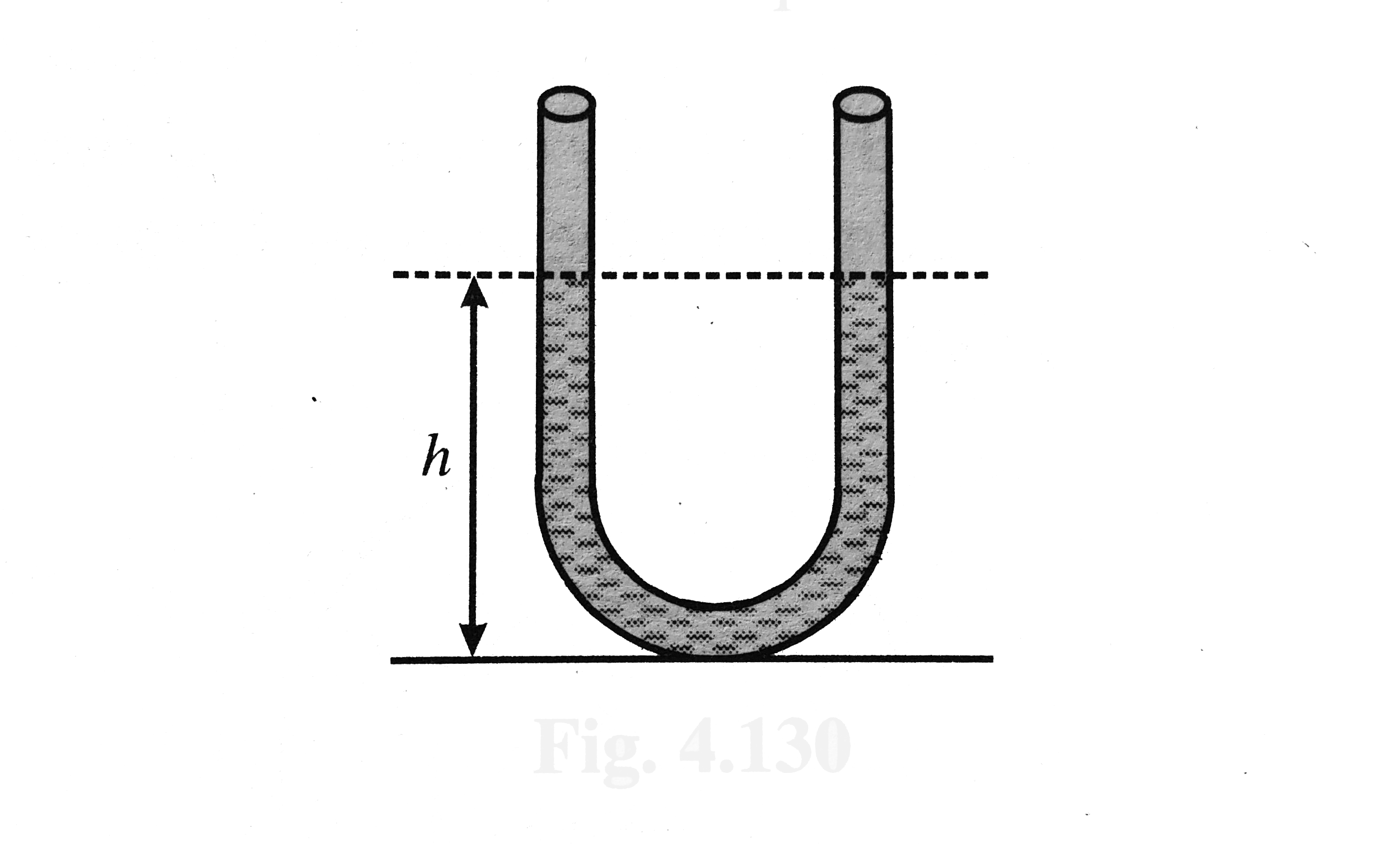
- We have a U-tube filled with liquid. When the liquid is displaced by a distance \( y \), the height of the liquid on one side decreases by \( y \) and increases by \( y \) on the other side.

2. Defining the Variables:
- Let \( A \) be the cross-sectional area of the U-tube.
- Let \( \rho \) be the density of the liquid.
- The total length of liquid on both sides of the U-tube is \( 2L \).

3. Calculating the Mass of the Liquid:
- The mass \( m \) of the liquid in the U-tube can be expressed as:
\( m = \rho \times \text{Volume} = \rho \times A \times 2L \)

4. Finding the Restoring Force:
- The restoring force \( F_R \) acting on the liquid due to the displacement \( y \) is equal to the weight of the liquid displaced. The volume of the displaced liquid on both sides is \( 2Ay \).
- Therefore, the restoring force can be calculated as:
\( F_R = \text{Weight of displaced liquid} = \rho \times (2Ay) \times g = 2\rho A g y \)
- Note that the restoring force acts in the opposite direction to the displacement, hence it is negative:
\( F_R = -2\rho A g y \)

5. Using the SHM Formula:
- In SHM, the restoring force is proportional to the displacement:
\( F = -k y \)
- Here, \( k \) (the spring constant equivalent for this system) can be identified as \( 2\rho A g \).

6. Calculating the Time Period:
- The time period \( T \) of SHM is given by:
\( T = 2\pi \sqrt{\frac{m}{k}} \)
- Substituting \( m \) and \( k \):
\( T = 2\pi \sqrt{\frac{\rho \cdot 2A \cdot L}{2\rho A g}} = 2\pi \sqrt{\frac{L}{g}} \)

7. Conclusion:
- The period of oscillation of the liquid in the U-tube is:
\( T = 2\pi \sqrt{\frac{L}{g}} \)
- This shows that the period is independent of the density of the liquid.