What is the tension in a rod of length length L and mass M at a distance y from when the rod is acted on by two unequal force and as shown in.
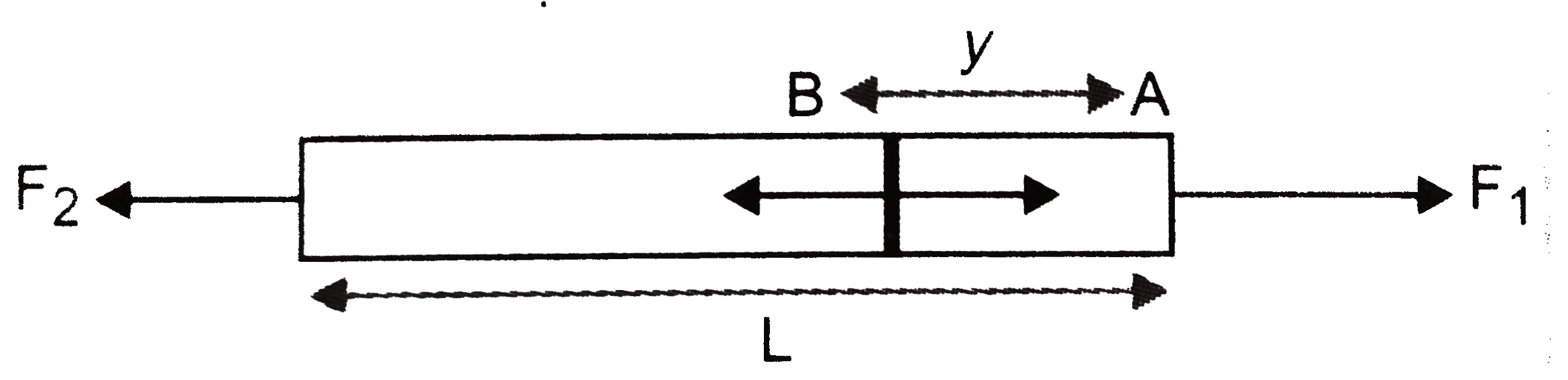
As net force on the rod and its mass is M. So, acceleration of the rod will be
…(i)
Now considering the motion of part AB of the rod [which has mass and acceleration a given by Eqn. (i)] assuming that tension at B is T,
Substituting a from Eqn (i)
or
To calculate tension at B we can also consider the motion of the other part of rod, i.e., BC. However, then equation of motion will be,
which of solving gives again,
Topper's Solved these Questions
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Problem for practice
30 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Objective Questions
134 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension
12 Videos
- BASIC MATHEMATICSBOOK - GRB PUBLICATIONCHAPTER - BASIC MATHEMATICSEXERCISE - Problems For Practice
35 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type
11 Videos
Similar Questions
Find the position of the centre of two unequal antiparallel forces. The distance between the points of application of the forces F1 and F2 is a.
View SolutionThe length of a metal wire is l1 when the tension in it is F1 and l2 when the tension becomes F2. Find the natural length of wire.
View Solution
Knowledge Check
A rod of length L and mass M is acted on by two unequal forces F1 and F2(<F)as shown in the figure.
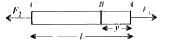
The tension in the rod at a distance y from the end A is given byAF1(1−yL)+F2(yL)BF2(1−yL)+F1(YL)C(F1−F2)yLDNone of theseTwo forces F1 and F2 are acting on a rod abc as shown in figure.
 Aif F1=F2 then τa=τb=τc ( for both forces)Bif F1=F2 then τa=τc≠τb ( for both forces)Cif F1≠F2 then τa≠τb≠τc ( for both forces)Dif F1≠F2 then τa=τc≠τb ( for both forces)
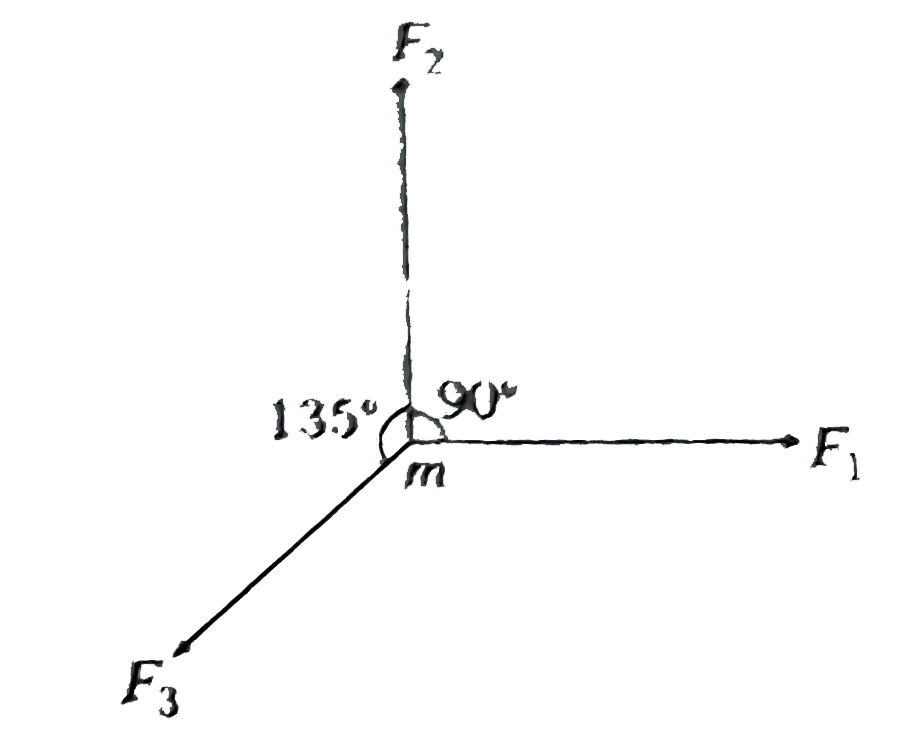
Aif F1=F2 then τa=τb=τc ( for both forces)Bif F1=F2 then τa=τc≠τb ( for both forces)Cif F1≠F2 then τa≠τb≠τc ( for both forces)Dif F1≠F2 then τa=τc≠τb ( for both forces)When a force F acts on a body of mass m, the acceleration produced in the body is a. If three equal forces F1=F2=F3=F act on the same body as shown in figure the acceleration produced is
 A(√2−1)aB(√2+1)C√2Da
A(√2−1)aB(√2+1)C√2Da
A mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to tke rod.

View SolutionA 100 N uniforms rod of length 6I is supported by two forces F1 and F2 as shown here. What is the ratio for F1 to F2?

View SolutionFor the system shown in fig, there is no friction anywhere. Masses m1andm2 can move up or down in the slots cut in mass M. Two non-zero horizontal force F1 and F2 are applied as shown. The pulleys are massles and frictionless. Given m1≠m2

Let F1 and F2 are applied in such a way that m1andm2 do not move w.r.t. M. then what is the magnitude of the acceleration of M? Let m1>m2.
View SolutionWhen a force F acs on a body of mass m the acceleration product in the body is a . If htree equal forces F1=F2=F3=F act on the same body as shown in figure the accleration produced is
View SolutionA uniform rope of mass (m) and length (L) placed on frictionless horizontal ground is being pulled by two forces FAandFB at its ends as shown in the figure. As a result, the rope accelerates toward the right.

Acceleration (A) of the rope is
View Solution
