When a jet of liquid strikes a fixed or moving surface, it exerts thru

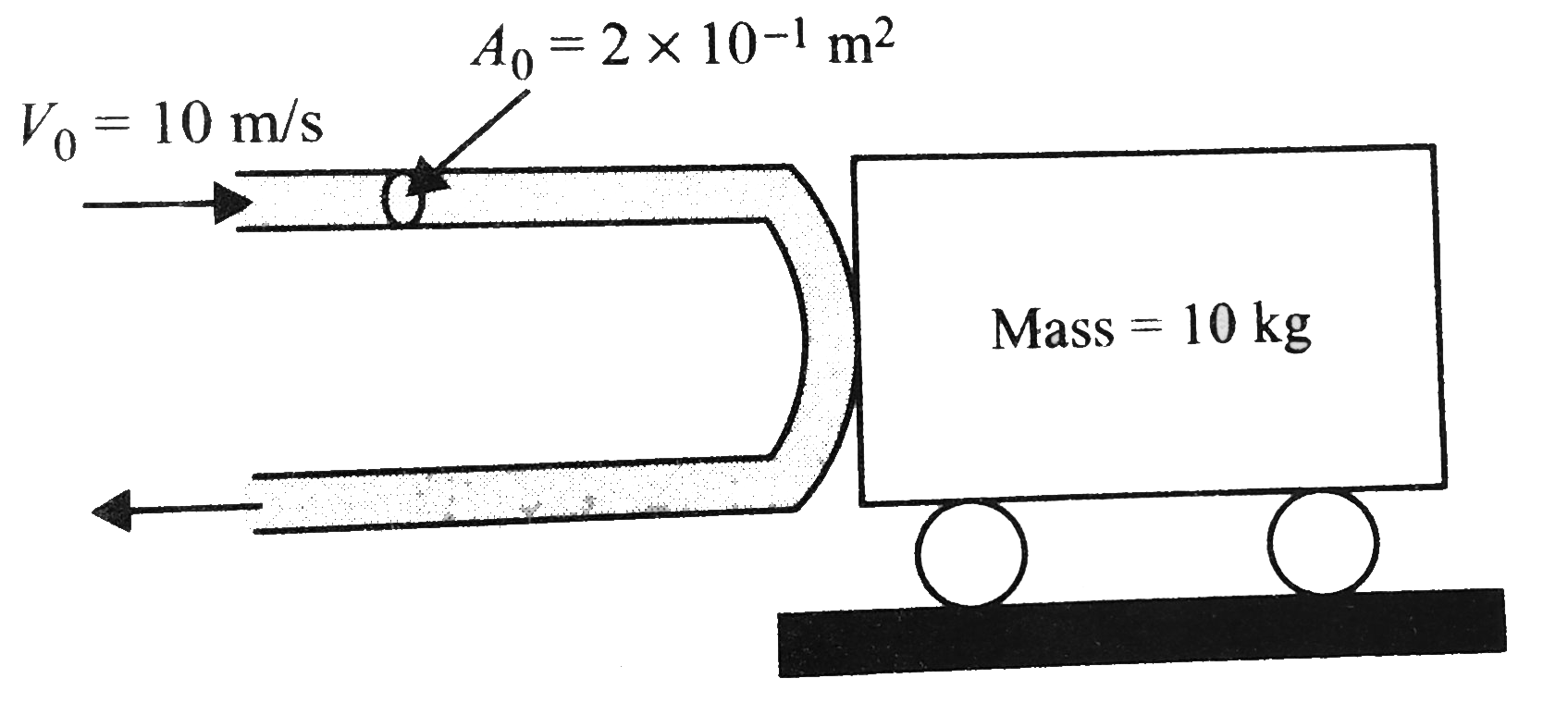
When a jet of liquid strikes a fixed or moving surface, it exerts thrust on it due to rate of change of momentum.
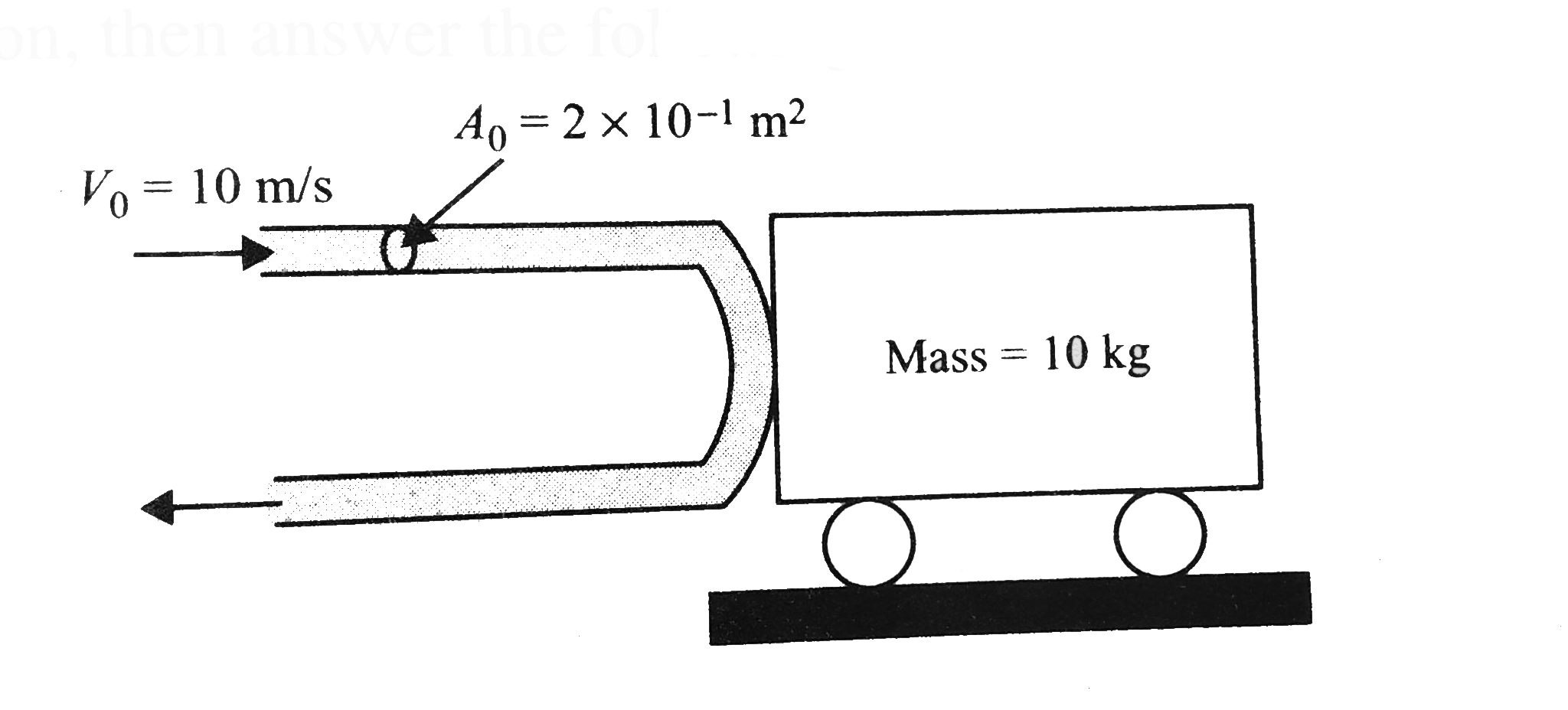
ocr_image
$F = (ρ A V_{0}) V_{0} - (ρ A V_{0}) V_{0} cos θ = ρ A V_{0}^{2} [1 - cos θ]$ If surface is free and starts moving due to thrust of the liquid, then at any instant, the above equation gets modified based on relative change of momentum with respect to surface. Let, at any instant, the velocity of surface be $u$ . Then the above equation becomes $< b r > F = ρ A {(V_{0} - u)}_{0}^{2} [1 - cos θ]$ Based on the above concept, as shown in the following figure, if the cart is frictionless and free to move in the horizontal direction, then answer the following.
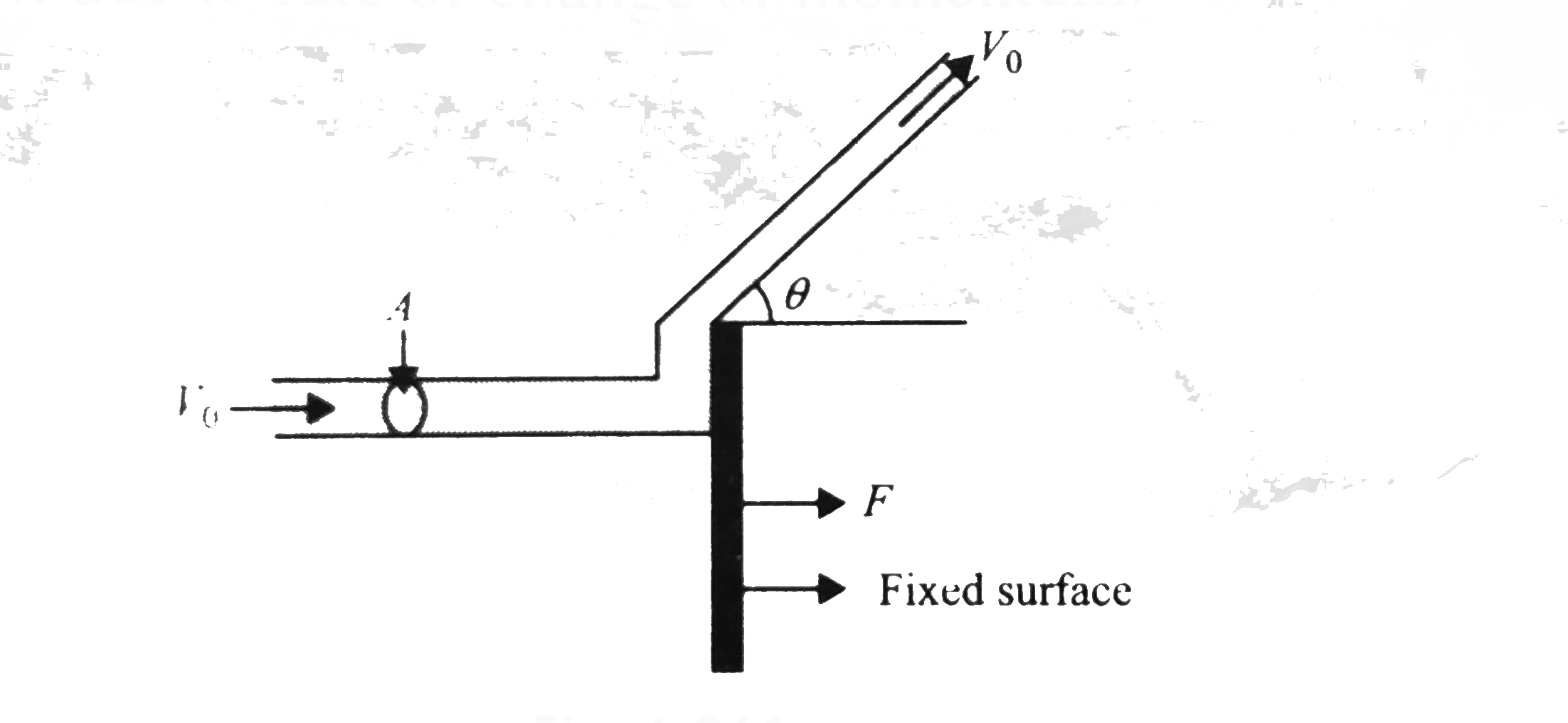
ocr_image
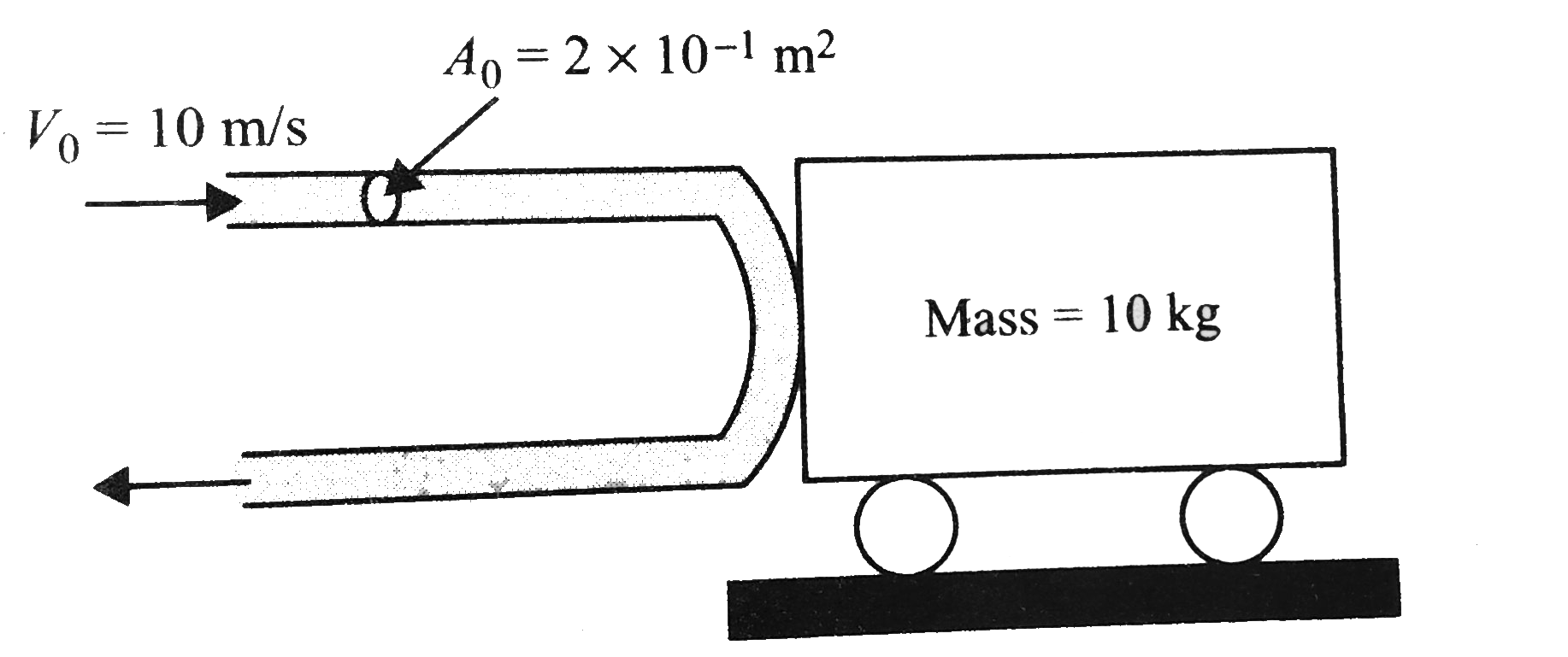
Given that cross sectional area of jet $= 2 \times 10^{- 4} m^{2}$ velocity of jet $V_{0} = 10 m / s$ density of liquid $= 1000 k g / m^{3}$ ,mass of cart $M = 10 k g$ .
The time at which velocity of cart becomes $2 \frac{m}{s}$ is equal to

View Solution

When a jet of liquid strikes a fixed or moving surface, it exerts thrust on it due to rate of change of momentum.
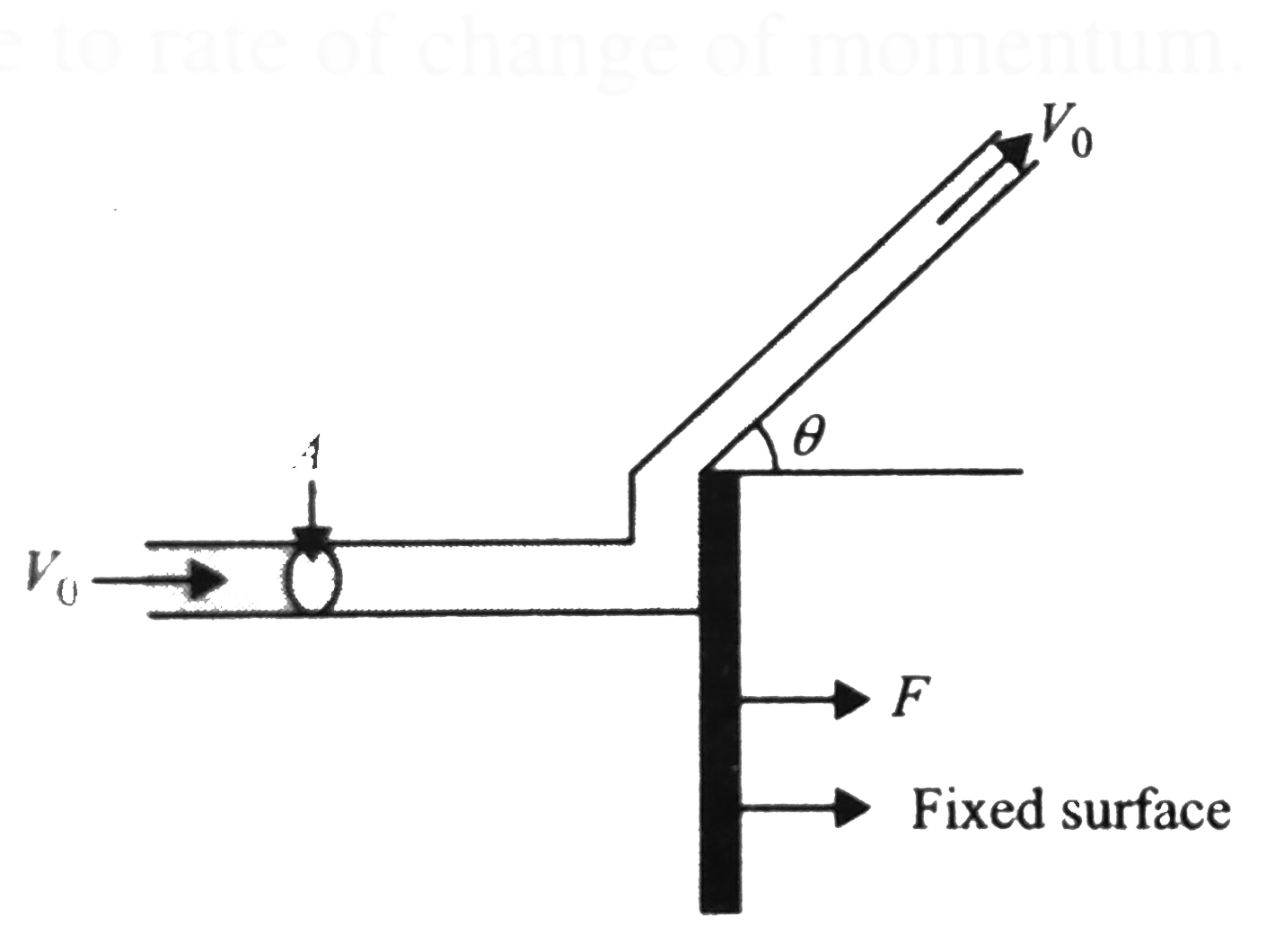
ocr_image
$F = (ρ A V_{0}) V_{0} - (ρ A V_{0}) V_{0} cos θ = ρ A V_{0}^{2} [1 - cos θ]$ If surface is free and starts moving due to thrust of the liquid, then at any instant, the above equation gets modified based on relative change of momentum with respect to surface. Let, at any instant, the velocity of surface be $u$ . Then the above equation becomes $< b r > F = ρ A {(V_{0} - u)}_{0}^{2} [1 - cos θ]$ Based on the above concept, as shown in the following figure, if the cart is frictionless and free to move in the horizontal direction, then answer the following.
ocr_image
Given that cross sectional area of jet $= 2 \times 10^{- 4} m^{2}$ velocity of jet $V_{0} = 10 m / s$ density of liquid $= 1000 k g / m^{3}$ ,mass of cart $M = 10 k g$ .
The power supplied to the cart when its velocity becomes $5 m / s$ is equal to

View Solution

A spherical rain drop evaporates at a rate proportional to its surface area at any instant $t .$ The differential equation giving the rate of change of the radius of the rain drop is _____

View Solution

A spherical rain drop evaporates at a rate proportional to its surface area at any instant $t .$ The differential equation giving the rate of change of the radius of the rain drop is _____

View Solution

A conducting rod AB of length l is projected on a frictionless frame PSRQ with velocity $v_{0}$ at any instant. The velocity of the rod after time t is

View Solution

Wedge of $10 k g$ is free to move on horizontal surface. At the given instant, acceleration of wedge is (string and pulleys are ideal)
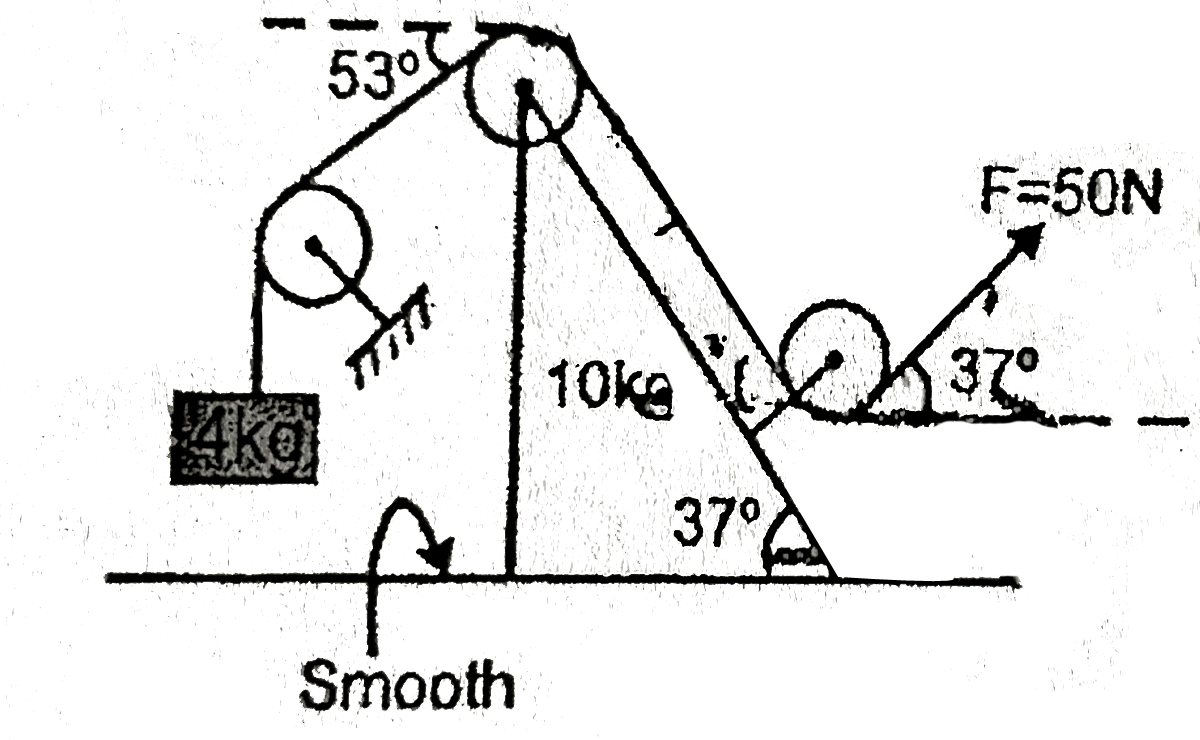ocr_image

View Solution

The volume of a spherical balloon is increasing at the rate of 20 $c m^{3}$ / $sec$ . Find the rate of change of its surface area at the instant when radius is 5 cm.

View Solution

A uniform cube of mass m and edge a moves on a horizontal surface along the positive x-axis, with initial velocity $v_{0}$ . Then

View Solution

The momentum of a particle of mass of m moving with a velocity v is p= mv. What is the rate of change of momentum ? Assume that m is constant .

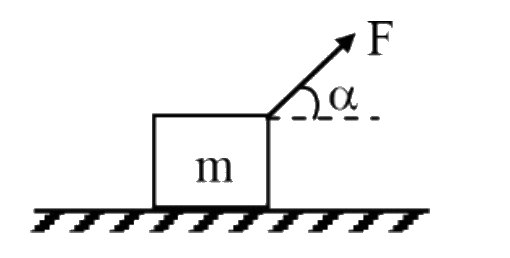
View Solution

At the instant $t = 0$ , a force $F = k t$ (k is a constant) acts on a small body of mass m resting on a smooth horizontal surface. The time, when the body leaves the surface is
ocr_image

View Solution

The correct Answer is:B

$F - ρ_{A} {(V_{0} - 0)}_{0}^{2} [1 - {cos 180}^{\circ}]$
$= 2 ρ A v^{2} = 2 \times 1000 \times 10^{- 4} \times 10 \times 10 = 40 N$

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-FLUID MECHANICS-Linked Comprehension

The correct Answer is:B

F−ρA(V0−0)2[1−cos180∘] =2ρAv2=2×1000×10−4×10×10=40N

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-FLUID MECHANICS-Linked Comprehension

$F - ρ_{A} {(V_{0} - 0)}_{0}^{2} [1 - {cos 180}^{\circ}]$
$= 2 ρ A v^{2} = 2 \times 1000 \times 10^{- 4} \times 10 \times 10 = 40 N$