If the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
What is the value of vertical acceleration of box for given horizontal acceleration (g/2), so that no part of the bottom of the box is exposed?
g/2 upwards
g/4 downwards
g/4 upwards
not possible
The correct Answer is:A
To solve the problem, we need to analyze the forces acting on the liquid inside the box when it is subjected to horizontal and vertical accelerations. The goal is to determine the vertical acceleration required to ensure that no part of the bottom of the box is exposed.
1. Understand the Setup:
- The box has a base of 6 m x 6 m and a height of 2 m.
- It is half-filled with liquid, which means the height of the liquid is 1 m (half of 2 m).
2. Identify the Accelerations:
- The box is given a horizontal acceleration of g2.
- There is also a vertical downward acceleration of g2.
- We need to find the additional vertical acceleration ay such that no part of the bottom of the box is exposed.
3. Determine the Effective Gravity:
- When the box accelerates horizontally, the effective gravity acting on the liquid will change due to the horizontal acceleration.
- The effective gravity geff can be calculated using the formula:
geff=g−ay
- In this case, the effective gravity will also include the horizontal acceleration:
geff=g−g2+ay
4. Calculate the Angle of the Liquid Surface:
- The angle θ of the liquid surface due to the horizontal acceleration can be found using:
tan(θ)=height of liquidlength of base=1m6m=16
- Therefore, θ is such that tan(θ)=16.
5. Set Up the Equation for No Exposure:
- For the bottom of the box to remain submerged, the height of the liquid must not exceed the height of the box when the box is accelerating.
- The height of the liquid can be expressed as:
h=16×6=1m
- The effective height of the liquid must equal the height of the box (2 m) when considering the effective gravity.
6. Solve for ay:
- Setting the effective gravity equal to the condition for no exposure:
geff=g−g2+ay=2g
- Rearranging gives:
ay=2g−g+g2=3g2
7. Final Calculation:
- Since the box is accelerating downwards, we need to ensure that the vertical acceleration ay is sufficient to counteract the downward acceleration:
ay=g2
Conclusion:
The vertical acceleration of the box required to ensure that no part of the bottom of the box is exposed is g2.
- The box has a base of 6 m x 6 m and a height of 2 m.
- It is half-filled with liquid, which means the height of the liquid is 1 m (half of 2 m).
- The box is given a horizontal acceleration of g2.
- There is also a vertical downward acceleration of g2.
- We need to find the additional vertical acceleration ay such that no part of the bottom of the box is exposed.
- When the box accelerates horizontally, the effective gravity acting on the liquid will change due to the horizontal acceleration.
- The effective gravity geff can be calculated using the formula:
geff=g−ay
- In this case, the effective gravity will also include the horizontal acceleration:
geff=g−g2+ay
- The angle θ of the liquid surface due to the horizontal acceleration can be found using:
tan(θ)=height of liquidlength of base=1m6m=16
- Therefore, θ is such that tan(θ)=16.
- For the bottom of the box to remain submerged, the height of the liquid must not exceed the height of the box when the box is accelerating.
- The height of the liquid can be expressed as:
h=16×6=1m
- The effective height of the liquid must equal the height of the box (2 m) when considering the effective gravity.
- Setting the effective gravity equal to the condition for no exposure:
geff=g−g2+ay=2g
- Rearranging gives:
ay=2g−g+g2=3g2
- Since the box is accelerating downwards, we need to ensure that the vertical acceleration ay is sufficient to counteract the downward acceleration:
ay=g2
The vertical acceleration of the box required to ensure that no part of the bottom of the box is exposed is g2.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - True/False
1 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - SCQ_TYPE
13 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning
8 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
If the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
The maximum value of water pressure in the box is equal to
View SolutionIf the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
Length of exposed portion of top of box is equal to
View Solution
Knowledge Check
Assuming all the surface to be frictionless. The smaller block m is moving horizontally with acceleration a and vertically downwards with acceleration a. Then magnitude of net acceleration of smaller block m with respect to ground
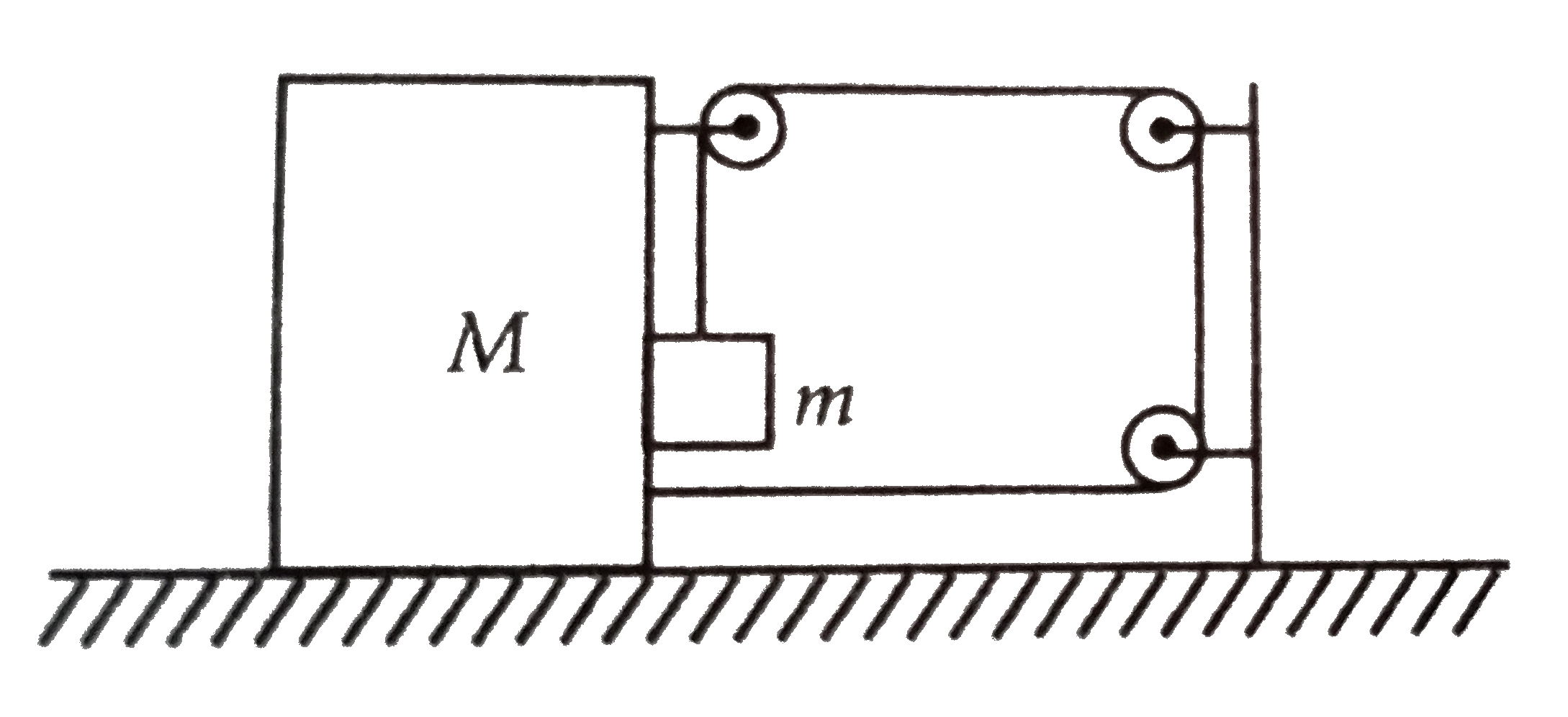 A2√5mg(5m+M)B2mg(5m+M)C7√5gDnone of these
A2√5mg(5m+M)B2mg(5m+M)C7√5gDnone of these
If the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
The angle of the free surface with the horizons is equal to
View SolutionIf the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
Water pressure at the bottomof centre of the box is equal to (atmospheric pressure =105N/m2 density of water =1000kg/m3,g=10m/s2)
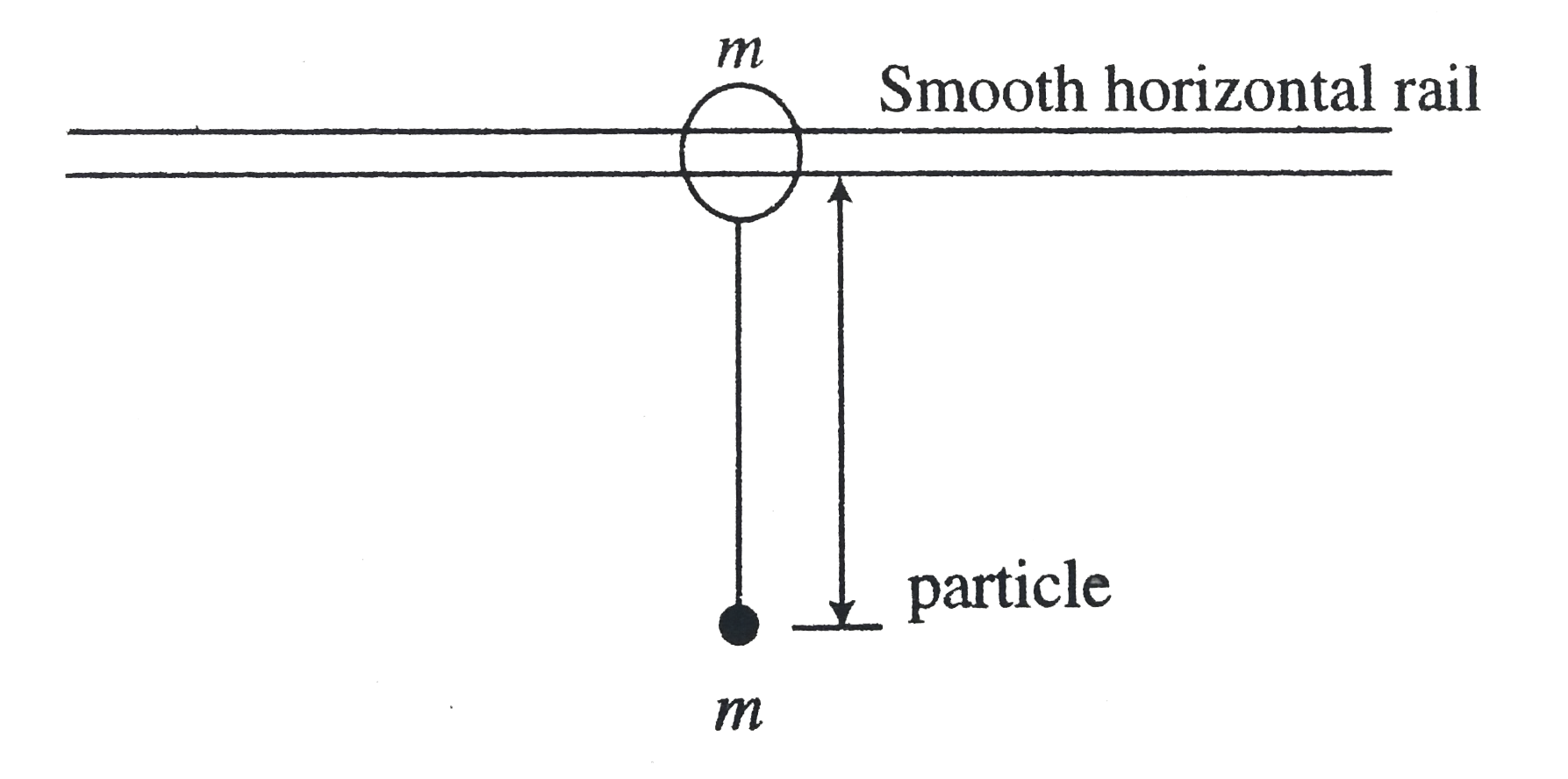
View SolutionThe ring shown in fig. is given a constant horizontal acceleration (a0=g√3). The maximum deflection of the string from the vertical is θ0. Then
View SolutionA liquid kept in a container has a horizontal acceleration 'a' as shown in figure.
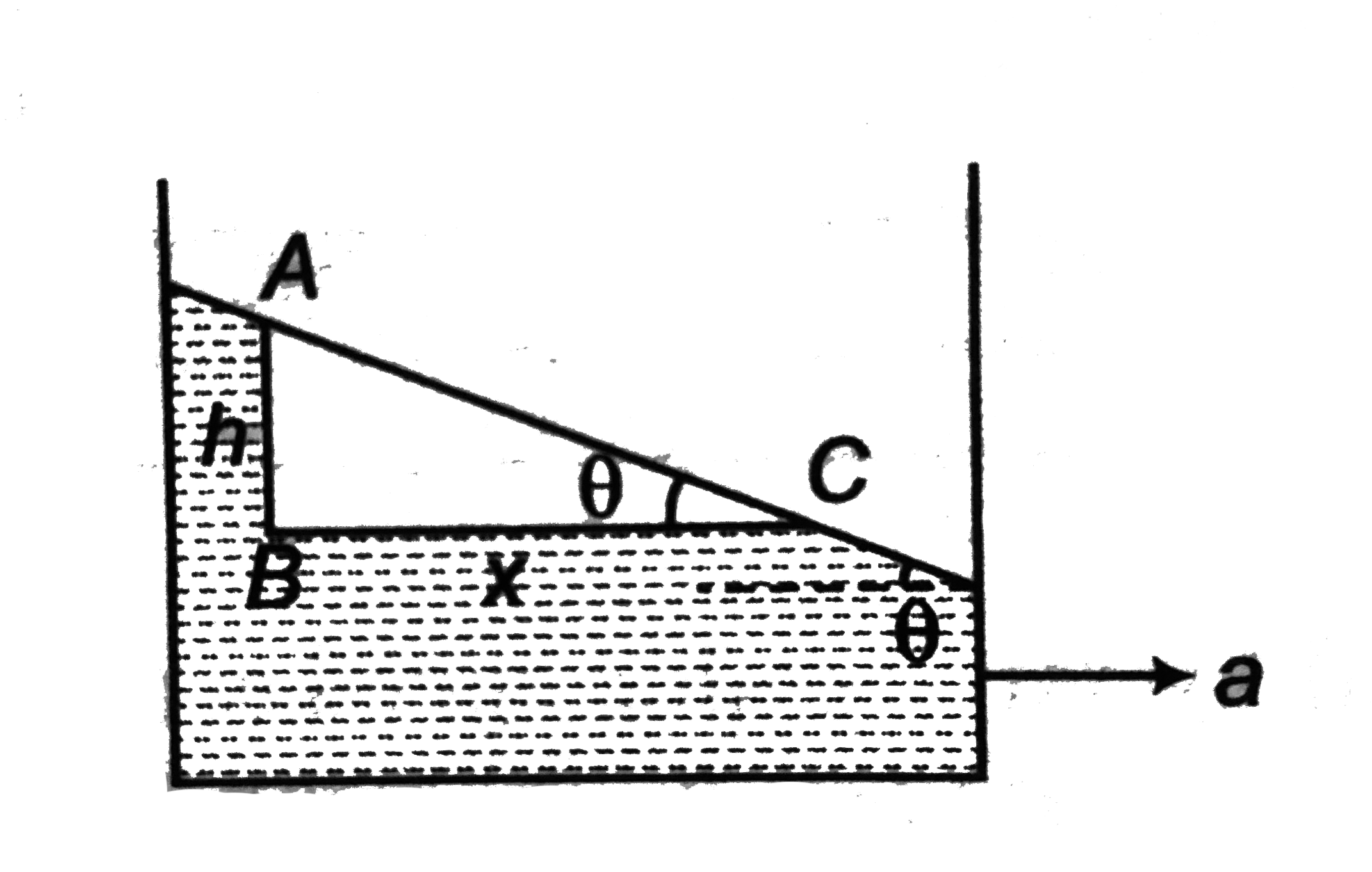
Using the pressure equation along the path ABC find the angle θ.
View SolutionA container shown in Fig. is accelerated horizontally with acceleration a.
a. Find the minimum value of a at which liquid just starts spilling out.

View SolutionA particle is projected horizontally from a tower with velocity u towards east. Wind provides constant horizontal acceleration g2 towards west. If particle strikes the ground vertically the then :

View SolutionFind the period of oscillation of a pendulum of length l if its point of suspension is
(a) moving vertically up with acceleration a
(b) moving vertically down with acceleration a(<g)
(c) failing freely under gravity
moving horizontal with acceleration a.
View Solution
