If the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
The maximum value of water pressure in the box is equal to
1.4MPa
0.14MPa
0.104MPa
0.014MPa
The correct Answer is:B
To find the maximum value of water pressure in the box that is half-filled with liquid and subjected to constant horizontal and vertical accelerations, we can follow these steps:
Step 1: Understand the problem
The box has dimensions of 6 m x 6 m x 2 m and is half-filled with liquid. The box is experiencing a horizontal acceleration of g2 and a vertical downward acceleration of g2. We need to find the maximum pressure at the bottom of the box.
Step 2: Determine the effective gravitational acceleration
When the box is accelerated, the effective gravitational acceleration g′ can be calculated using the formula:
g′=g+a
where a is the acceleration due to the box's motion.
In this case, since the box is accelerating horizontally and vertically downward, we need to consider both components. The effective acceleration will be:
g′=g+g2=g+g2=3g2
Step 3: Calculate the height of the liquid column
Since the box is half-filled with liquid, the height of the liquid column h is:
h=2m2=1m
Step 4: Calculate the maximum pressure
The pressure at a depth in a fluid is given by the formula:
P=Patm+ρg′h
where:
- Patm is the atmospheric pressure (approximately 105Pa),
- ρ is the density of the liquid (for water, ρ≈103kg/m3),
- g′ is the effective gravitational acceleration,
- h is the height of the liquid column.
Substituting the values:
P=105+(103)(3g2)(1)
Using g≈10m/s2:
P=105+(103)(3×102)(1)
P=105+(103)(15)
P=105+15000
P=115000Pa
Step 5: Convert pressure to MegaPascal
To convert the pressure from Pascal to MegaPascal:
P=115000106=0.115MPa
Final Answer
The maximum value of water pressure in the box is:
0.115MPa
The box has dimensions of 6 m x 6 m x 2 m and is half-filled with liquid. The box is experiencing a horizontal acceleration of g2 and a vertical downward acceleration of g2. We need to find the maximum pressure at the bottom of the box.
When the box is accelerated, the effective gravitational acceleration g′ can be calculated using the formula:
g′=g+a
where a is the acceleration due to the box's motion.
g′=g+g2=g+g2=3g2
Since the box is half-filled with liquid, the height of the liquid column h is:
h=2m2=1m
The pressure at a depth in a fluid is given by the formula:
P=Patm+ρg′h
where:
- Patm is the atmospheric pressure (approximately 105Pa),
- ρ is the density of the liquid (for water, ρ≈103kg/m3),
- g′ is the effective gravitational acceleration,
- h is the height of the liquid column.
P=105+(103)(3g2)(1)
Using g≈10m/s2:
P=105+(103)(3×102)(1)
P=105+(103)(15)
P=105+15000
P=115000Pa
To convert the pressure from Pascal to MegaPascal:
P=115000106=0.115MPa
The maximum value of water pressure in the box is:
0.115MPa
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - True/False1videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - SCQ_TYPE13videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning8videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
Similar Questions
If the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
The angle of the free surface with the horizons is equal toView SolutionIf the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
Water pressure at the bottomof centre of the box is equal to (atmospheric pressure =105N/m2 density of water =1000kg/m3,g=10m/s2)View Solution
Knowledge Check
- Question 1 - Select One
Assuming all the surface to be frictionless. The smaller block m is moving horizontally with acceleration a and vertically downwards with acceleration a. Then magnitude of net acceleration of smaller block m with respect to ground
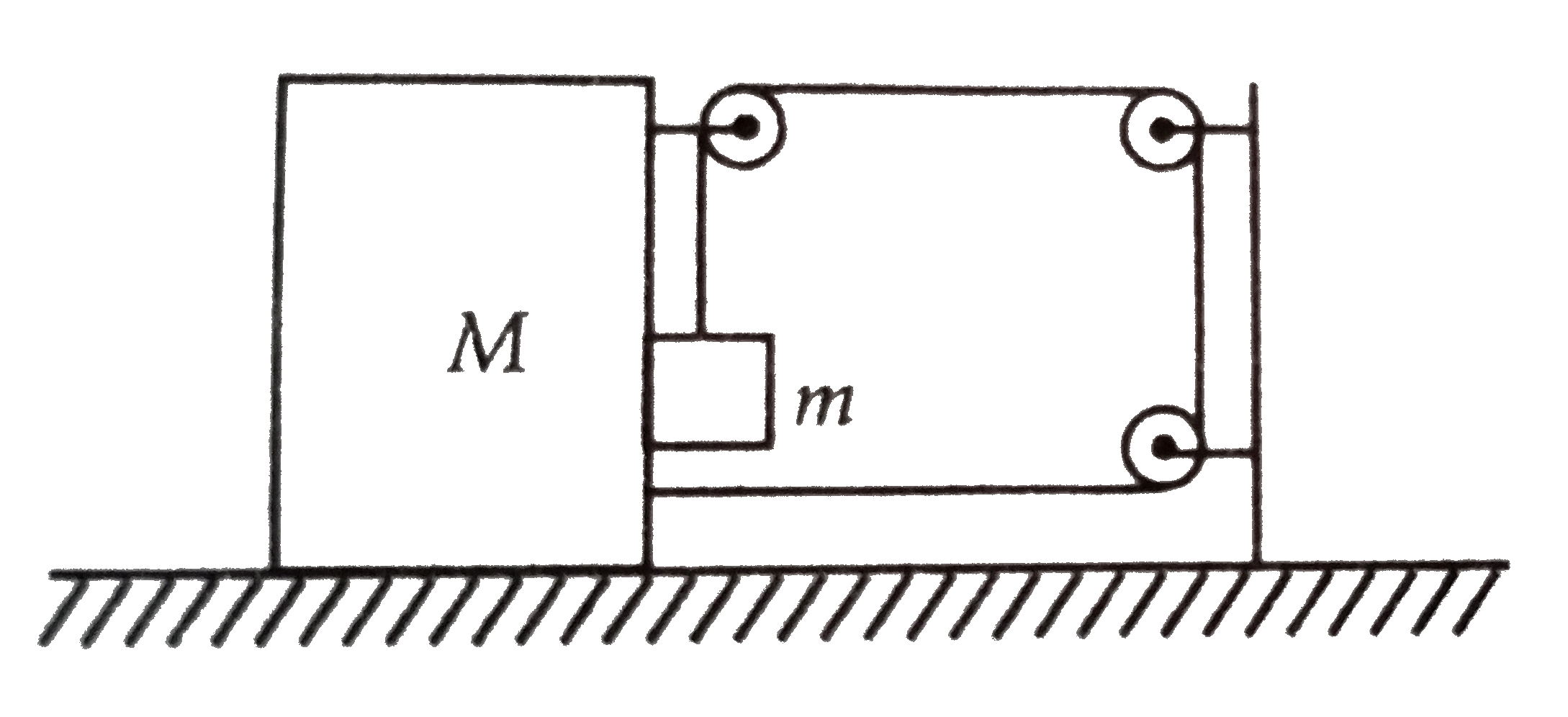 A2√5mg(5m+M)B2mg(5m+M)C7√5gDnone of these
A2√5mg(5m+M)B2mg(5m+M)C7√5gDnone of these
If the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
What is the value of vertical acceleration of box for given horizontal acceleration (g/2), so that no part of the bottom of the box is exposed?View SolutionIf the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
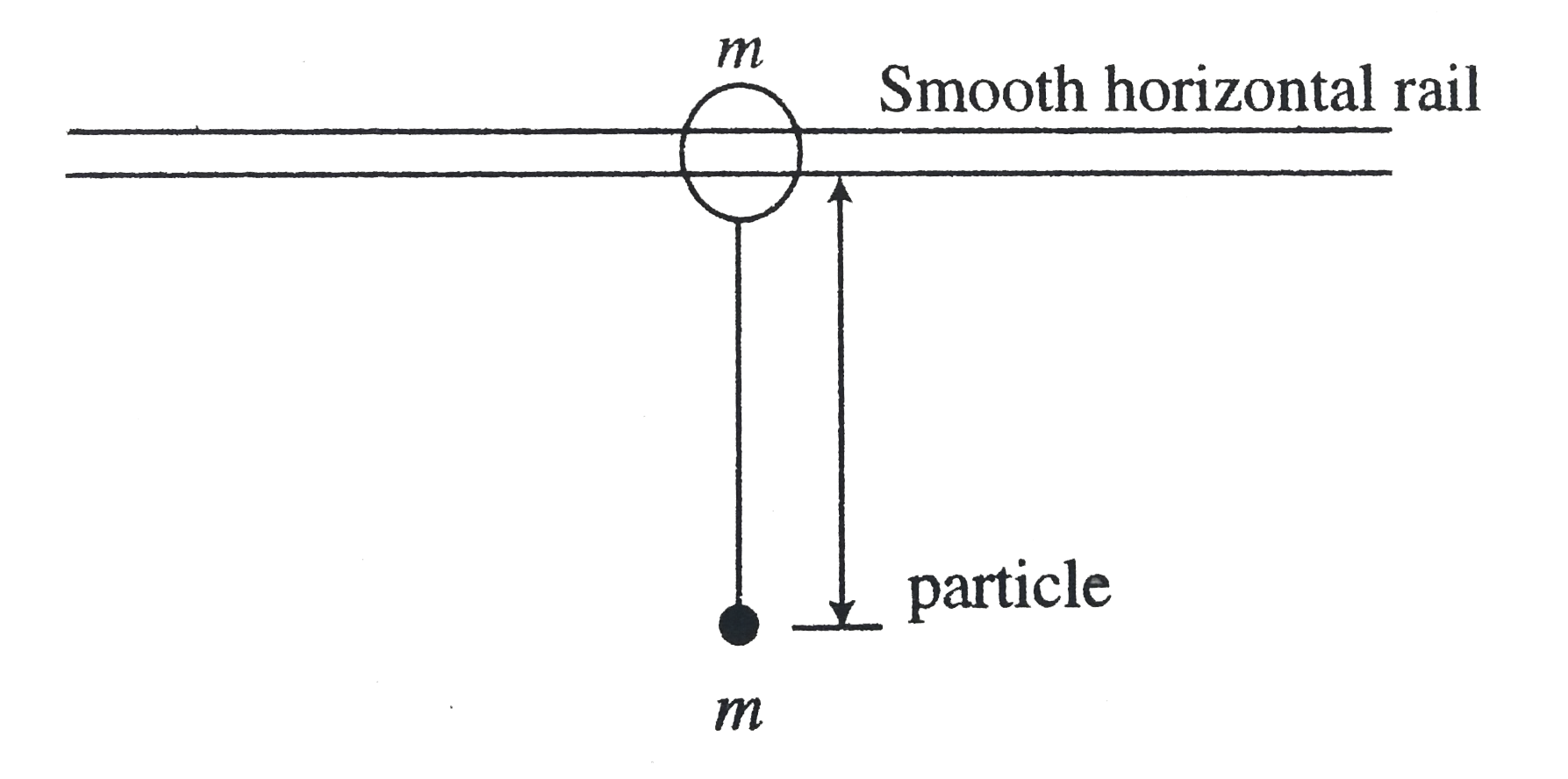
Length of exposed portion of top of box is equal toView SolutionThe ring shown in fig. is given a constant horizontal acceleration (a0=g√3). The maximum deflection of the string from the vertical is θ0. Then
 View Solution
View SolutionA liquid kept in a container has a horizontal acceleration 'a' as shown in figure.
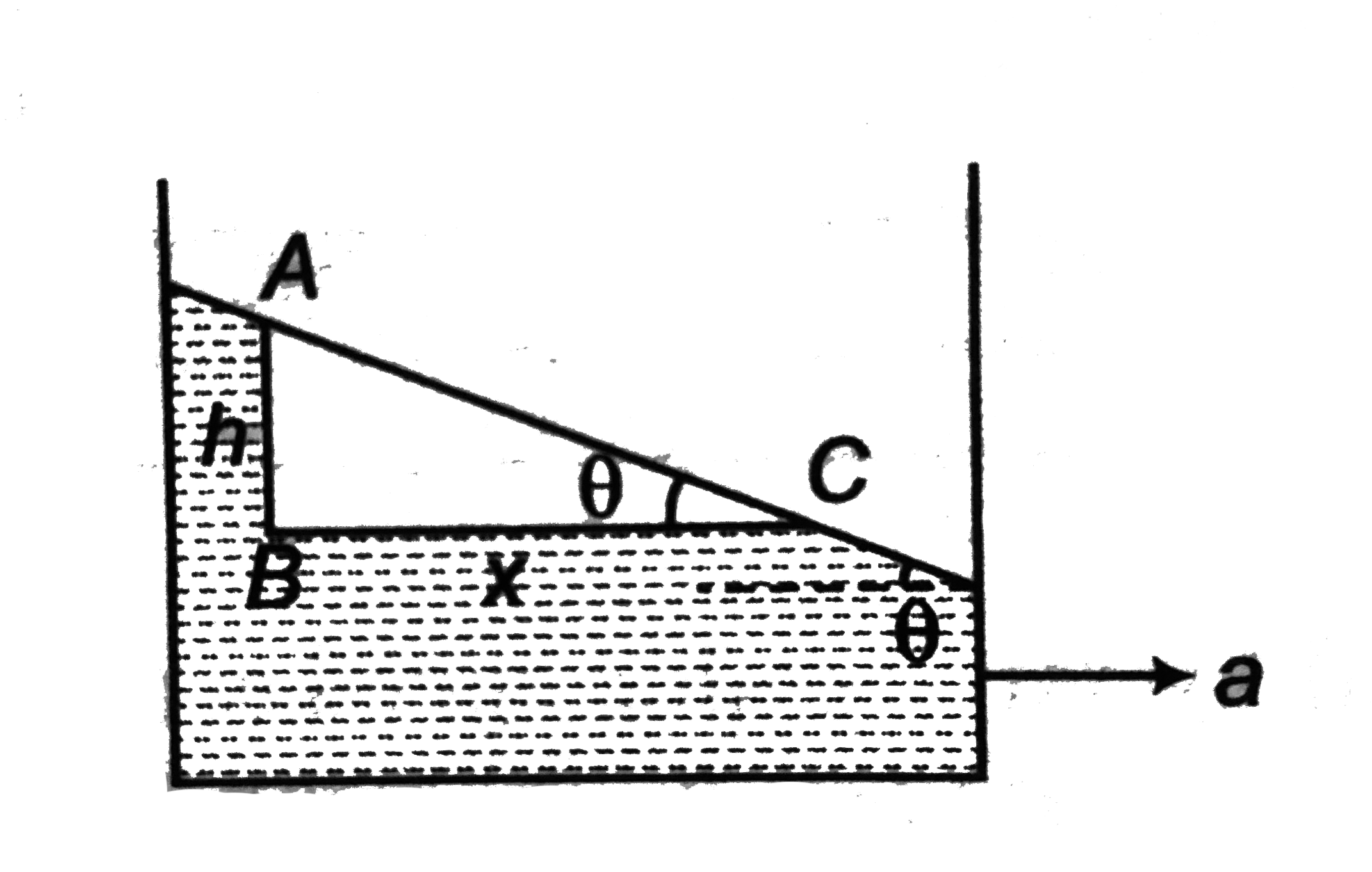
Using the pressure equation along the path ABC find the angle θ.View SolutionA cubical closed vessel of side 5m filled with a liquid is accelerated with an acceleration a. Find the value of a so that pressure at mid pointM of AC is equal to pressure at N.
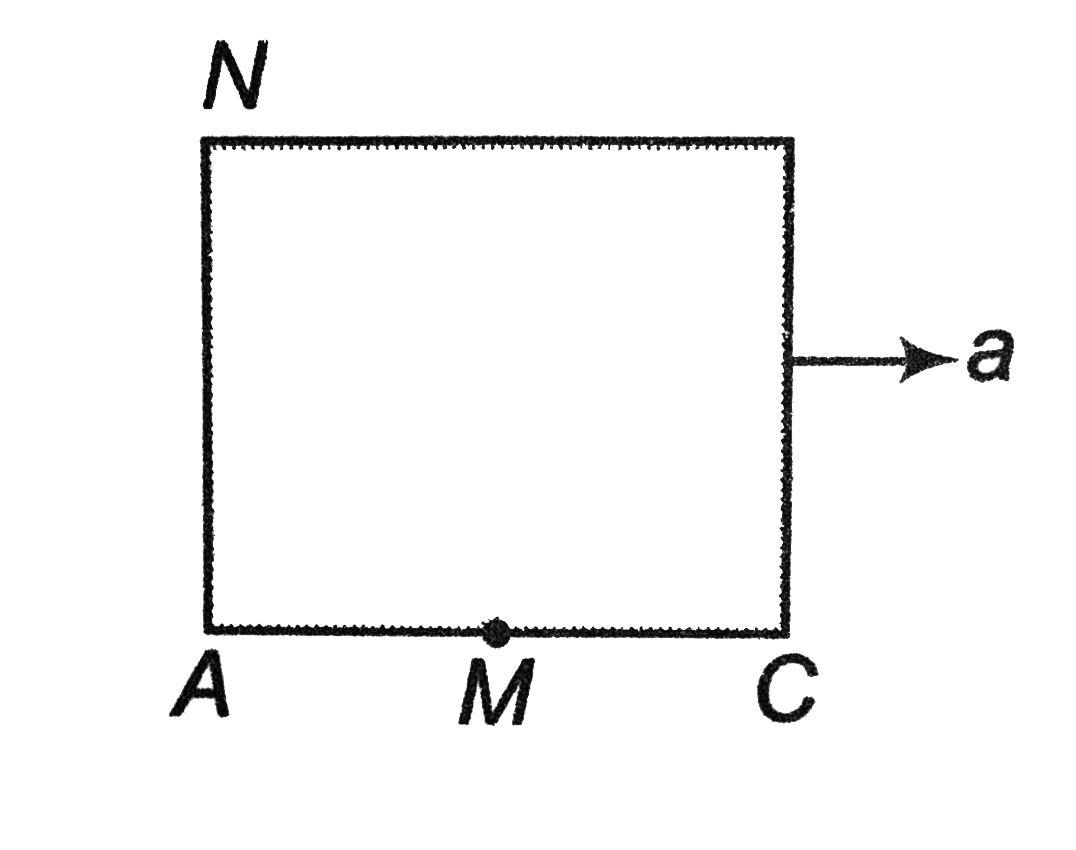 .View Solution
.View SolutionA vessel contains a liquid has a constant acceleration 19.6m/s2 in horizontal direction. The free surface of water get sloped with horizontal at angle
View Solution
A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B isView Solution

