when a proton is released from rest in a room, it starts with an initial acceleration a0 towards west . When it is projected towards north with a speed v0, it moves with an initial acceleration 3a0 towards west. Find the elecrtic field and the minimum possible magnetic field in the room.
To solve the problem step by step, we will analyze the two scenarios given for the proton's motion and derive the electric field and magnetic field accordingly.
Step 1: Analyze the first scenario
When the proton is released from rest, it experiences an initial acceleration a0 towards the west. Since the proton is at rest, the magnetic force acting on it is zero. The only force acting on it is the electrostatic force due to the electric field.
Force Equation:
FE=m⋅a0
Where FE is the electrostatic force, m is the mass of the proton, and a0 is the acceleration towards the west.
According to Coulomb's law, the electrostatic force can also be expressed as:
FE=q⋅E
Where q is the charge of the proton and E is the electric field.
Setting the Forces Equal:
q⋅E=m⋅a0
Step 2: Solve for the electric field E
From the equation above, we can solve for the electric field E:
E=m⋅a0q
Direction of the Electric Field:
The direction of the electric field is towards the west since the proton, being positively charged, accelerates in the direction of the electric field.
Step 3: Analyze the second scenario
In the second scenario, the proton is projected towards the north with a speed v0 and experiences an initial acceleration of 3a0 towards the west. In this case, both the electric force and the magnetic force act on the proton.
Net Force Equation:
The net force acting on the proton can be expressed as:
Fnet=FE+FB
Where FB is the magnetic force.
Since the proton accelerates towards the west with 3a0:
m⋅(3a0)=FE+FB
Step 4: Substitute for FE and FB
From the first scenario, we already know:
FE=m⋅a0
The magnetic force can be expressed as:
FB=q⋅v0⋅B
Where B is the magnetic field.
Substituting the forces:
m⋅(3a0)=m⋅a0+q⋅v0⋅B
Rearranging gives:
m⋅(3a0)−m⋅a0=q⋅v0⋅B
2m⋅a0=q⋅v0⋅B
Step 5: Solve for the magnetic field B
Now, we can solve for B:
B=2m⋅a0q⋅v0
Direction of the Magnetic Field:
The magnetic field direction will be vertically downward, as established from the right-hand rule considering the proton's motion towards the north and the resulting force towards the west.
Final Results
- The electric field E is given by:
E=m⋅a0q(towards west)
- The magnetic field B is given by:
B=2m⋅a0q⋅v0(vertically downward)
When the proton is released from rest, it experiences an initial acceleration a0 towards the west. Since the proton is at rest, the magnetic force acting on it is zero. The only force acting on it is the electrostatic force due to the electric field.
FE=m⋅a0
Where FE is the electrostatic force, m is the mass of the proton, and a0 is the acceleration towards the west.
FE=q⋅E
Where q is the charge of the proton and E is the electric field.
q⋅E=m⋅a0
From the equation above, we can solve for the electric field E:
E=m⋅a0q
Direction of the Electric Field:
The direction of the electric field is towards the west since the proton, being positively charged, accelerates in the direction of the electric field.
In the second scenario, the proton is projected towards the north with a speed v0 and experiences an initial acceleration of 3a0 towards the west. In this case, both the electric force and the magnetic force act on the proton.
The net force acting on the proton can be expressed as:
Fnet=FE+FB
Where FB is the magnetic force.
m⋅(3a0)=FE+FB
From the first scenario, we already know:
FE=m⋅a0
The magnetic force can be expressed as:
FB=q⋅v0⋅B
Where B is the magnetic field.
m⋅(3a0)=m⋅a0+q⋅v0⋅B
Rearranging gives:
m⋅(3a0)−m⋅a0=q⋅v0⋅B
2m⋅a0=q⋅v0⋅B
Now, we can solve for B:
B=2m⋅a0q⋅v0
Direction of the Magnetic Field:
The magnetic field direction will be vertically downward, as established from the right-hand rule considering the proton's motion towards the north and the resulting force towards the west.
- The electric field E is given by:
E=m⋅a0q(towards west)
- The magnetic field B is given by:
B=2m⋅a0q⋅v0(vertically downward)
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - QUESTIONS FOR SHORT ASNWER10videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective29videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective 110videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer11videos
LIGHT WAVES
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer12videos
MAGNETIC FIELD DUE TO CURRENT
Similar Questions
When a proton is released from rest in a room, it starts with an initial acceleration a0 towards west. When it is projected towards north with a speed v0 it moves with an initial accelaration 3a0 towards west. The electric and the maximum possible magnetic field in the room
(i) ma0e, towards west
(ii) 2ma0ev0, downward
(iii) ma0e, towards east
(iv) 2ma0ev0, upwardView SolutionWhen a proton is released from rest in a room, it starts with an initial acceleration a0 towards west. When it is projected towards north with a speed v0 it moves with an initial acceleration 3a0 towards west. The electric and magnetic fields in the room are
View SolutionA ball of density ais released from rest from the centre of an accelerating sealed cubical vessel completely filled with a liquid of density ρ. If the trough moves with a horizontal acceleration →a0 find the initial acceleration of the ball.
View SolutionThe rectangualr wire- frame, shown in has a width d, mass m, resistance R and a large length. A uniform magnetic field B exists to the left of the frame. A constant force F starts pushing the frame into the magnetic field at t =0. (a) Find the acceleration of the frame when its speed has increased to v. (b) Show that after some time the frame will move with a constant velocity till the whole frame enters into the magnetic field. find this velocity v0. (c) show that the velocity at tiem t is given by v=v0(1−e−Ftmv0.
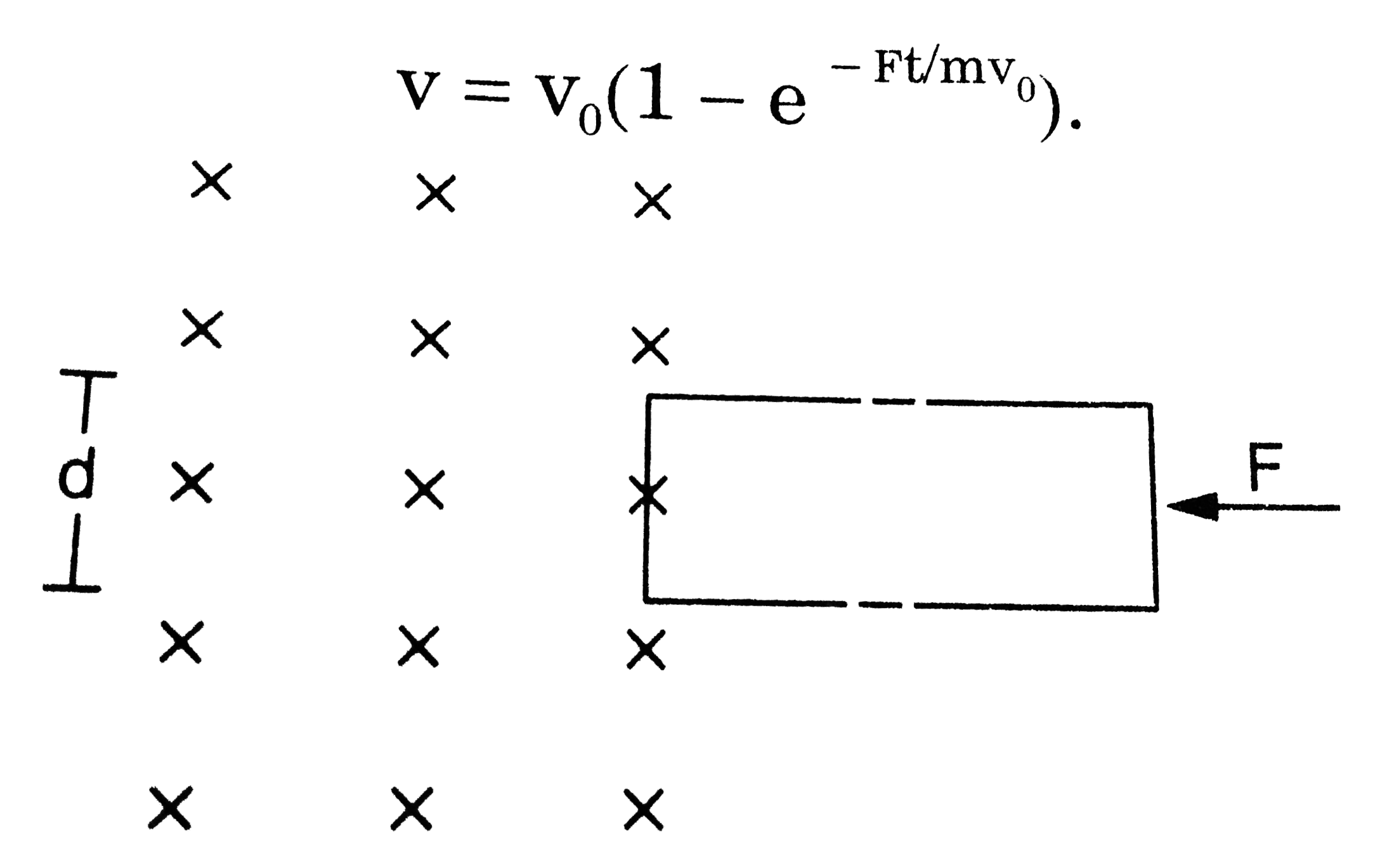 View Solution
View SolutionA particle starts from rest at time t=0 and moves on a straight line with acceleration as plotted in fig. The speed of the particle will be maximum after time.
 View Solution
View SolutionA bus starting from rest moves with a uniform acceleration of 0.1m/s2 for 2 minutes. Find
(a) the speed acquired, (b) the distance travelled.View SolutionThe jet plane starts from rest at s=0 and is subjected to the acceleration shown. Determine the speed of the plane when it has travelled 60 m.
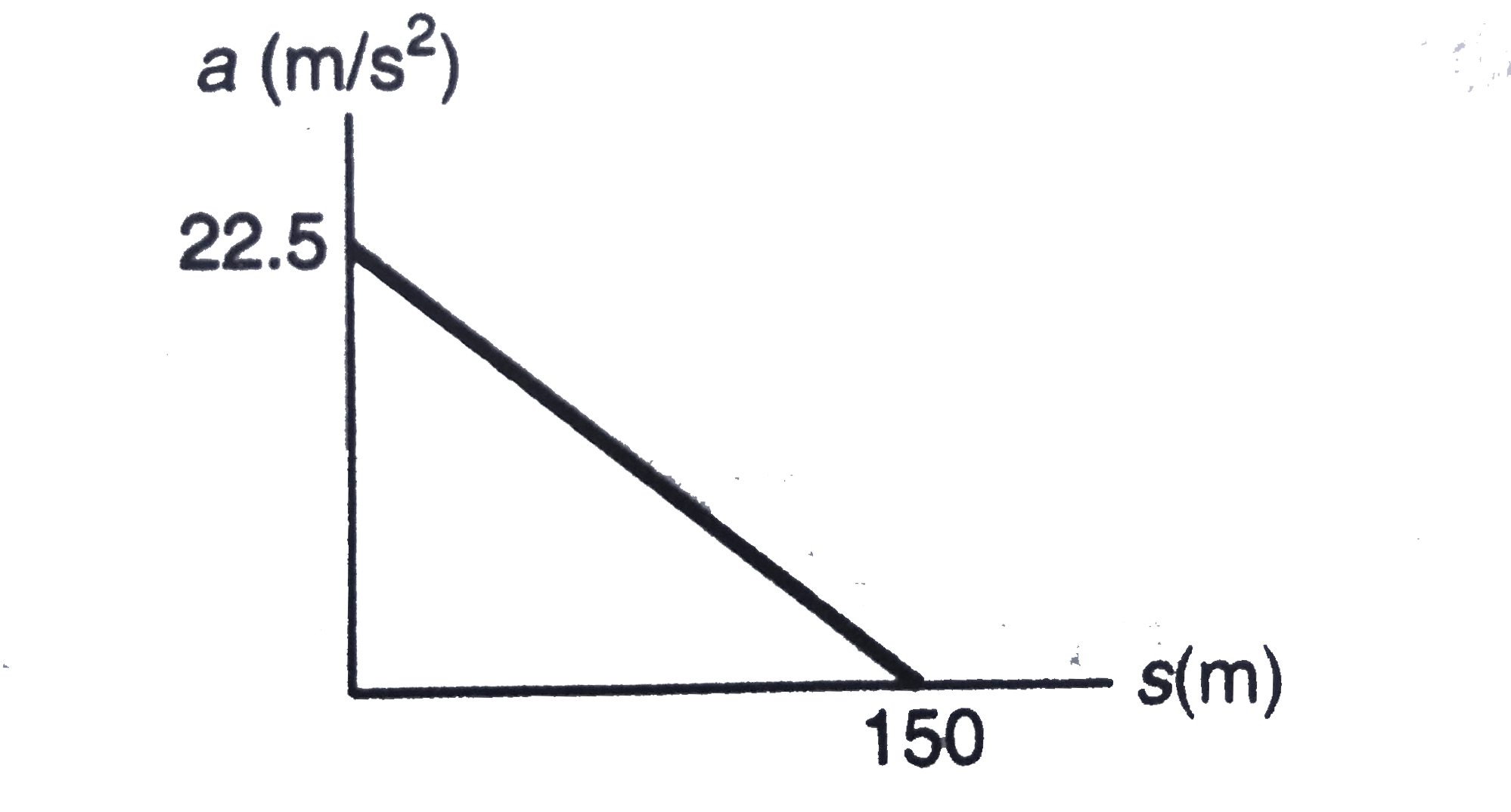 View Solution
View SolutionA particle has a velocity u towards east at t=0. Its acceleration is towards west and is constant. Let xA and xB be the magnitude of displacements in the first 10 seconds and the next 10 seconds
View SolutionA particle has a velocity u towards east at t=0. Its acceleration is towards west and is constant. Let xA and xB be the magnitude of displacement in the first 10 seconds and the next 10 seconds:
View SolutionWhen a charged particle moves in an elecltric or a magnetic field, its speed is v and acceleration is a
View Solution

