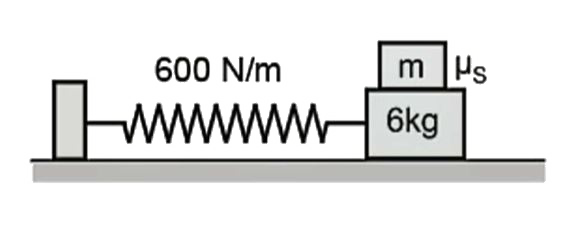
With the assumption of no slipping, determine the mass m of the block which must be placed on the top of a 6kg cart in order that the system period is 0.75s. What is the minimum coefficient of static friction μs for which the block will not slip relative to the cart is displaced 50mm from the equilibrium position and released? Take (g=9.8m/s2).

We know.
T=2π√(m/k)
=2π√(m+6600)
⇒0.75=2π√(m+6600)
m=2.56kg
Maximum acceleration of SHM is amax=ω2A(A=amplitude)
To avoid slipping . Maximum force of mass m is mω2A which is being proveded by the force of friction between blocks A and B
μsmg≥mω2A
⇒μs≥(ω2A)/g
≥(2π/T)2(A/g)
≥(2π0.75)2(0.059.8) (A=50nm)
=0.358
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single Correct
107 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.1
23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
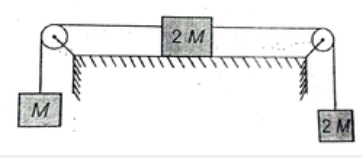
The three blocks in figure are released from rest and accelerate at the rate of 2 ms2. If M = 5 kg , what is the coefficient of friction between the surface and the block B ?
View SolutionA marble block of mass 2 kg lying on ice when given a velocity of 6m/s is stopped by friction in 10s. Then the coefficient of friction is
View Solution
Knowledge Check
A block of mass 2 kg is placed on the floor. The coefficient of static friction is 0.4. A force F of 2.5 N is applied on the block as shown in Fig. 15.4.4. The force of friction between the block and the floor is (g=9.8m/s2)
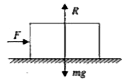 A1.5 NB0.5 NC2.5 NDNone of the above
A1.5 NB0.5 NC2.5 NDNone of the above
A marble block of mass 2 kg lying on ice when given a velocity of 6m/s is stopped by friction in 10s. Then the coefficient of friction is
View SolutionA block of mass 1 kg is placed on a truck which accelerates with acceleration 5ms−2. The coefficient of static friction between the block and truck is 0.6. The frictional force acting on the block is
View SolutionA block of mass m is placed on the top of a 6kg cart such that the time period of the system is 0.75 s assuming there is no slipping. If the cart is displaced by 50 mm from its equilibrium position and released, then the coefficient of static friction μs between block and cart is just sufficient to prevent the block from sliding. The value of m and μs respectively are (Take g=9.8m/s2)
View SolutionA block of mass 2 kg is at rest on a floor . The coefficient of static friction between block and the floor is 0.54. A horizonatl force of 2.8 N is applied to the block . What should be the frictional force between the block and the floor ? ( take , g=10m/s2)
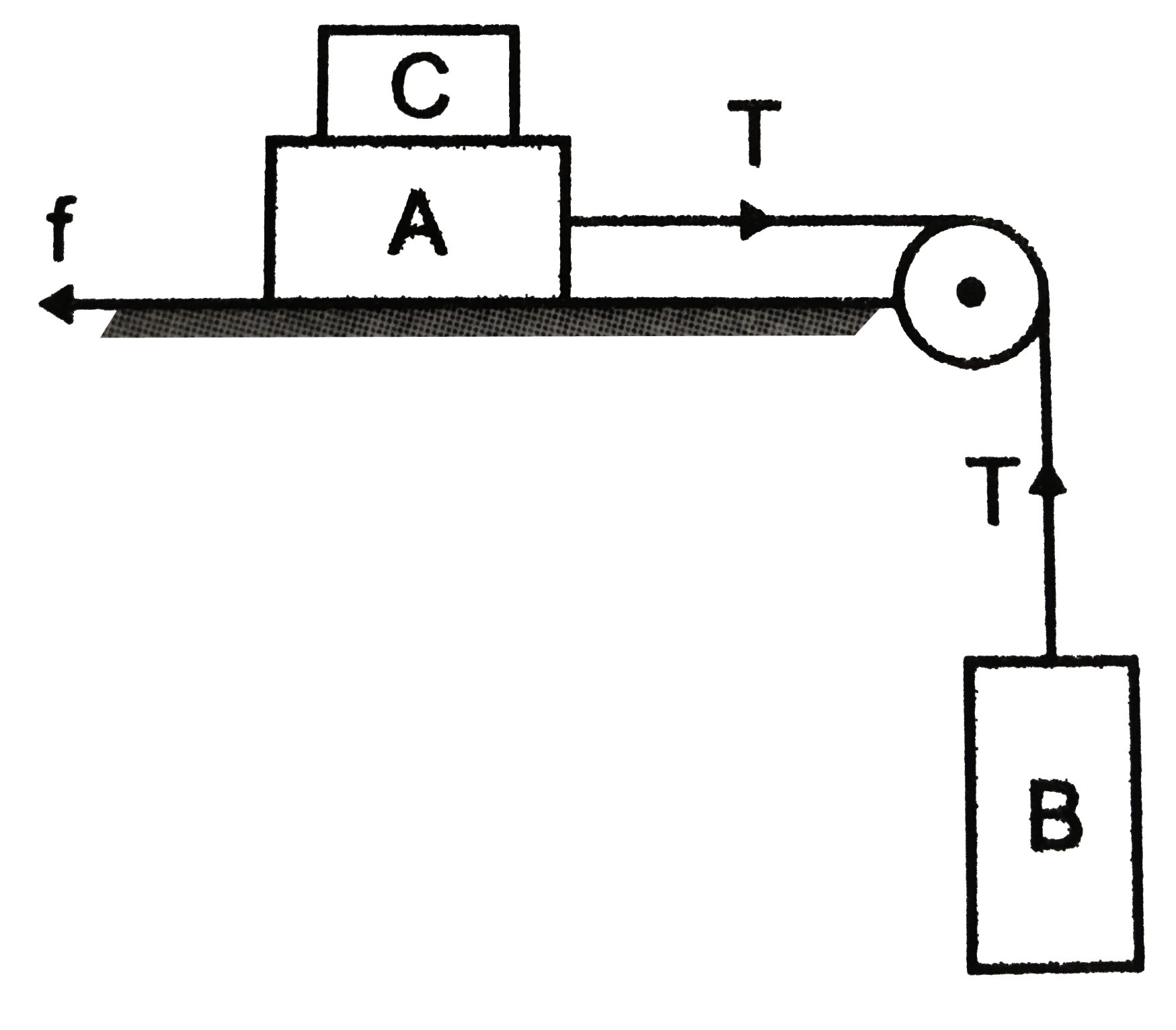
View SolutionIn the masses of A and B are 10 kg and 5 kg . Calculate the minimum mass of C which may stop A from slipping Coefficient of static friction between block A and table is 0.2
 .
.
View SolutionA block of mass 2 kg is placed on the floor . The coefficient of static friction is 0.4 . If a force of 2.8 N is applied on the block parallel to floor , the force of friction between the block and floor is : (Taking g = 10m/s2)
View SolutionA block of mass 2 kg is placed on the floor. The coefficient of static friction it 0.4. A force F of 2.5 N is applied on the block, as shown. calculate the force of friction between the block and the floor. (g=9.8m/s2).
View Solution
