With what minmum speed should be projected from point in presence of two fixed masses each at and as shows in the figure such that mass should escape the gravitational of and ?
The correct Answer is:B
To solve the problem of finding the minimum speed v with which mass m should be projected from point C to escape the gravitational influence of two fixed masses M located at points A and B, we can use the principle of conservation of energy.
1. Understanding the System:
- We have two fixed masses M at points A and B.
- The distance between A and B is 2r.
- The distance from C to both A and B is r√2 (using the Pythagorean theorem).
2. Conservation of Energy:
- The total mechanical energy at point C (initial) must equal the total mechanical energy when mass m is at infinity (final).
- At infinity, the potential energy is zero, and we want the kinetic energy to also be zero for escape.
3. Initial Energy Calculation:
- The initial kinetic energy (KE) when mass m is projected from point C is given by:
KEi=12mv2
- The initial potential energy (PE) due to the gravitational attraction from both masses M is:
PEi=−GMmr√2−GMmr√2=−2GMmr√2
4. Final Energy Calculation:
- At infinity, the final kinetic energy KEf=0 and the potential energy PEf=0.
5. Setting Up the Energy Equation:
- According to the conservation of energy:
KEi+PEi=KEf+PEf
- Substituting the values:
12mv2−2GMmr√2=0
6. Solving for Minimum Speed v:
- Rearranging the equation gives:
12mv2=2GMmr√2
- Dividing both sides by m (assuming m≠0):
12v2=2GMr√2
- Multiplying both sides by 2:
v2=4GMr√2
- Taking the square root:
v=√4GMr√2=2√GM√(4)2⋅√r
Final Answer:
The minimum speed v required for mass m to escape the gravitational influence of the two masses M is:
v=2√GM√(4)2⋅√r
- We have two fixed masses M at points A and B.
- The distance between A and B is 2r.
- The distance from C to both A and B is r√2 (using the Pythagorean theorem).
- The total mechanical energy at point C (initial) must equal the total mechanical energy when mass m is at infinity (final).
- At infinity, the potential energy is zero, and we want the kinetic energy to also be zero for escape.
- The initial kinetic energy (KE) when mass m is projected from point C is given by:
KEi=12mv2
- The initial potential energy (PE) due to the gravitational attraction from both masses M is:
PEi=−GMmr√2−GMmr√2=−2GMmr√2
- At infinity, the final kinetic energy KEf=0 and the potential energy PEf=0.
- According to the conservation of energy:
KEi+PEi=KEf+PEf
- Substituting the values:
12mv2−2GMmr√2=0
- Rearranging the equation gives:
12mv2=2GMmr√2
- Dividing both sides by m (assuming m≠0):
12v2=2GMr√2
- Multiplying both sides by 2:
v2=4GMr√2
- Taking the square root:
v=√4GMr√2=2√GM√(4)2⋅√r
The minimum speed v required for mass m to escape the gravitational influence of the two masses M is:
v=2√GM√(4)2⋅√r
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 2 More Than One Correct
10 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 2 Subjective
14 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 1 Subjective
19 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
Similar Questions
The minimum speed should m be projected from point P in the presence of two fixed spherical masses M each at A and B is shown in the figure such that mass m should escape the gravitational attraction of A and B is x√GMa. Find x.
'(##CEN_KSR_PHY_JEE_C10_031_Q02##)'
View SolutionWith what speed v0 should a body be projected as shown in the figure, with respect to a planet of mass M so that it would just be able to graze the planet and escape ? The radius of the planet is R. (Assume that the planet is fixed ).
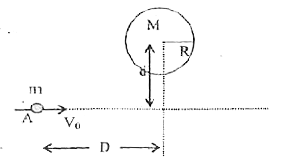
View Solution
Knowledge Check
Two particles are projected with speed 4m/s and 3m/s simultaneously from same point as shown in the figure. Then :
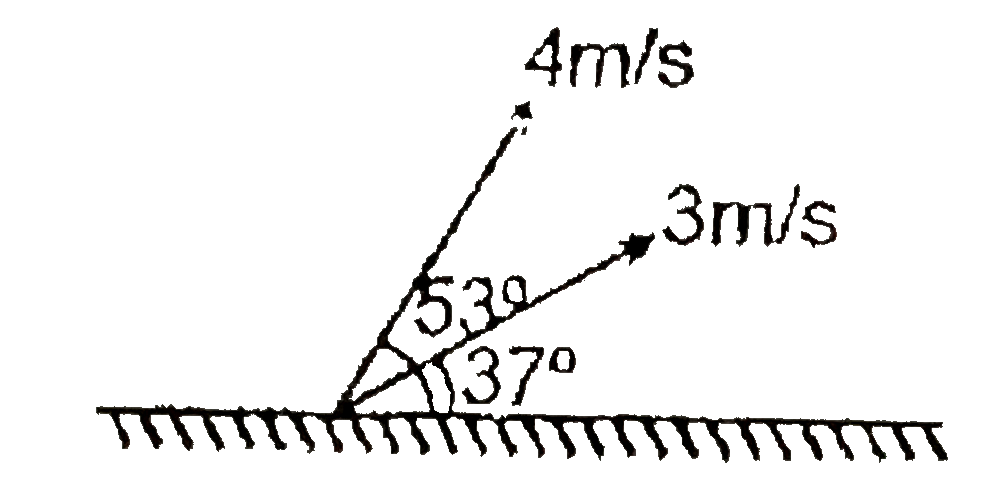 ATheir relative velocity is along horizontal direction.BTheir relative acceleration is non-zero and it is along vertical direction.CThey will hit the surface simultaneously.DTheir relative velocity is constant and has magnitude 1.4m/s
ATheir relative velocity is along horizontal direction.BTheir relative acceleration is non-zero and it is along vertical direction.CThey will hit the surface simultaneously.DTheir relative velocity is constant and has magnitude 1.4m/sA mass m is placed in the cavity inside hollow sphere of mass M as shown in the figure. The gravitational force on m is
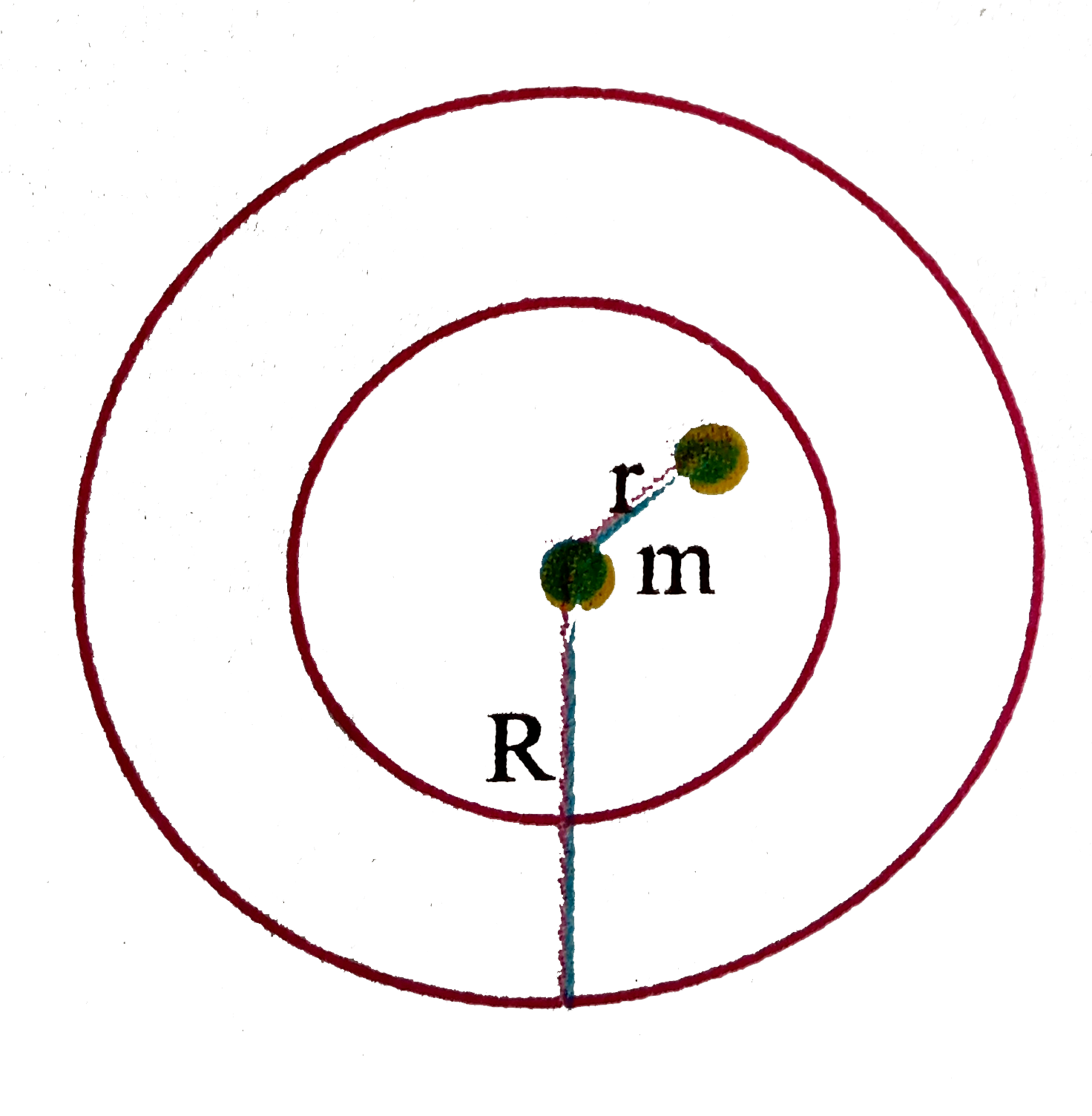 AGMmR2BGMmr2CGMm(R−r)2Dzero
AGMmR2BGMmr2CGMm(R−r)2DzeroTwo point masses m and 2m are kept at points A and B as shown. E represents magnitude of gravitational field strength and V the gravitational potential. As we move from A to B
 AE will first decreases then increasesBE will first increases then decreasesCV will first decreases then increasesDV will first increases then decrease
AE will first decreases then increasesBE will first increases then decreasesCV will first decreases then increasesDV will first increases then decrease
For the equilibrium of the system shown, the value of mass m should be

View SolutionFind the potential V at P in the gravitational field of fixed point mass M.
View SolutionTwo particles are projected with speed 4m/s and 3m/s simultaneously from same point as shown in the figure. Then:

View SolutionFor equilibrium of the system, value of mass m should be

View SolutionA particle is projected from the mid-point of the line joining two fixed particles each of mass m. If the separation between the fixed particles is l, the minimum velocity of projection of the particle so as to escape is equal to
View Solution
