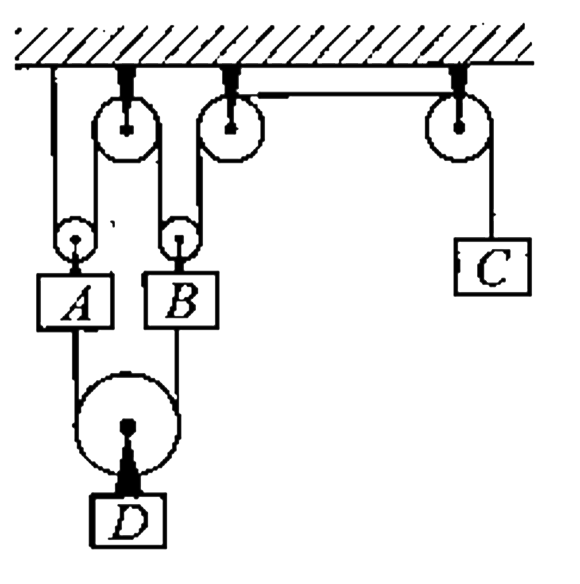
Write equations of forces in terms of the relative acceleration for the blocks shown in and find the relation between m and M so that system remains at rest

Video Solution

Text Solution

Verified by Experts

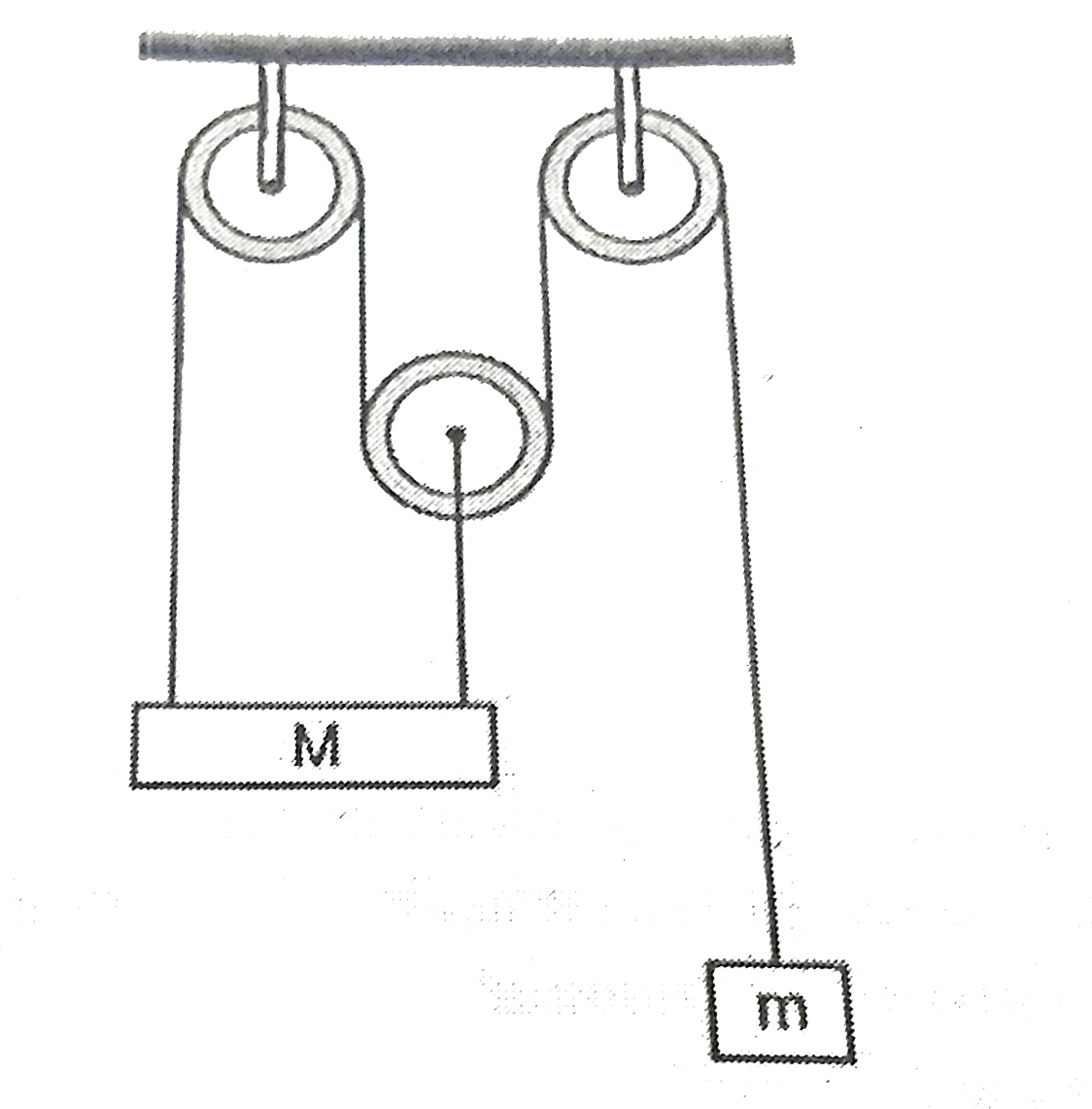
Total length of the cord
$y_{1} + 3 y_{2} + l_{0} = l$
here $y_{1}$ and $y_{2}$ changes $l_{0}$ and l remain constant
Differetiating Eq. (i) with respect to time, we get
$\frac{{d y}_{1}}{d t} + 3 \frac{{d y}_{2}}{d t} = 0$
or $v_{1} + 3 v_{2} = 0$ ....(ii)
also $a_{1} + 3 a_{2} = 0$
which gives $a_{1} = 3 a_{2}$ (magnitude)
if we take $a_{2} = a$ up

then $a_{1} = 3 a$ down
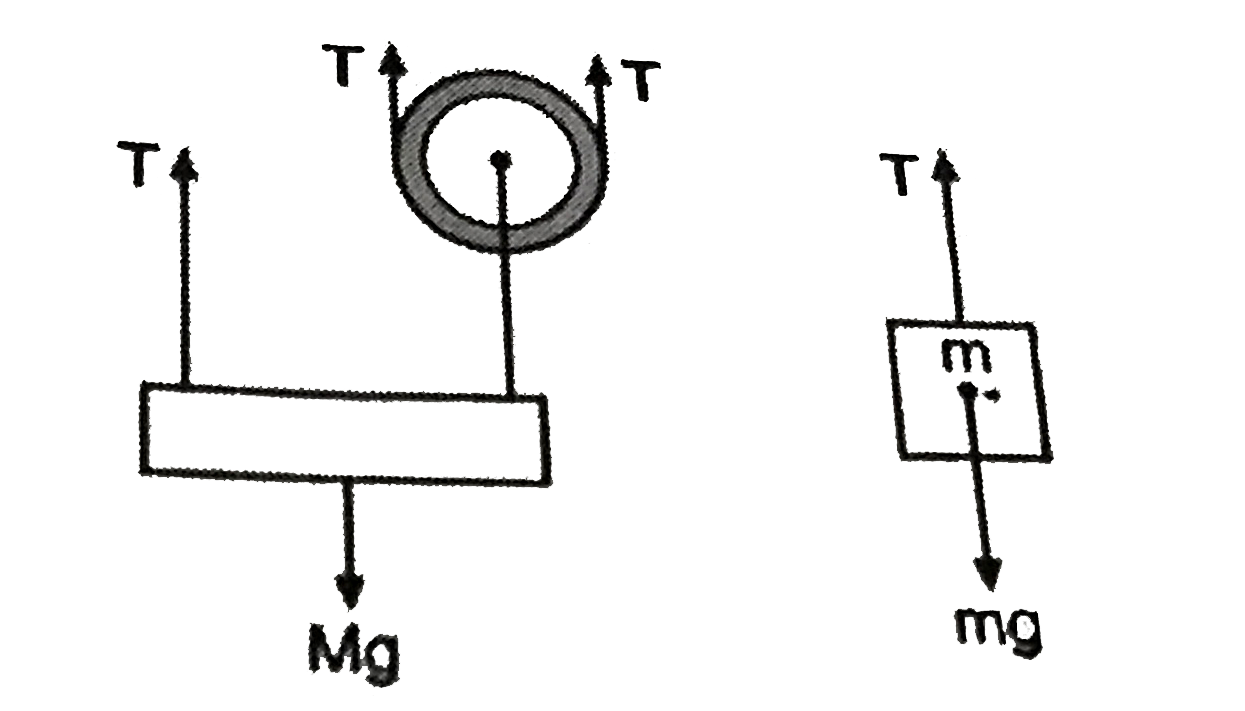
By Newton's second law we have
$m g - T = m (3 a)$ ...(iii)
and $3 T - M g = M a$ ....(iv)
Solving Eqs (iii) and (iv)
$a = \frac{(3 m - M)}{(9 m + M)} g$
if system remains at rest $a = 0$
$∴ 3 m = M$

|

Updated on:21/07/2023

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If system is in equilibrium then find relation between $m_{1}$ and $m_{2}$

A $\frac{m_{1}}{m_{2}} = \frac{1}{2}$
B $\frac{m_{1}}{m_{2}} = \frac{1}{15}$
C $\frac{m_{1}}{m_{2}} = \frac{1}{10}$
D $\frac{m_{1}}{m_{2}} = 1$
Question 2 - Select One
A block of mass m is placed on a smooth inclined wedge ABC of inclination $θ$ as shown in the figure. The wedge is given an acceleration 'a' towards the right. The relation between a and for the block to remain stationary on the wedge is:

A $a = g cos θ$
B $a = \frac{g}{sin θ}$
C $a = \frac{g}{cosec θ}$
D $a = g tan θ$
Question 3 - Select One
A block of mass $m$ is placed on a smooth inclined wedge ABC of inclination theta as shown in the figure. The wedge is given an acceleration $a$ towards the right. The relation between a and theta for the block to remain stationary on the wedge is.

A $a = g tan θ$
B $a = \frac{g}{cos e c θ}$
C $a = cos θ$
D $a = \frac{g}{sin θ}$

GRB PUBLICATION-FORCE AND NEWTONS LAWS OF MOTION-Problem

Home
Ask Doubt
Profile