Write the dimensions of EB. Here, E is the electric field and B the magnetic field.
To find the dimensions of the ratio EB, where E is the electric field and B is the magnetic field, we can follow these steps:
Step 1: Write the dimensions of the electric field E
The electric field E is defined as the force per unit charge. The dimension of force is given by:
Force=mass×acceleration=(M)(L)(T−2)
The dimension of charge Q is simply (Q). Therefore, the dimension of the electric field E can be expressed as:
(E)=(F)(Q)=(M)(L)(T−2)(Q)=(M)(L)(T−2)(Q−1)
Step 2: Write the dimensions of the magnetic field B
The magnetic field B can be defined in terms of the force experienced by a charged particle moving in a magnetic field. The magnetic force on a charged particle is given by:
Force=Q⋅v⋅B⋅sin(θ)
Where v is the velocity of the charged particle. Rearranging gives us:
B=FQ⋅v
Using the dimension of force (F)=(M)(L)(T−2) and the dimension of velocity v=(L)(T), we can write:
(B)=(F)(Q)(v)=(M)(L)(T−2)(Q)⋅(L)(T)=(M)(L)(T−2)(Q)(L)(T−1)=(M)(T−1)(Q−1)
Step 3: Calculate the dimensions of EB
Now, we can find the dimensions of the ratio EB:
EB=(M)(L)(T−2)(Q−1)(M)(T−1)(Q−1)=(M)(L)(T−2)(Q−1)(M)(T−1)(Q−1)=(L)(T−1)
Final Answer
Thus, the dimensions of EB are:
EB=(L)(T−1)
The electric field E is defined as the force per unit charge. The dimension of force is given by:
The magnetic field B can be defined in terms of the force experienced by a charged particle moving in a magnetic field. The magnetic force on a charged particle is given by:
Now, we can find the dimensions of the ratio EB:
Thus, the dimensions of EB are:
Topper's Solved these Questions
- MAGNETICSBook:DC PANDEY ENGLISHChapter:MAGNETICSExercise:SCQ_TYPE
Explore 5 Videos
- MAGNETICSBook:DC PANDEY ENGLISHChapter:MAGNETICSExercise:MCQ_TYPE
Explore 1 Video
- MAGNETICSBook:DC PANDEY ENGLISHChapter:MAGNETICSExercise:SUBJECTIVE_TYPE
Explore 1 Video
- MAGNETIC FIELD AND FORCESBook:DC PANDEY ENGLISHChapter:MAGNETIC FIELD AND FORCESExercise:Medical entrance s gallery
Explore 59 Videos
- MAGNETISM AND MATTERBook:DC PANDEY ENGLISHChapter:MAGNETISM AND MATTERExercise:Medical gallery
Explore 1 Video
Similar Questions
The dimensions of the quantity →E×→B, where →E represents the electric field and →B the magnetic field may be given as :-
View SolutionElectric field induced by changing magnetic fields are
View SolutionAt time t1, an electron is sent along the positive direction of x-axis through both an electric field and a magnetic field, with directed parallel to the y-axis Graph gives the y-component Emax of the net force on the electron due to the two fields, as a function of th eelectron's speed V at time t1. Assuming Bx=0, find magnitude of electric field in mN//C and find z component of magnetic field also (Use e=1.6×10−19C)

View SolutionA He2+ at rest experiences an electromagnetic force. Then (where E is electric field and is B magnetic field)
View SolutionA charge particle travels along a straight line with a speed v in region where both electric field E and magnetic field b are present.It follows that
View SolutionFind the dimensions of
a. electric field E,
magnetic field B and
magnetic permeability μ0
. The relavant equations are
F=qE,FqvB,andB=μ0I2πα,
where F is force q is charge, ν is speed I is current, and α is distance.
View SolutionThe dimension of B22μ0, where B is magnetic field and μ0 is the magnetic permeability of vacuum, is :
View SolutionAn electron enters a region of space in which there exists an electric field 'E' and magnetic field 'B'. If the electron continues to move in the same direction with same velocity as before, the NOT possible case among the following is
View SolutionCan a photon be deflected by an electric field ? By a magnetic field ?
View SolutionIn a region of crossed fields as shown, the strength of electric field is E and that of magnetic field is B. Three positively charged particles with speeds V1,V2andV3 are projected and their paths are shown. From this it implies that
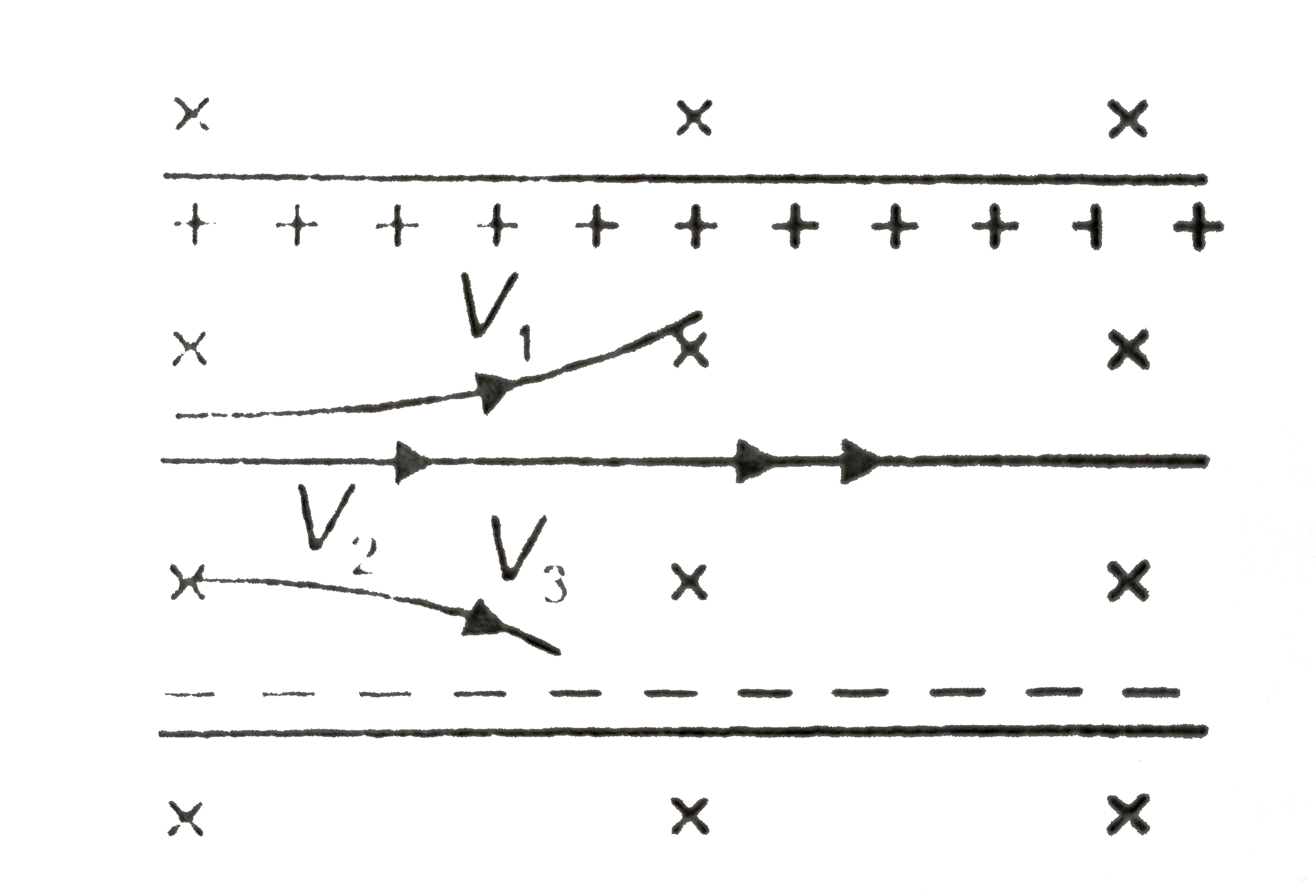
View Solution