A circular loop of wire having a radius of 8.0cm carries a current of 0.20A. A vector of unit length and parallel to the dipole moment W of the loop is given by 0.60ˆi−0.80ˆj . if the loop located in uniform magnetic field given by B=(0.25T)ˆi+(0.30T)ˆk find,
(a) the torque on the loop and
(b) the magnetic potential energy of the loop.
To solve the problem, we need to find the torque on the circular loop and the magnetic potential energy of the loop in the given magnetic field.
Given Data:
- Radius of the loop, R=8.0cm=0.08m
- Current, I=0.20A
- Unit vector parallel to the dipole moment, ^m=0.60^i−0.80^j
- Magnetic field, →B=0.25^i+0.30^k
Step 1: Calculate the Area of the Loop
The area A of the circular loop is given by:
A=πR2
Substituting the radius:
A=π(0.08)2=π(0.0064)≈0.0201m2
Step 2: Calculate the Magnetic Moment →M
The magnetic moment →M is given by:
→M=I⋅A⋅^m
Substituting the values:
→M=0.20⋅0.0201⋅(0.60^i−0.80^j)=0.00402^m
Step 3: Calculate the Torque →τ
The torque →τ on the loop is given by:
→τ=→M×→B
Substituting →M and →B:
→τ=(0.00402^m)×(0.25^i+0.30^k)
Step 4: Calculate the Cross Product
Using the distributive property of the cross product:
→τ=0.00402((0.60^i−0.80^j)×(0.25^i+0.30^k))
Calculating the individual components:
1. ^i×^i=0
2. ^i×^k=^j
3. ^j×^i=−^k
4. ^j×^k=^i
Thus:
→τ=0.00402(0.60⋅0.30^j−0.80⋅0.25(−^k)+0.80⋅0.30^i)
Calculating:
→τ=0.00402(0.18^j+0.20^k+0.24^i)
Final torque:
→τ≈0.000964^i+0.000725^j+0.000804^kN m
Step 5: Calculate the Magnetic Potential Energy U
The magnetic potential energy U is given by:
U=−→M⋅→B
Calculating the dot product:
U=−0.00402((0.60^i−0.80^j)⋅(0.25^i+0.30^k))
Calculating:
U=−0.00402(0.60⋅0.25+0−0)=−0.00402⋅0.15=−0.000603J
Final Answers:
(a) The torque on the loop is approximately →τ≈0.000964^i+0.000725^j+0.000804^kN m.
(b) The magnetic potential energy of the loop is U≈−0.000603J or −0.603mJ.
- Radius of the loop, R=8.0cm=0.08m
- Current, I=0.20A
- Unit vector parallel to the dipole moment, ^m=0.60^i−0.80^j
- Magnetic field, →B=0.25^i+0.30^k
The area A of the circular loop is given by:
A=πR2
Substituting the radius:
A=π(0.08)2=π(0.0064)≈0.0201m2
The magnetic moment →M is given by:
→M=I⋅A⋅^m
Substituting the values:
→M=0.20⋅0.0201⋅(0.60^i−0.80^j)=0.00402^m
The torque →τ on the loop is given by:
→τ=→M×→B
Substituting →M and →B:
→τ=(0.00402^m)×(0.25^i+0.30^k)
Using the distributive property of the cross product:
→τ=0.00402((0.60^i−0.80^j)×(0.25^i+0.30^k))
Calculating the individual components:
1. ^i×^i=0
2. ^i×^k=^j
3. ^j×^i=−^k
4. ^j×^k=^i
→τ=0.00402(0.60⋅0.30^j−0.80⋅0.25(−^k)+0.80⋅0.30^i)
Calculating:
→τ=0.00402(0.18^j+0.20^k+0.24^i)
Final torque:
→τ≈0.000964^i+0.000725^j+0.000804^kN m
The magnetic potential energy U is given by:
U=−→M⋅→B
Calculating the dot product:
U=−0.00402((0.60^i−0.80^j)⋅(0.25^i+0.30^k))
Calculating:
U=−0.00402(0.60⋅0.25+0−0)=−0.00402⋅0.15=−0.000603J
(a) The torque on the loop is approximately →τ≈0.000964^i+0.000725^j+0.000804^kN m.
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SCQ_TYPE
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
Similar Questions
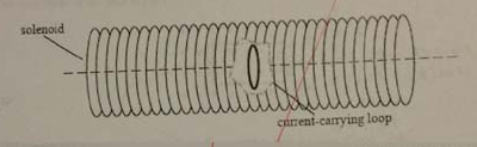
A single circular loop of wire radius 0.02m carries a current of 8.0A. It is placed at the centre of a solenoid that the length 0.65m, radius 0.080m and 1300 turns.
View SolutionA circular loop of area 0.01m2 carrying a current of 10A, is held perpendicular to a magnetic field of intensity 0.1T. The torque acting on the loop is
View SolutionA rectangular loop of sides 20 cm and 10 cm carries a current of 5.0 A. A uniform magnetic field of magnituded 0.20 T exists parallel ot the longer side of the loop (a) What is the force acting on the loop? (b) what is the torque acting on the loop?
View SolutionA circular loop of one turn carries a current of 5.00 A. If the magnetic field B at the centre is 0.200 mT, find the radius of the loop.
View SolutionA magnet of magnetic moment 50ˆiAm2 is placed along the x=axis in a uniform magnetic field →B=(0.5ˆi+3.0ˆj)T . What are the net force and torque experienced by the dipole ?
View SolutionA rectangular loop of metallic wire is of length a and breadth b and carries a current i. The magnetic field at the centre of the loop is
View SolutionA semi circular current loop is placed in an uniform magnetic field of 1 tesla as shown. If the radius of loop is 1 m, the magnetic force on the loop is
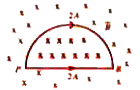
View SolutionA conducting circular loop of radiius r carries a constant current i. It is placed in a uniform magnetic field →B0 such that →B0 is perpendicular to the plane of the loop . The magnetic force acting on the loop is
View SolutionA square loop of sides 10cm carries a current of 10A.A uniform magnetic field of magnitude 0.20T exists parallel to one of the side of the loop.(a)What is the force acting on the loop? (b)What is the torque acting on the loop?
View SolutionThe torque experienced by a given current carrying loop in a uniform magnetic field →B given by B0(ˆi−ˆj) would have magnitude

View Solution
