A particle initially moving towards south in a vertically downward magnetic field is deflected toward the east. What is the sign of the charge on the particle?
To determine the sign of the charge on the particle that is deflected towards the east while moving south in a vertically downward magnetic field, we can follow these steps:
Step 1: Identify the Directions
- The particle is moving towards the south. We can represent this direction as negative y-axis (−j).
- The magnetic field is directed vertically downward, which we can represent as negative z-axis (−k).
- The deflection of the particle is towards the east, which we can represent as positive x-axis (+i).
Step 2: Use the Right-Hand Rule
The force on a charged particle moving in a magnetic field is given by the equation:
→F=q(→v×→B)
Where:
- →F is the magnetic force,
- q is the charge of the particle,
- →v is the velocity vector,
- →B is the magnetic field vector.
Step 3: Determine the Cross Product
Using the right-hand rule, we can find the direction of the force:
1. Point your fingers in the direction of the velocity (south, which is -j).
2. Curl your fingers in the direction of the magnetic field (downward, which is -k).
3. Your thumb will point in the direction of the force.
Calculating the cross product:
- →v=−j
- →B=−k
Using the right-hand rule:
→v×→B=(−j)×(−k)=j×k=i
This indicates that the force is directed towards the east (+i).
Step 4: Determine the Sign of the Charge
Since the force is directed towards the east and we have calculated →F=q(→v×→B) to also point east, we can conclude:
- If q is positive, the force will be in the direction of →v×→B.
- If q is negative, the force would be in the opposite direction.
Since the force is indeed directed towards the east, this indicates that the charge q must be positive.
Conclusion
The sign of the charge on the particle is positive.
---
- The particle is moving towards the south. We can represent this direction as negative y-axis (−j).
- The magnetic field is directed vertically downward, which we can represent as negative z-axis (−k).
- The deflection of the particle is towards the east, which we can represent as positive x-axis (+i).
The force on a charged particle moving in a magnetic field is given by the equation:
→F=q(→v×→B)
Where:
- →F is the magnetic force,
- q is the charge of the particle,
- →v is the velocity vector,
- →B is the magnetic field vector.
Using the right-hand rule, we can find the direction of the force:
1. Point your fingers in the direction of the velocity (south, which is -j).
2. Curl your fingers in the direction of the magnetic field (downward, which is -k).
3. Your thumb will point in the direction of the force.
- →v=−j
- →B=−k
→v×→B=(−j)×(−k)=j×k=i
This indicates that the force is directed towards the east (+i).
Since the force is directed towards the east and we have calculated →F=q(→v×→B) to also point east, we can conclude:
- If q is positive, the force will be in the direction of →v×→B.
- If q is negative, the force would be in the opposite direction.
The sign of the charge on the particle is positive.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SCQ_TYPE5videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE1videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE1videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery1videos
MAGNETISM AND MATTER
Similar Questions
Assertion : A beam of protons is moving towards east in vertically upward magnetic field. Then, this beam will deflect towards south.
Reason : A constant magnetic force will act on the proton beam.View SolutionA charged particle of mass m is moving with a speed u in a circle of radius r. If the magnetic field induction at the centre is B, the charge on the particle is
View Solution
Knowledge Check
- Question 1 - Select One
A charged particle is moving on circular path with velocityv in a uniform magnetic field B, if the velocity of the charged particle is doubled and strength of magnetic field is halved, then radius becomes
A8 timesB4 timesC2 timesD16 times
An electron moving towards the east enters a magnetic field directed towards the north. The force on the electron will be directed
View SolutionA charge +Q is moving upwards vertically. It enters a magnetic field directed to the north. The force on the charge will be towards
View SolutionFour particles enter a region of uniform magnetic field. Their trajectories are shown in figure. What are the signs of the charge of all four particles ?
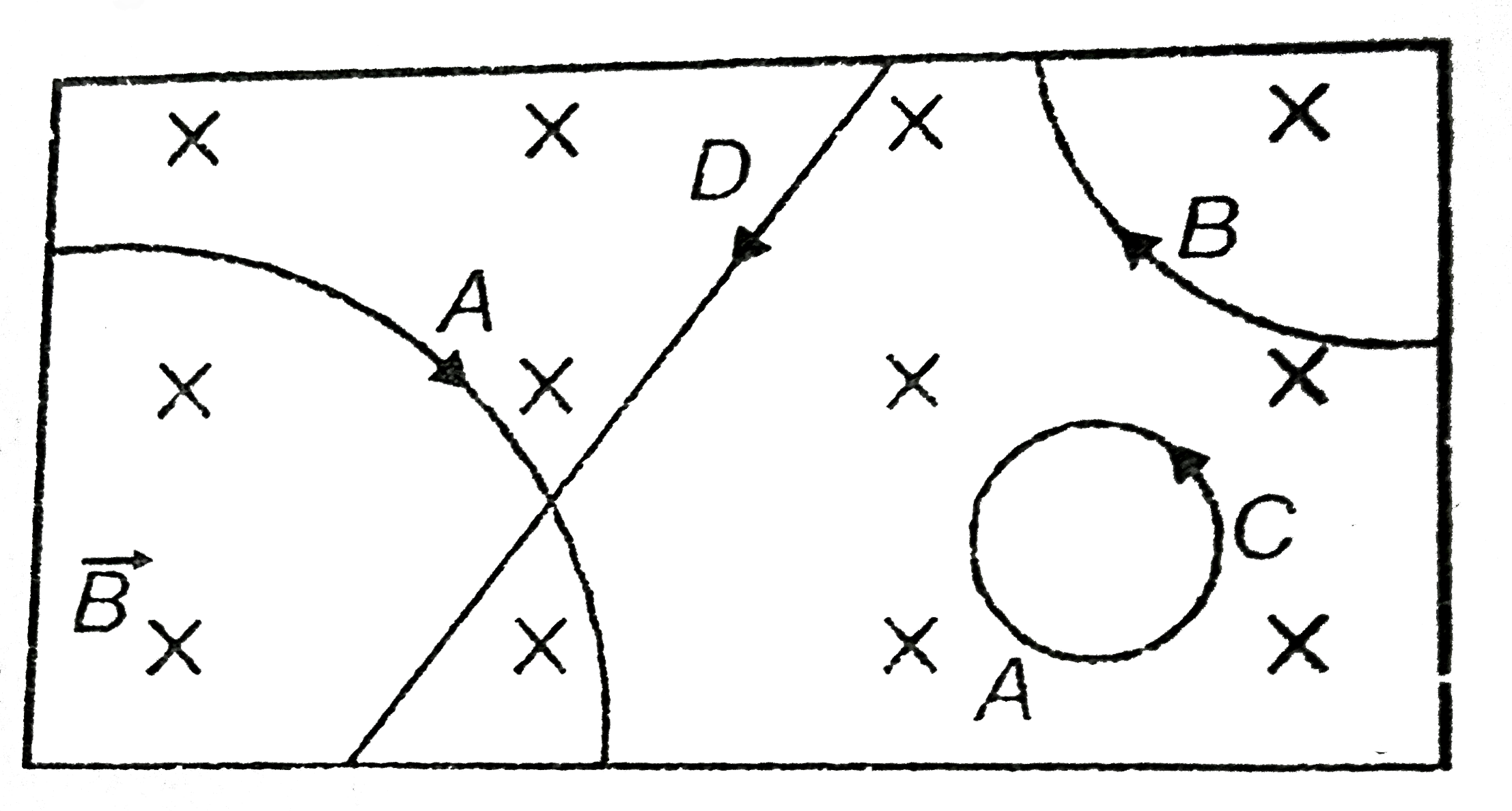 View Solution
View SolutionPositively charged particles are projected into a magnetic field. If the direction of the magnetic field is along the direction of motion of the charged particles, the particles get
View SolutionA charged particle moves in a uniform magnetic field. The velocity of the particle at some instant makes an acute angle with the magnetic field. The path of the particle will be
View SolutionA particle of mass m moving towards west with speed v collides with another particle of mass m movies towards south. If two particles st ich t o each other the speed of the new particle of mass 2 m will be
View SolutionA bird is flying towards south with a velocity 40km/hr and a train is moving with a velocity 40km/hr towards east. What is the velocity of the bird w.r.t. an obserber in train:-
View Solution

