YDSE is carried with two thin sheets of thickness 10.4 m each and refractive index covering the slits respectively. If white light of range 400nm to 780 nm is used, then which wavelength will form maxima exactly at point O, the centre of the screen

only
only
only
The correct Answer is:D
Step by step video & image solution for YDSE is carried with two thin sheets of thickness 10.4mu m each and refractive index mu_1 = 1.52 and mu_2 = 1.40 covering the slits S_1 and S_2 respectively. If white light of range 400nm to 780 nm is used, then which wavelength will form maxima exactly at point O, the centre of the screen by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -III (DIFFRACTION)11videos
WAVES OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -III (POLARISITION)10videos
WAVES OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -II (POLARISATION)10videos
WAVES OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)15videos
WAVES
Similar Questions
In YDSE's experiment performed in a medium of refractive index (4/3), a light of 60 nm wavelength is falling ono the slits having 0.45 mm separation.t he lower slit S2 is covered by a thin glass sheet of thickness 10.4μm and refractive index 1.5 the interference pattern is observed on a screen palced 1.5m from the slits as shown int hef ignore dispersion.
Q. If white light of range 400-700 nm has replaced 600 nm light, one of the wavelengths of light that forms maxima exactly at point O wll be:
 View Solution
View SolutionIn the YDSE shown the two slits are covered with thin sheets having thickness t & 2t and refractive index 2μ and μ .Find the position (y) of central maxima.
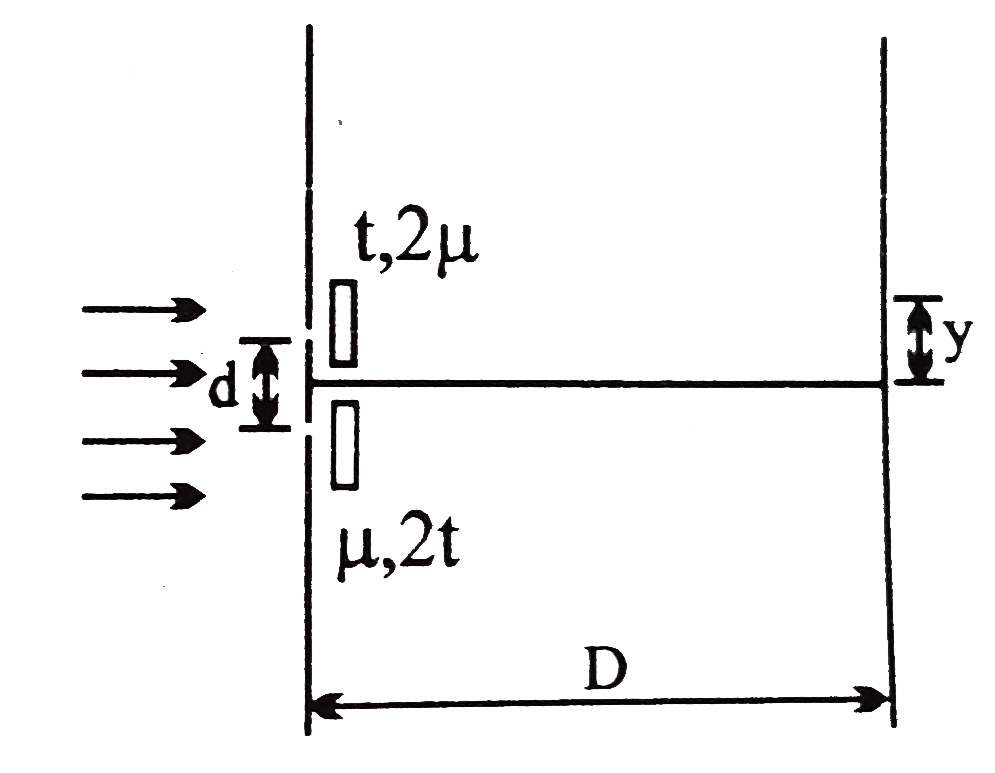 View Solution
View SolutionA beaker is filled with two immiscible transparent liquids of refractive indices μ1 and μ2 having thickness of layers d1 and d2 respectively. The apparent depth of the bottom of the beaker is
View SolutionA thin mica sheet of thickness 2×10−6m and refractive index (μ=1.5) is introduced in the path of the first wave. The wavelength of the wave used is 5000Å. The central bright maximum will shift
View SolutionA thin mica sheet of thickness 2×10−6m and refractive index (μ=1.5) is introduced in the path of the first wave. The wavelength of the wave used is 5000Å. The central bright maximum will shift
View SolutionA thin mica sheet of thickness 2×10−6m and refractive index (μ=1.5) is introduced in the path of the first wave. The wavelength of the wave used is 5000Å. The central bright maximum will shift
View SolutionThe Young's double-slit experiment is done in a medium of refractive index 4/3. A light of 600 nm wavelength isfalling on the slits having 0.45 mm separation. The lower shift S2 is covered by a thin glass sheet of refractive index. 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in Figure
a. Find the location of central maximum (bright fringe with zero path difference) on the y-axis.
b. Find the light intensity of point O relative to the maximum fringe intensity.
c. Now , if 600 nm light is replaced by white light of range 400 - 700 nm, find the wavelengths of the light that from maxima exaclty at point O.
(All wavelength in the problem are for the given medium of refractive index 4/3 Ignoe dispersion.)
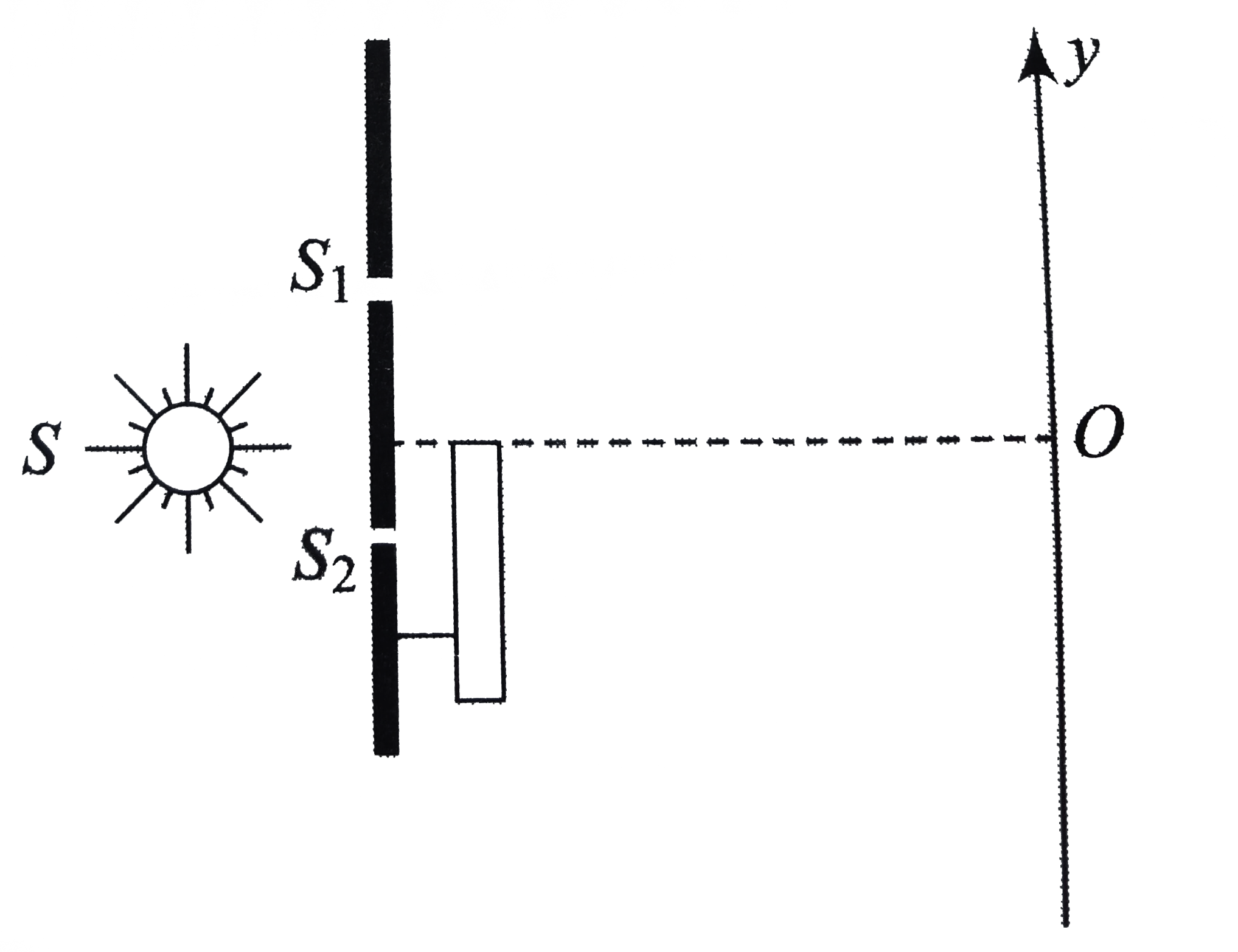 View Solution
View SolutionIn Young's double slit experiment S1 and S2 are two slits. Films of thickness t1 and t2 and refractive indices μ1 and μ2 are placed in front of S1 and S2 respectively. If μ1t1=μ2t2, then the central maximum will :
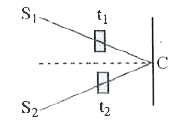 View Solution
View SolutionA thin mica sheet of thickness 4×10−6 m and refractive index (μ=1.5) is introduced in the path of the light from upper slit. The wavelength of the wave used is 5000Å The central bright maximum will shift
View SolutionA monochromatic light of λ=500nm is incident on two identical slits separated by a distance of 5×10−4m. The interference pattern is seen on a screen placed at a distance of 1m from the plane of slits. A thin glass plate of thickness 1.5×10−6m and refractive index μ=1.5 is placed between one of the slits and the screen. Find the intensity at the center of the screen if the intensity is I0 in the absence of the plate. Also find the lateral shift of the central maxima and number of fringes crossed through center.
View Solution

