ABCD is a cyclic quadrilateral in which ∠BAD=750, ∠ABD=580and ∠ADC=770, AC and BD intersect at P. then, find ∠DPC
Video Solution
Text Solution
ABCD, is a cyclic quadrilateral
∠BAD+∠BCD=1800
750+∠BCD=1800
∠BCD=1800−750=1050
∠ADC+∠ABC=1800
770+∠ABC=1800
∠ABC=1800−770=1030
∠DBC=∠ABC−∠ABD
⇒1030−580=450
arcAB subtends ∠ABDand ∠ACD is the same segment.
∠ABD=∠ACD=580
∠ACB=∠BCD−∠ACD=1050−580=470
Now in ,△PBC , ext. ∠DPC=∠PBC+∠PCB
⇒∠DBC+∠ACB=450+470=920
Hence, ∠DPC=920
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If ABCD is a cyclic quadrilateral with ∠A=50∘,∠B=80∘, then Cand∠D are
A100∘,130∘B115∘,115∘C110∘,120∘D130∘,100∘ - Question 2 - Select One
In a cyclic quadrilateral ABCD∠A+∠B+∠C+∠D=?
AA)90∘BB)360∘CC)180∘DD)120∘
ABCD is a cyclic quadrilateral such that ∠ADB=300and ∠DCA=800, the ∠DAB= 700 (b) 1000 (c) 1250 (d) 1500
View SolutionIn Figure, if AB∣∣CD, ∠APQ=500AND ∠PRD=1270, find x and y
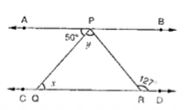 View Solution
View SolutionIn Figure, ABCD is a quadrilateral in which diagonal AC=84 cm ; DL⊥AC, BM⊥AC, DL=16.5 cm and BM=12 cm . Find the area of quadrilateral ABCD.
View SolutionABCD is a cyclic quadrilateral whose diagonals AC and BD intersect at P. If AB=DC, prove that:
(i)PAB ≅PDC
(ii)PA=PD and PC=PB (iii) AD∣∣BCView SolutionIn Figure, ABCD is a parallelogram in which ∠DAO=400, ∠BAO=350 and ∠COD=650. Find: ∠ABO (ii) ∠ODC (iii) ∠ACB (iv) ∠CBD
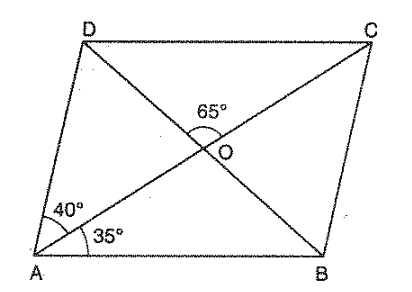 View Solution
View SolutionIn Fig. 71, if ABCD and CDEF, find ∠ACE
View Solution

