ABCD is a square A≡(1,2),B≡(3,−4). If line CD passes through (3,8), then the midpoint of CD is (a) (2, 6) (b) (6,2) (c) (2,5) (d) (285,15)Solution in Bengali
(2,6)
(6,2)
(2,5)
(28/5,1/5)
The correct Answer is:D
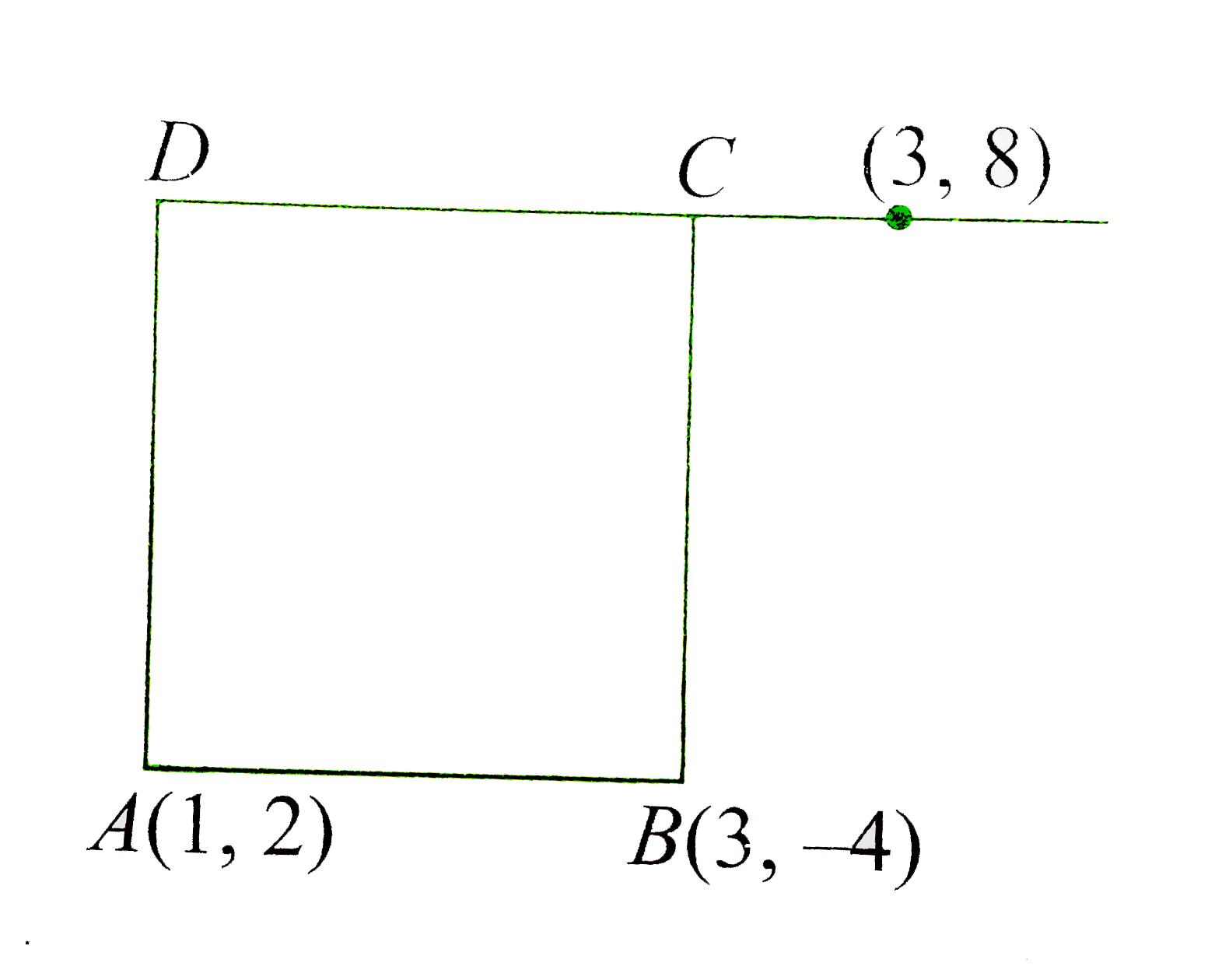
mAB=−4−23−1=−3
Thus, the equation of CD is y-8
=-3(x-3), i.e., y+3x=17. The equation of the right bisector of AB is
y+1=13(x−2)
or 3y=x-5
Solving it with line CD, we get x=28/5, y=1/5. Thus, the midpoint of CD is (28/5,1/5).
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)30videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (LINKED COMPREHENSION TYPE)27videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.65videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
If P is a point (x,y) on the line y=−3x such that P and the point (3, 4) are on the opposite sides of the line 3x−4y=8, then x>815 (b) x>85 y<−85 (d) y<−815
06:26View SolutionLet l be the line belonging to the family of straight lines (a+2b)x+(a−3b)y+a−8b=0,a,b∈R, which is farthest from the point (2,2), then area enclosed by the line L and the coordinate axes is
02:59View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
01:14View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
03:35View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
03:02View SolutionABCD is a square A≡(1,2),B≡(3,−4). If line CD passes through (3,8), then the midpoint of CD is (a) (2,6) (b) (6,2) (c) (2,5) (d) (285,15)
05:12View SolutionIf a+1=b+2=c+3=d+4=a+b+c+d+5, then (a+b+c+d) is equal to
04:37View SolutionIf points A(5, p), B(1, 5), C(2, 1) and D(6, 2) form a square ABCD , then p= (a) 7 (b) 3 (c) 6 (d) 8
03:00View SolutionFind the values of a,b,c and d, if 3[abcd]=[a6−12d]+[4a+bc+d3].
View SolutionFind the values of a,b,c and d, if 3[abcd]=[a6−12d]+[4a+bc+d3].
07:47View SolutionABCD is a square A≡(1,2),B≡(3,−4). If line CD passes through (3,8), then the midpoint of CD is (a) (2, 6) (b) (6,2) (c) (2,5) (d) (285,15)
01:45View SolutionIf points A(5, p), B(1, 5), C(2, 1) and D(6, 2) form a square ABCD , then p= (a) 7 (b) 3 (c) 6 (d) 8
02:41View SolutionFind the values of a,b ,c and d, if
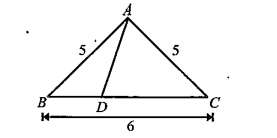
3[abcd]=[a6−12d]+[4a+bc+d3]03:41View SolutionFigure shows triangle ABC such that AB=AC=5,BC=6.P∮DisonB Csuchtˆ(B D)/(D C)=1/2,then□of≤n>hofsA D is
 02:30View Solution
02:30View SolutionABCD is a square A≡(1,2),B≡(3,−4). If line CD passes through (3,8), then the midpoint of CD is
01:09View Solution

