A car has two wipers which do not overlap. Each wiper has a blade of length 25 cm sweeping through an angle of 115o . Find the total area cleaned at each sweep of the blades.
To find the total area cleaned by the two wipers of a car, we can follow these steps:
Step 1: Understand the Problem
We have two wipers, each with a blade length of 25 cm, sweeping through an angle of 115 degrees. We need to calculate the total area cleaned by both wipers.
Step 2: Calculate the Area Cleaned by One Wiper
The area cleaned by one wiper can be calculated using the formula for the area of a sector of a circle:
Area of sector=θ360×πr2
where:
- θ is the angle in degrees,
- r is the length of the wiper blade.
Step 3: Substitute the Values
For one wiper:
- θ=115∘
- r=25 cm
Substituting these values into the formula:
Area of sector=115360×π×(25)2
Step 4: Calculate the Area of the Sector
Now, we calculate (25)2:
(25)2=625
Now, substituting this back into the area formula:
Area of sector=115360×π×625
Using π≈227:
Area of sector=115360×227×625
Step 5: Simplify the Expression
Calculating the fraction:
Area of sector=115×22×625360×7
Calculating the numerator:
115×22=2530
2530×625=1581250
Calculating the denominator:
360×7=2520
Now we have:
Area of sector=15812502520
Step 6: Calculate the Area of One Wiper
Now, we can simplify this fraction:
Area of sector≈626.9841 cm2
Step 7: Calculate the Total Area Cleaned by Both Wipers
Since there are two wipers and they do not overlap, the total area cleaned is:
Total Area=2×Area of one wiper
Total Area=2×626.9841≈1253.9682 cm2
Final Answer
The total area cleaned by both wipers is approximately:
Total Area≈1253.97 cm2
---
We have two wipers, each with a blade length of 25 cm, sweeping through an angle of 115 degrees. We need to calculate the total area cleaned by both wipers.
The area cleaned by one wiper can be calculated using the formula for the area of a sector of a circle:
Area of sector=θ360×πr2
where:
- θ is the angle in degrees,
- r is the length of the wiper blade.
For one wiper:
- θ=115∘
- r=25 cm
Area of sector=115360×π×(25)2
Now, we calculate (25)2:
(25)2=625
Now, substituting this back into the area formula:
Area of sector=115360×π×625
Using π≈227:
Area of sector=115360×227×625
Calculating the fraction:
Area of sector=115×22×625360×7
115×22=2530
2530×625=1581250
Calculating the denominator:
360×7=2520
Now we have:
Area of sector=15812502520
Now, we can simplify this fraction:
Area of sector≈626.9841 cm2
Since there are two wipers and they do not overlap, the total area cleaned is:
Total Area=2×Area of one wiper
Total Area=2×626.9841≈1253.9682 cm2
The total area cleaned by both wipers is approximately:
Total Area≈1253.97 cm2
Topper's Solved these Questions
Similar Questions
A car has two wipers which do not overlap. Each wiper has a blade of length 25 cm sweeping through an angle of 115∘ . Find the total area cleaned at each sweep of the blades.
View SolutionThe length of each edge of a rectangular box is l cm. Find its total surface area.
View SolutionTwo cubes each of volume 125cm3 are joined end to end together. Find the total surface area of the resulting cuboid.
View SolutionA rhombus of side 20cm has two angles of 600 each. Find the length of the diagonals.
View SolutionA line segment of length 84 cm has been divide into two parts in the ratio 4 : 3 . Find the length of each part
View SolutionTwo cubes with each side 10 cm are joined are joined end to end . Find the total surface area of the resulting cuboid.
View SolutionAn electric fan has blades of length 30cm as measured from the axis of rotation. If the fan is rotating at 1200 rpm, find the acceleration of a point on the tip of a blade.
View SolutionThrough a rectangular field of sides 90 m × 60 m , two roads are constructed which are parallel to the sides and cut each other at right angles through the centre of the field. If the width of the roads is 3 m, find the total area covered by the two roads.
View SolutionFind the area of a trapezium whose parallel sides of lengths 10cm and 15cm are at a distance of 6cm from each other. Calculate this area as (a) the sum of the areas of two triangles and one rectangle. (b) the difference of the area of a rectangle and the sum of the areas of two triangles.
View SolutionA design is made on a rectangular tile of dimensions 50 cm×70 cm as shown in figure. The design shows 8 triangle, each of sides 26 cm, 17 cm and 25 cm. Find the total area of the design and the remaining area of the tiles.
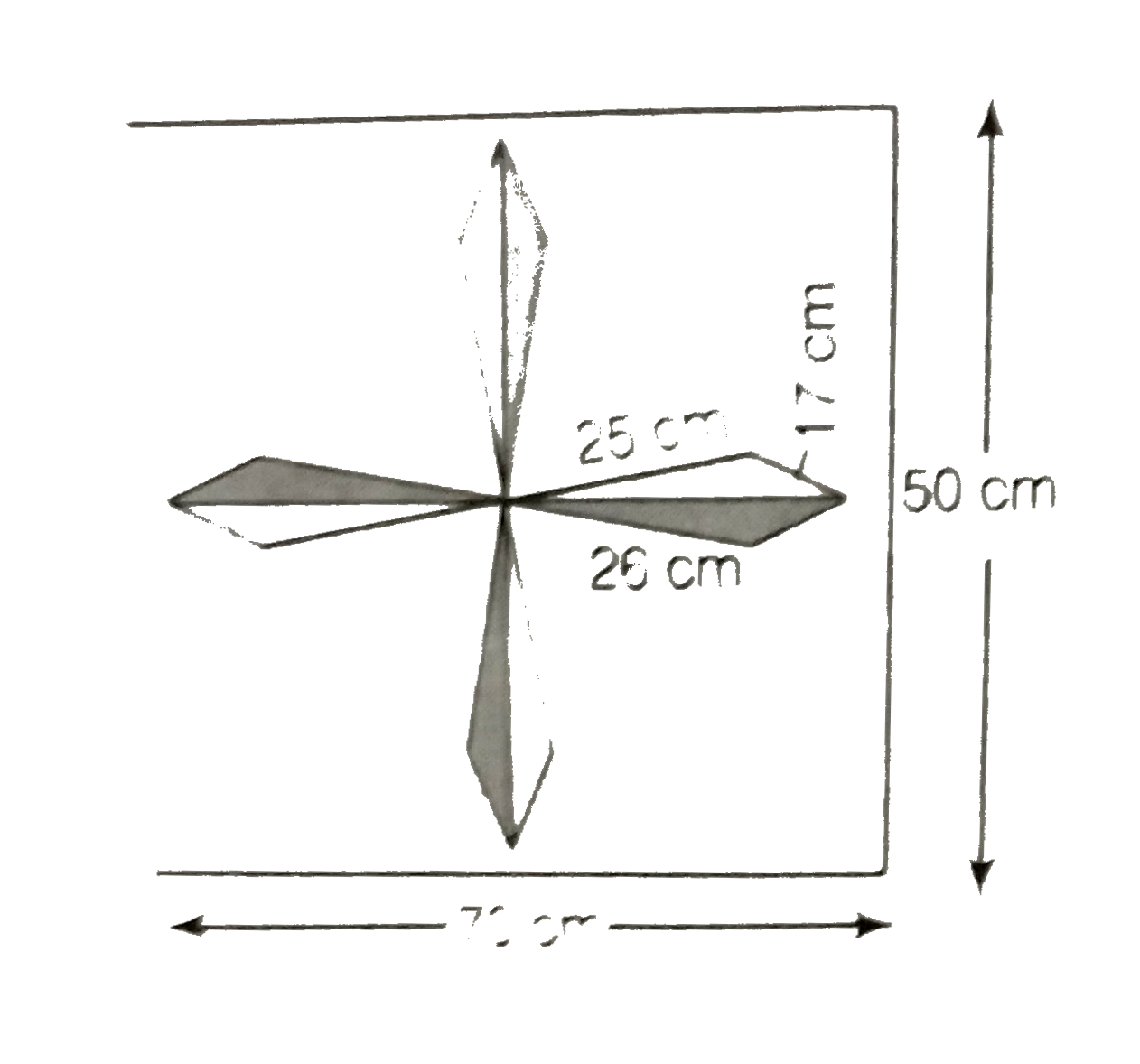 View Solution
View Solution

