A chord of length 16cm is drawn in a circle of radius 10cm. Find the distnace of the chord from the centre of the circle.
The correct Answer is:6 cm
To find the distance of the chord from the center of the circle, we can follow these steps:
Step 1: Understand the Geometry
We have a circle with a radius of 10 cm and a chord of length 16 cm. We need to find the perpendicular distance from the center of the circle to the chord.
Step 2: Draw the Diagram
Draw a circle with center O and radius 10 cm. Draw the chord AB such that its length is 16 cm. Let M be the midpoint of the chord AB. Draw a line from O to M, which is the perpendicular distance we need to find.
Step 3: Find the Length of AM
Since M is the midpoint of chord AB, we can find the length of AM:
AM=AB2=16 cm2=8 cm
Step 4: Apply the Pythagorean Theorem
In the right triangle OMA, where:
- OA is the radius (10 cm),
- AM is half the chord length (8 cm),
- OM is the distance from the center to the chord (which we need to find).
According to the Pythagorean theorem:
OA2=OM2+AM2
Substituting the known values:
102=OM2+82
100=OM2+64
Step 5: Solve for OM
Rearranging the equation to solve for OM:
OM2=100−64
OM2=36
Taking the square root of both sides:
OM=√36=6 cm
Conclusion
The distance of the chord from the center of the circle is 6 cm.
---
We have a circle with a radius of 10 cm and a chord of length 16 cm. We need to find the perpendicular distance from the center of the circle to the chord.
Draw a circle with center O and radius 10 cm. Draw the chord AB such that its length is 16 cm. Let M be the midpoint of the chord AB. Draw a line from O to M, which is the perpendicular distance we need to find.
Since M is the midpoint of chord AB, we can find the length of AM:
AM=AB2=16 cm2=8 cm
In the right triangle OMA, where:
- OA is the radius (10 cm),
- AM is half the chord length (8 cm),
- OM is the distance from the center to the chord (which we need to find).
OA2=OM2+AM2
Substituting the known values:
102=OM2+82
100=OM2+64
Rearranging the equation to solve for OM:
OM2=100−64
OM2=36
Taking the square root of both sides:
OM=√36=6 cm
The distance of the chord from the center of the circle is 6 cm.
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B
18 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12C
26 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
A chord of length 16 cm is drawn in a circle of radius 10 cm .Calculate the distance of the chord from the centre of the circle.
View SolutionThe radius of a circle with centere P is 25 cm . The length of a chord of the same circle is 48 cm . Find the distance of the chord from the centre P of the circle.
View Solution
Knowledge Check
A chord of length 16 cm is drawn in a circle of radius 10 cm .Calculate the distance of the chord from the centre of the circle.
A8 cm / सेमी०B6 cm / सेमी०C4 cm / सेमी०D12 cm / सेमी०The length of a chord of a circle of radius 10 cm is 12 cm. Find the distance of the chord from the centre of the circle.
A6 cmB5 cmC8 cmD7 cmThe length of the diameter of the circle is 10 cm and length of the chord drawn in a circle is 6 cm. Find the distance (in cm) of chord from the centre.
A10B8C6D4
(i) Find the length of a chord which is at a distance of 12 cm from the centre of a circle of radius 13cm.
(ii) The length of a chord is 16 cm of a circle of diameter 2 cm. find the perpendicular distance of this chord from the centre of the circle.
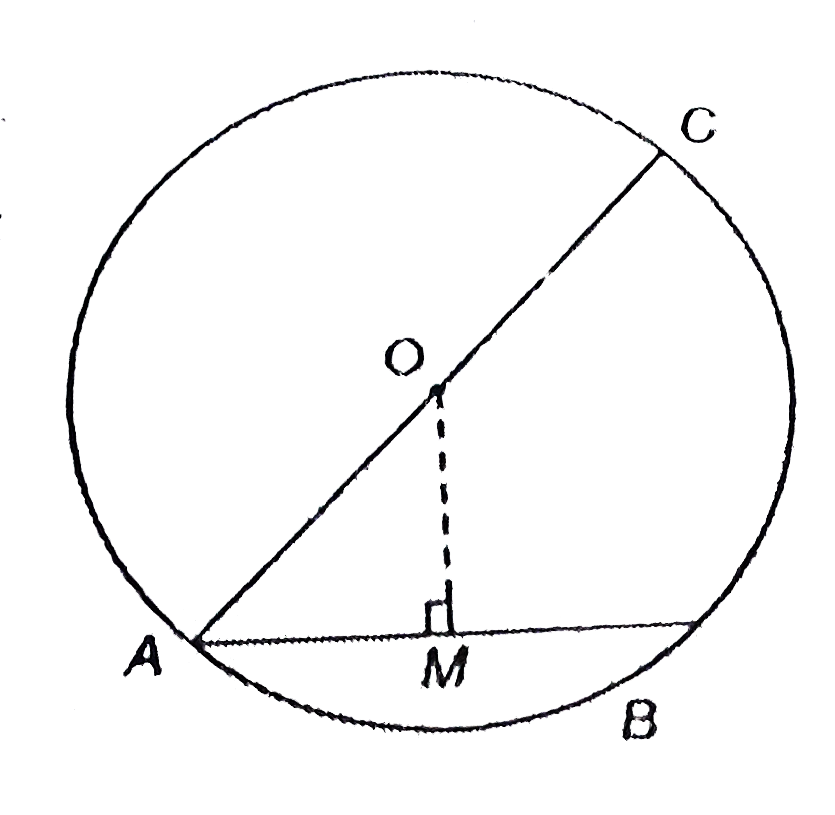
View SolutionIn the adjoining figure, O is the centre of the centre of the circle. If diameter AC=26cm and chord AB=10cm, then find the distances of the chord AB from the centre of the circle.
View SolutionThe length of the diameter of the circle is 10 cm and length of the chord drawn in a circle is 6 cm. Find the distance (in cm) of chord from the centre.
View SolutionA chord of length 10 cm subtends an angle 120∘ at the centre of a circle . Distance of the chord from the centre is
View SolutionIn a circle of radius 10 cm, a chord is at a distance of 6 cm from the centre. The length of chord is
View Solution
