An equilateral triangle of side 9 cm is inscribed in a circle. Find the radius of the circle.
The correct Answer is:3√3cm
Let ΔABC be an equilateral triangle of side 9cm. Let AD be one of its medians
Then, AD⊥BC andBD=4.5cm.
∴AD=√AB2−BD2=√(9)2−(92)2cm=9√32cm
In and equilateral triangle, the centroid and circumcentre coincide and AG:GD=2:1
∴ radius =AG23AD(23×9√32)cm=3√3cm
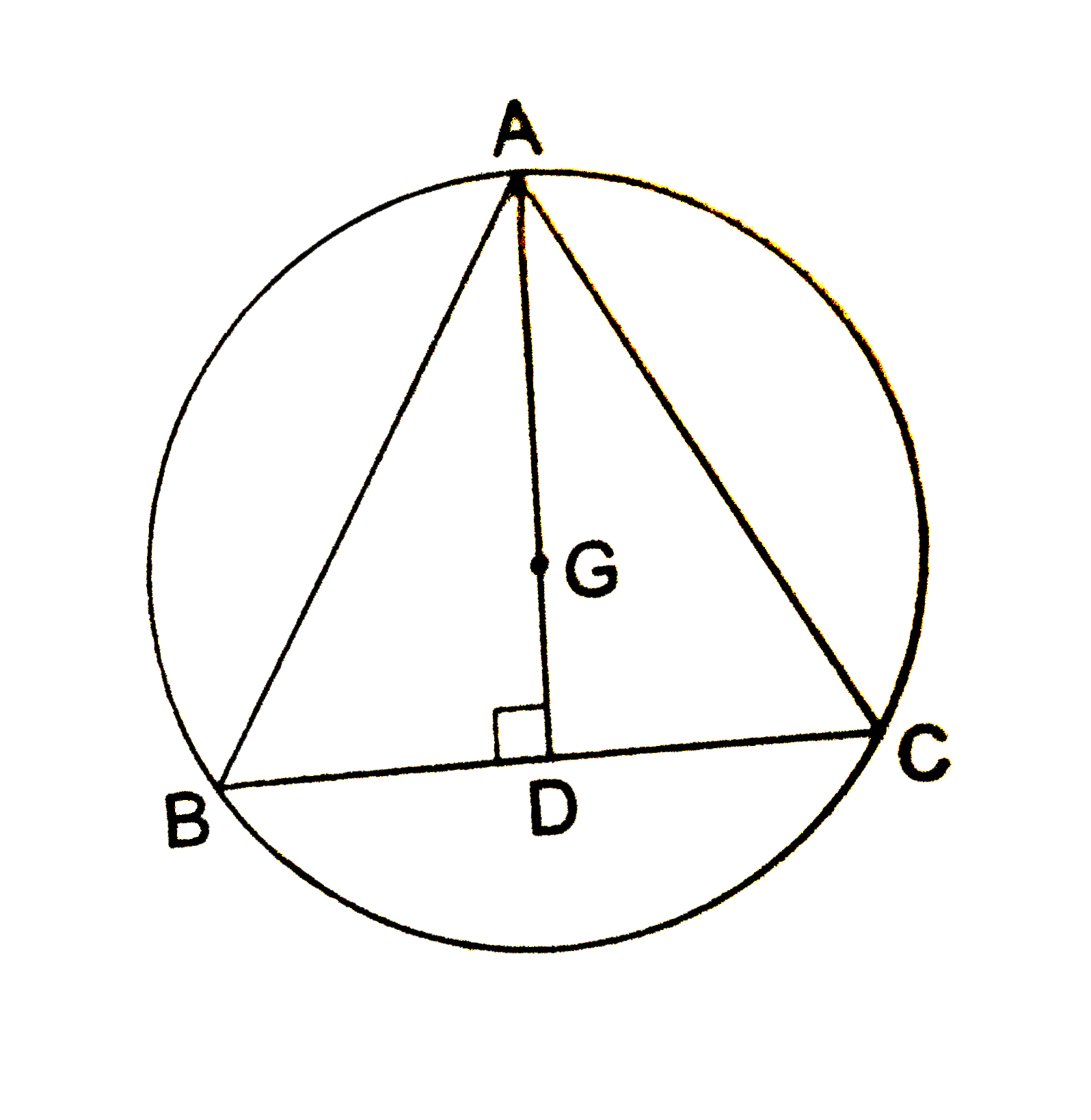
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B
18 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12C
26 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Knowledge Check
A circle is inscribed in a square. An equilateral triangle of side 4√3cm is inscribed in that circle. The length of the diagonal of the square (in centimetres) is
A4√2B8C8√2D16An equilateral triangle is inscribed in a circle of radius 6 cm. Find its side.
A6√3B6√3C8√3D2√3A circle is inscribed in an equilateral triangle and square is inscribed in that circle. The ratio of the areas of the triangle and the square is
A√3:4B√3:8C3√3:2D3√3:1
An equilateral triangle of side 6 cm is inscribed in a circle. Then radius of the circle is
View SolutionIn an equilateral triangle of side 24cm, a circle is inscribed touching its sides. Find the area of the remaining portion of the triangle (Take√3=1.732)
View SolutionIn the given figure, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region. [Use √3=1.73 and π=3.14]
View SolutionIn an equilateral triangle of side 12 cm, a circle is inscribed touching its sides. Find the area of the portion of the triangle not included in the circle. [ Take √3=1.73 abd π=3044]
View SolutionAn equilateral triangle ABC is inscribed in a circle of radius r if P be any point on the circle then find the value of PA2+PB2+PC2.
View Solution
