A circus artist is climbing from the ground along a rope stretched from the top of a vertical pole and tied at the ground. The height of the pole is 12 m and the angle made by the rope with ground level is 30∘ . Calculate the distance covered by the artist in climbing to the top of the pole.
To solve the problem step by step, we will use trigonometric ratios in a right triangle.
1. Understand the Problem:
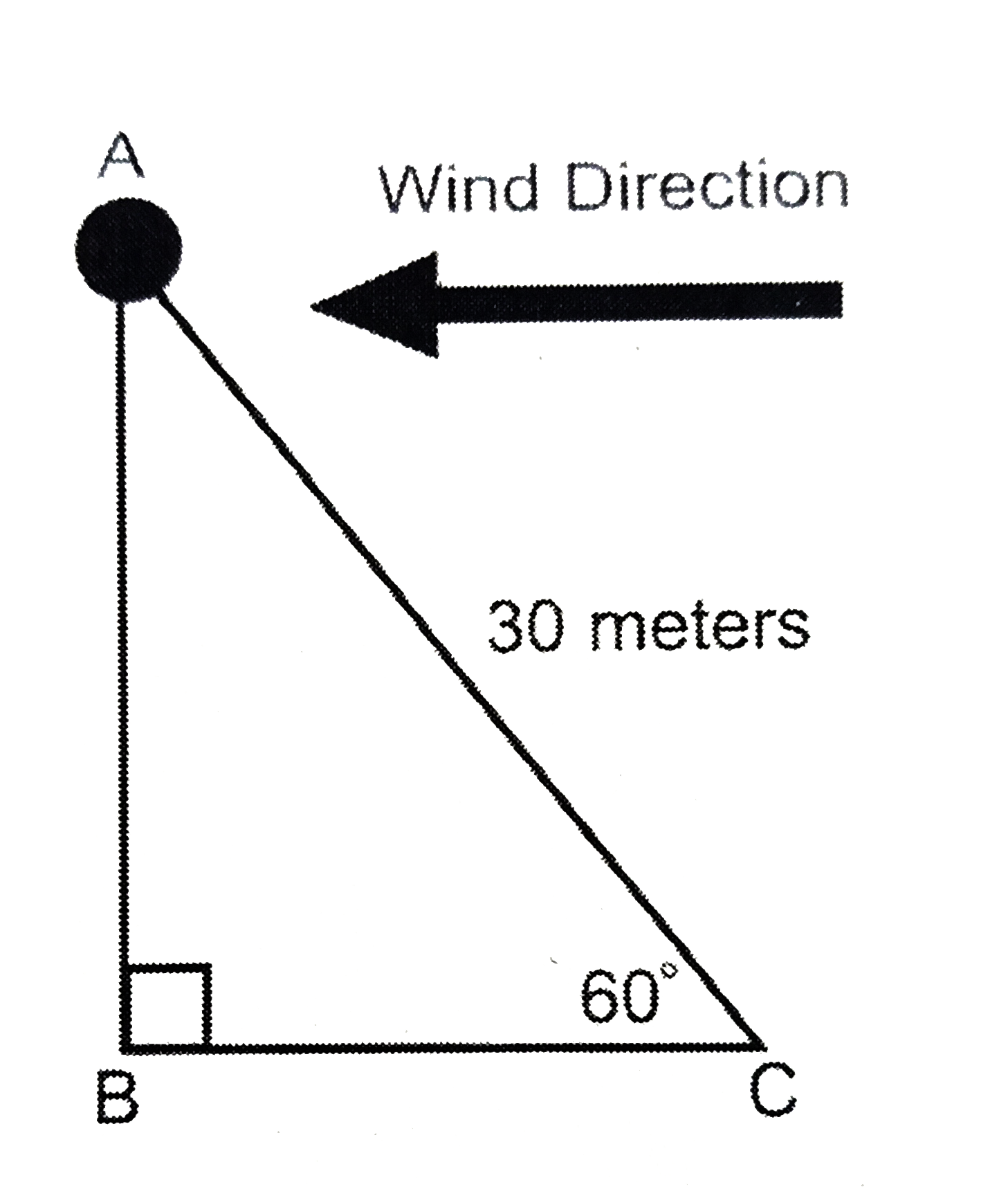
We have a vertical pole (AB) of height 12 m, and a rope (AC) stretched from the top of the pole to the ground, making an angle of 30 degrees with the ground (BC). We need to find the length of the rope AC, which represents the distance the artist climbs.
2. Draw the Diagram:
- Let A be the top of the pole.
- Let B be the bottom of the pole (ground level).
- Let C be the point where the rope meets the ground.
- The height of the pole (AB) = 12 m.
- The angle ACB = 30 degrees.
3. Identify the Right Triangle:
In triangle ABC, we have:
- AB (height of the pole) = 12 m (perpendicular)
- AC (length of the rope) = hypotenuse
- BC (distance on the ground) = base
4. Use the Sine Ratio:
Since we have a right triangle, we can use the sine function:
sin(θ)=oppositehypotenuse
Here, θ=30∘, the opposite side is AB (12 m), and the hypotenuse is AC.
5. Set Up the Equation:
sin(30∘)=ABAC
Substituting the known values:
sin(30∘)=12AC
We know that sin(30∘)=12.
6. Substitute and Solve for AC:
12=12AC
Cross-multiplying gives:
AC=2×12
AC=24 m
7. Conclusion:
The distance covered by the artist in climbing to the top of the pole is 24 meters.
We have a vertical pole (AB) of height 12 m, and a rope (AC) stretched from the top of the pole to the ground, making an angle of 30 degrees with the ground (BC). We need to find the length of the rope AC, which represents the distance the artist climbs.
- Let A be the top of the pole.
- Let B be the bottom of the pole (ground level).
- Let C be the point where the rope meets the ground.
- The height of the pole (AB) = 12 m.
- The angle ACB = 30 degrees.
In triangle ABC, we have:
- AB (height of the pole) = 12 m (perpendicular)
- AC (length of the rope) = hypotenuse
- BC (distance on the ground) = base
Since we have a right triangle, we can use the sine function:
sin(θ)=oppositehypotenuse
Here, θ=30∘, the opposite side is AB (12 m), and the hypotenuse is AC.
sin(30∘)=ABAC
Substituting the known values:
sin(30∘)=12AC
We know that sin(30∘)=12.
12=12AC
Cross-multiplying gives:
AC=2×12
AC=24 m
The distance covered by the artist in climbing to the top of the pole is 24 meters.
Topper's Solved these Questions
Similar Questions
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30∘.
View SolutionA circus artists is climbing a 20m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole if the angle made by the rope with the ground level is 300.
View Solution
Knowledge Check
- Question 1 - Select One
A hot air balloon was tied to a point on the ground using a rope 60m long. If the rope makes an angle of 60∘ with the ground, how high, in meters, is the balloon above the ground level?A30√3B30C60√3D30√3
A circus artist is climbing a 30 m rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole to the ground. Find the height of the angle made by the rope with the ground level is 30∘), as shown in the figure.
 View Solution
View SolutionA body falls freely from the top of a tower. It covers 36% of the total height in the lkast second before striking the ground level. The height of the tower is
View SolutionA pole on the ground lenses 60∘ to the vertical. At a point a meters away from the base of the pole on the ground, the two halves of the pole subtend the same angle. If the pole and the point are in the same vertical plane, the length of the pole is
View SolutionA man stands 9 m away from a flag-pole. He observes that angle of elevation of the top of the pole is 28∘ and the angle of depression of the bottom of the pole is 13∘ .Calculate the height of the pole .
View Solution5 m high pole stands on a building of height 25 m. The pole and the building subtend equal angles at an antenna placed at a height of 30 m. The distanceo f the antenna from the top of the pole is
View SolutionThe angle of elevation of the top of a vertical tower PQ from a point X on the ground is 60o . At a point Y , 40m vertically above X , the angle of elevation of the top is 45o . Calculate the height of the tower.
View SolutionThe angle of elevation of the top of a vertical tower PQ from a point X on the ground is 60o . At a point Y , 40m vertically above X , the angle of elevation of the top is 45o . Calculate the height of the tower.
View Solution

