A discrete random variable has the probability distribution given below: Find the value of (ii) Determine the mean of the distribution.
To solve the given problem, we will follow these steps:
Step 1: Write down the probability distribution
The random variable X and its corresponding probabilities are given as follows:
X:0.511.52P(X):kk22k2k
Step 2: Set up the equation for the total probability
Since the sum of all probabilities must equal 1, we can write the equation:
k+k2+2k2+k=1
Step 3: Simplify the equation
Combine like terms:
k+3k2=1
Rearranging gives us:
3k2+k−1=0
Step 4: Solve the quadratic equation
Now, we will solve the quadratic equation 3k2+k−1=0 using the quadratic formula:
k=−b±√b2−4ac2a
Here, a=3, b=1, and c=−1.
Calculating the discriminant:
b2−4ac=12−4⋅3⋅(−1)=1+12=13
Now substituting into the quadratic formula:
k=−1±√132⋅3=−1±√136
Step 5: Determine valid values for k
Calculating the two possible values for k:
1. k=−1+√136
2. k=−1−√136
Since probabilities cannot be negative, we discard the second solution. We will approximate the first solution:
k≈−1+3.60556≈2.60556≈0.43425
Step 6: Calculate the mean of the distribution
The mean μ of the distribution can be calculated using the formula:
μ=∑(xi⋅P(Xi))
Substituting the values:
μ=(0.5⋅k)+(1⋅k2)+(1.5⋅2k2)+(2⋅k)
Substituting k≈0.43425:
μ=(0.5⋅0.43425)+(1⋅(0.43425)2)+(1.5⋅2(0.43425)2)+(2⋅0.43425)
Calculating each term:
1. 0.5⋅0.43425≈0.217125
2. 1⋅(0.43425)2≈0.188
3. 1.5⋅2(0.43425)2≈0.564
4. 2⋅0.43425≈0.8685
Adding these values together:
μ≈0.217125+0.188+0.564+0.8685≈1.837625
Final Answers
1. The value of k is approximately 0.43425.
2. The mean of the distribution is approximately 1.837625.
2. k=−1−√136
2. 1⋅(0.43425)2≈0.188
3. 1.5⋅2(0.43425)2≈0.564
4. 2⋅0.43425≈0.8685
2. The mean of the distribution is approximately 1.837625.
Topper's Solved these Questions
Similar Questions
A random variable X has the following distribution

View SolutionA discrete random variable X has the probability distribution as given below
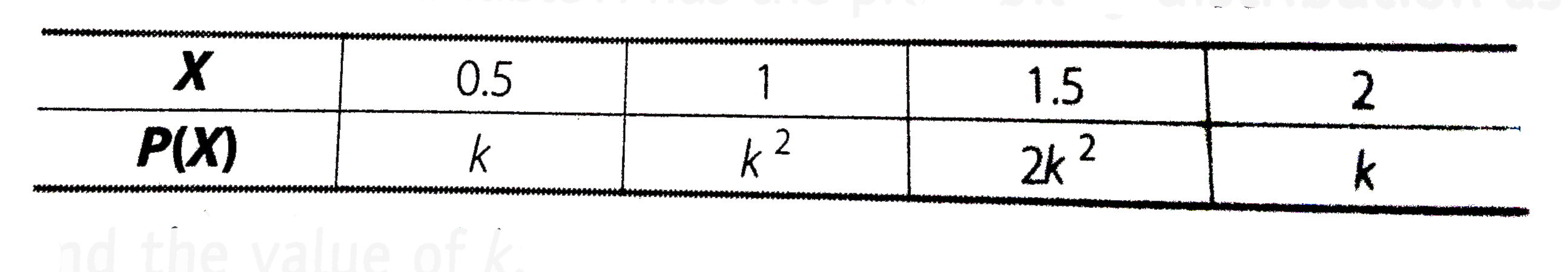
(i) Find the value of k.
(ii) Determine the mean of the distribution.
View SolutionA discrete random variable X has the probability distribution as given below
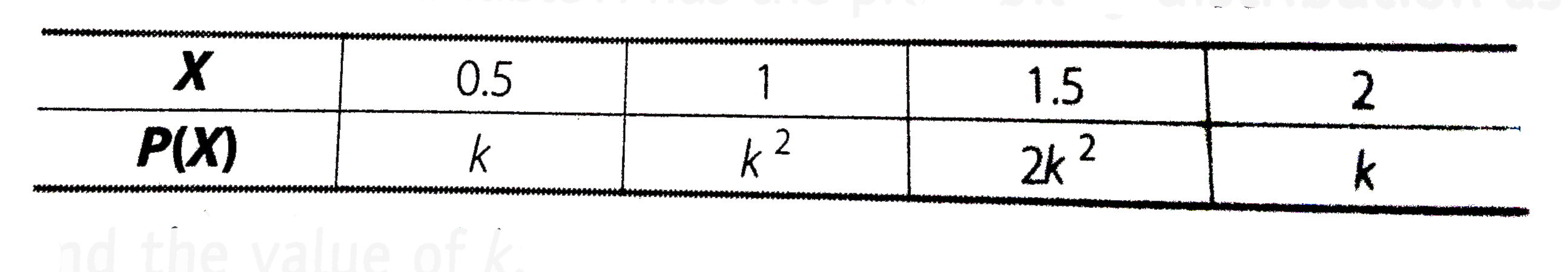
(i) Find the value of k.
(ii) Determine the mean of the distribution.
View SolutionA discrete random variable X has the probability distribution given below: X: 0.5 1 1.5 2 P(X): k k2 2k2 k then, Find the value of k.
View SolutionA discret random variable X has the following probability distribution: X:1234567 P(X):c2c2c3^22c27c2+c Find the value of ⋅ Also, find the mean of the distribution.
View SolutionA random variable 'X' has the following probability distribution :

The values of k is
View SolutionA random variable X has the following probability distribution :

determine the value of a
View SolutionA random variable X as the following probability distribution: xi:−2−10123 pi:0.1k0.22k0.3k Find (i) Find the value of k. (ii) Calculate the mean ofX. Calculate the variance of X.
View SolutionA random variable X as the following probability distribution: xi:−2−10123 pi:0.1k0.22k0.3k Find (i) Find the value of k. (ii) Calculate the mean ofX. Calculate the variance of X.
View SolutionA random variable X has the following distribution
x:1234P(X=x):k23k25k27k2
The value of k is
View Solution
